S
SỞ
ỞG
GD
D&
&Đ
ĐT
TQUẢ
QUẢN
NG
GTRỊ
TRỊ
T
TR
RƯỜ
ƯỜN
NG
GT
TH
HP
PT
TL
LÊ
ÊL
LỢ
ỢI
I ĐỀ
ĐỀT
TH
HI
IT
TH
HỬ
ỬĐ
ĐẠ
ẠI
IHỌ
HỌC
CM
MÔ
ÔN
NTOÁ
TOÁN
NK
KH
HỐ
ỐI
IA
AL
LẦ
ẦN
NT
TH
HỨ
Ứ1
1
N
NĂ
ĂM
MHỌ
HỌC
C2
20
01
10
0–
–2
20
01
11
1
T
Th
hờ
ời
ig
gi
ia
an
n1
18
80
0phú
phút
t
I
I.
.P
PH
HẦ
ẦN
NC
CH
HU
UN
NG
GC
CH
HO
OT
TẤ
ẤT
TCẢCÁ
CẢCÁC
CTHÍ
THÍS
SI
IN
NH
H(
(7
7đ
đi
iể
ểm
m)
)
CâuI.(2,0điểm) Chohàmsố 1
= -
x
y xcóđồthị (C)
1. Khảosátsựbiếnthiênvàvẽđồthị (C)củahàmsốđãcho.
2. Tìmcácgiátrịcủamđể đườngthẳng =- +y x m cắtđồthị (C)tạihaiđiểmphânbiệtAvàBsaocho
gócgiữahaiđườngthẳngOAvàOBbằng 0
60 (với Olàgốc tọađộ).
CâuII.(2,0 điểm)
1. Giải phươngtrình:
( )
2
2 3 .cos 2sin 2 4 1
2cos 1
p
æ ö
- - -
ç ÷
è ø =
-
x
x
x.
2. Giảibấtphươngtrình:
( )
2 2
2 . 1 4x x x - - £ - .
CâuIII.(1,0điểm) Tínhtíchphân
7
2
1
3 2 2
+
= + + -
òx
I dx
x x.
CâuIV.(1,0 điểm)
Cho hình lập phương / / / /
.ABCD A B C D có cạnh bằng a. M là điểm thuộc cạnh CD với
( )
0 = < <CM x x a,Nlàtrungđiểmcạnh / /
A D . Tínhtheoa thểtích củakhốitứdiện / /
B MC N.Xác
định xđể haiđườngthẳng /
B Mvà /
C N vuônggócvớinhau.
CâuV.(1,0điểm)
Xácđịnh các giátrịcủathamsố mđể phươngtrìnhsauđây cónghiệmthực
( )
2 2 4 2
1 1 2 1 2 + - + = - + + - +m x x x x x x .
I
II
I.
.P
PH
HẦ
ẦN
NR
RI
IÊ
ÊN
NG
G(
(3
3đ
đi
iể
ểm
m)
) Chúý
Chúý.
.Thí
Thís
si
in
nh
hchỉ
chỉđ
đượ
ược
cc
ch
họ
ọn
nm
mộ
ột
tt
tr
ro
on
ng
gh
ha
ai
ip
ph
hầ
ần
n(
(p
ph
hầ
ần
n1
1h
ho
oặ
ặc
cp
ph
hầ
ần
n2
2)
)
1.Theochương trìnhChuẩn.
CâuVI.a(2,0 điểm)
1. TrongmặtphẳngtọađộOxy,chotamgiácABC có
( )
1;2MlàtrungđiểmcạnhBCcònhaicạnhABvà
AClầnlượtcó phươngtrình 2 2 0 - - =x y và 4 1 0 + - =x y . Tìm tọađộcácđỉnh củatam giácđó.
2. Trong không gian tọa độ Oxyz, cho
( ) ( ) ( )
2;1;0 , 0; 5;0 , 1; 2;6A B C - -và mp(P): 4 0 + + - =x y z .
Tìmtọađộtrọngtâm Gcủatam giácABC. Tìmđiểm Ithuộcmp(P)saocho + +
uur uur uur
IA IB ICnhỏnhất.
CâuVII.a(1,0 điểm)
Giảihệphươngtrìnhsautrongtậphợp cácsốphức: 2 3 1
2
ì - =- +
ï
ï
í
ï- + = +
ï
î
x y i
x iy i.
2.TheochươngtrìnhNângcao.
CâuVI.b(2,0 điểm)
1. Trong mặt phẳng tọa độ Oxy cho đường tròn
( )
2 2
: 2 + =C x y. Viết phương trình tiếp tuyến của
đườngtròn(C)biếttiếptuyếnđócắtcáctiaOx,OylầnlượttạiAvàBsaochotamgiácOABcódiện
tích nhỏnhất.
2. TrongkhônggiantọađộOxyz,viếtphươngtrìnhmặtphẳng(P)chứatrụcOyvà(P)cắtmặtcầu(S):
2 2 2 2 6 4 5 0 + + - + - + =x y z x y z theogiaotuyến làmộtđườngtròn cóbán kínhbằng2.
CâuVII.b(1,0 điểm)
Giảihệ phươngtrình
2 2
ln 2ln 6 ln 2ln 6 ln ln
3 2 5
ì
ï + + - + + = -
ï
ï
í
ï + =
ï
ï
îx y
x x y y x yvới , . Î ¡x y
–––––––HẾT––––––––
Ghi chú. HSkhôngđược dùngtàiliệuvàGiám thị không giải thích gì thêm.
Họvà tên thí sinh:…………………………Sốbáodanh:……………………
www.laisac.page.tl
ĐÁP ÁN–THANGĐIỂM ĐỀTHITHỬ ĐẠIHỌC
MÔN TOÁNKHỐIALẦNTHỨNHẤT
CÂU Ý ĐÁP ÁN Điểm
+TXĐ:
{ }
\ 1¡
+Sự biếnthiên:
–Chiềubiến thiên:
( )
2
1
' 0, 1
1
y x
x
= - < " ¹
-,y’khôngxácđịnhtại 1x =.
0,25
– Hàmsốnghịchbiếntrên cáckhoảng
( )
;1 -¥và
( )
1;+¥, hàmsốkhôngcó cực trị.
–Giớihạn vàtiệmcận: lim lim 1
x x
y y
®-¥ ®+¥
= = Þtiệmcậnngang 1y = .
1 1
lim ; lim
x x
y y
+ -
® ®
= +¥ =-¥ Þtiệmcậnđứng 1x =.
0,25
– Bảngbiếnthiên:
x 1 -¥ +¥
y'|| - -
y1 +¥
-¥1
0,25
1
(1,0
điểm)
+Đồthị:
– Đồthị cắtOy tại
( )
0;0O
– Đồthị cắtOx tại
( )
0;0O
– Tâmđốixứnglàđiểm
( )
1;1I.
0,25
+PT hoànhđộgiaođiểm 2
( ) 0
1
x x m g x x mx m
x = - + Û = - + =
-(1) với 1x ¹. 0,25
+Đườngthẳng y x m =- + cắtđồthị (C)tạihaiđiểmphânbiệt
ÛPhươngtrình (1) cóhainghiệmphânbiệt 1x ¹
2 0 4
4 0 0 4 (*)
1 0
(1) 0
hoaëc hoaëc
m m
m m m m
g
ì ì < >
ïD = - > ï
ï ï
Û Û Û < >
í í
ï ï ¹
¹ ï
î ï
î
.
0,25
I
(2,0
điểm)
2
(1,0
điểm)
+Gọi 1 2
;x x làhainghiệmcủa(1),tacó
( ) ( )
1 2
1 2
1 2
.
0
x x m
x x m
g x g x
ì
ï + =
ï
ï
ï =
í
ï
ï
ï = =
ï
î
(**)
+Cácgiaođiểmlà
( ) ( )
1 1 2 2
; , ;A x x m B x x m - + - +và
( )
( )
1 1
2 2
;
;
OA x x m
OB x x m
ì
ï = - +
ï
ï
í
ï = - +
ï
ï
î
uuur
uuur
0,25
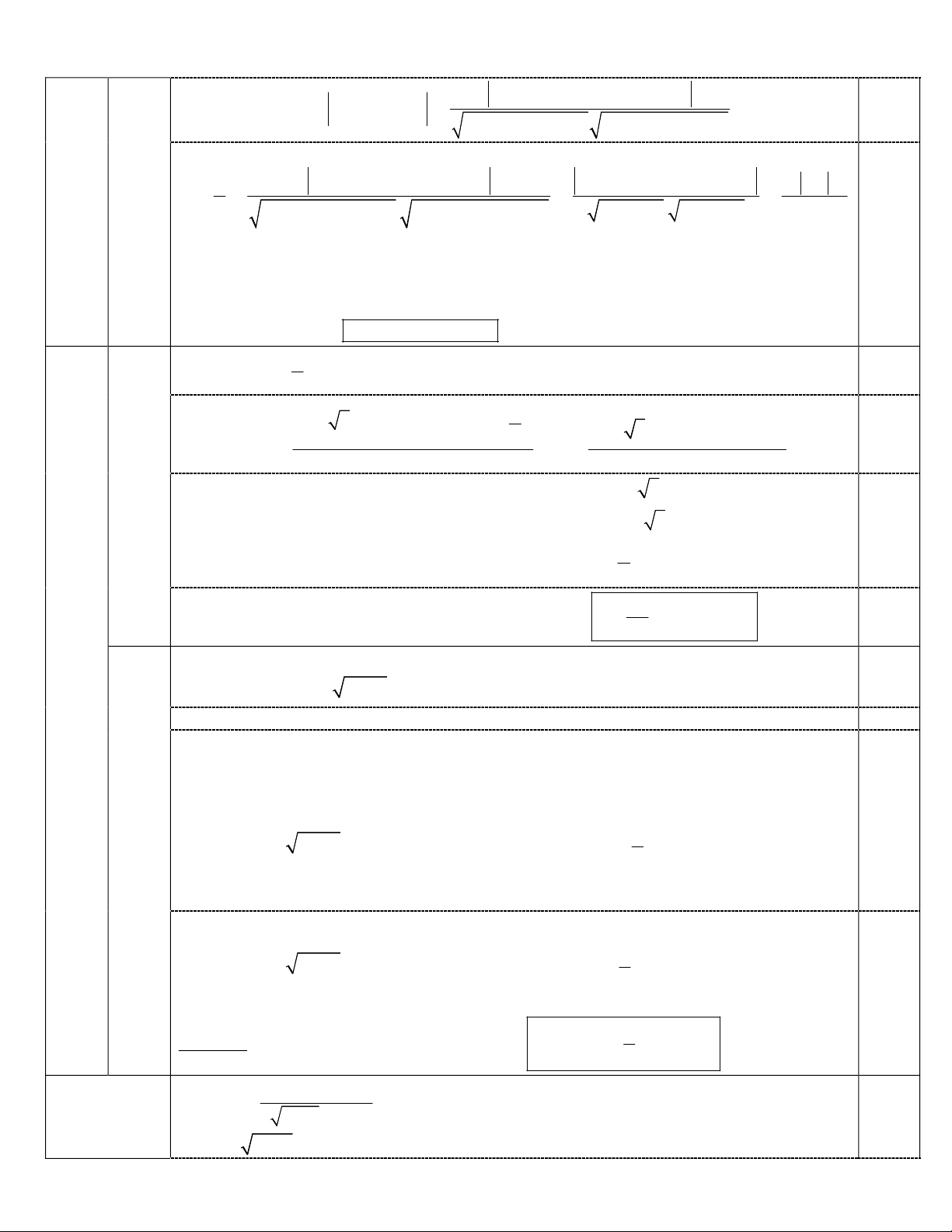
+Khiđó
( )
( )( )
1 2 1 2
0
2 2 2 2
1 1 2 2
cos60 cos , 2 2 2 2
x x x m x m
OA OB x mx m x mx m
+ - + - +
= = - + - +
uuur uuur
( )
( ) ( )
( )
2 2
1 2 1 2 1 2 1 2
2
2 2 2 2
1 2
2 2 2
1
2 2
2 2 . 2 2 2 . 2
x x m x x m x x m x x m m
m m
g x m m g x m m m m m m
- + + - + +
Û = = = -
+ - + - - -
(do(**))
{ }
2
2
2 4 2;0;6
2 4
m m m m
m m m
é - =
ê
Û Û Î -
ê - = -
ê
ë
Kếthợpvới(*)tacó 2 6 hoaëcm m = - =.
0,25
+ĐK: 1
cos 2
x¹0,25
+Tacó
( ) ( )
( )
2 3 .cos 1 cos 2 3 .cos 1 sin
2 1 1
2cos 1 2cos 1
PT
x x x x
x x
p
é ù
æ ö
÷
ç
ê ú
- - - - ÷
ç ÷ - - -
ç
ê ú
è ø
ë û
Û = Û =
- -
0,25
sin 3 cos 0
tan 3
, .
3
x x
x
x k k
p p
Þ - =
Û =
Û = + Î ¢
0,25
1
(1,0
điểm)
+Kếthợpđiềukiện,tacónghiệmcủaphươngtrìnhlà 4 2 ,
3
x m m
p p = + Î ¢. 0,25
ĐK: 2 1 0 1 1 hoaëcx x x - ³ Û £- ³
Tacó
( ) ( ) ( )
2
2 . 1 2 . 2 (1) PT x x x x Û - - £ - +0,25
TH1.Xét 2x =,PT(1)thỏamãn. 0,25
TH2.Xét
( ] [ )
; 1 1;2x Î -¥ - È
( )
2
2
2
2
2 0
1 0 5
1 2 2 0 4
1 2
(1) (thoûa ñieàu kieän ñang xeùt)
x
x
x x x
x
x x
éì + £
ï
ï
ê
í
êï - ³
ï
î
ê
Û - ³ + Û Û £-
ê
ì + >
ï
ê
ï
êí
êï - ³ +
ï
î
ë
0,25
II
(2,0
điểm)
2
(1,0
điểm)
TH3.Xét
( )
2;x Î +¥
( )
2
2 2 5
1 2 1 2 4
(1) x x x x x Û - £ + Û - £ + Û ³-
Sosánhđiềukiệnđangxét,nghiệmcủa(1)trongTH3là 2x >.
Kếtluận.Tậpnghiệmcủabấtphươngtrìnhlà
[ )
5
; 2;
4
S æ ù
ç ú
= -¥ - È +¥
ç
ç ú
è û.
0,25
III
(1,0 điểm)
Tính
7
2
1
3 2 2
+
= + + -
òx
I dx
x x
Đặt 2
2 2t x x t = + Þ = - và 2dx tdt =0,25
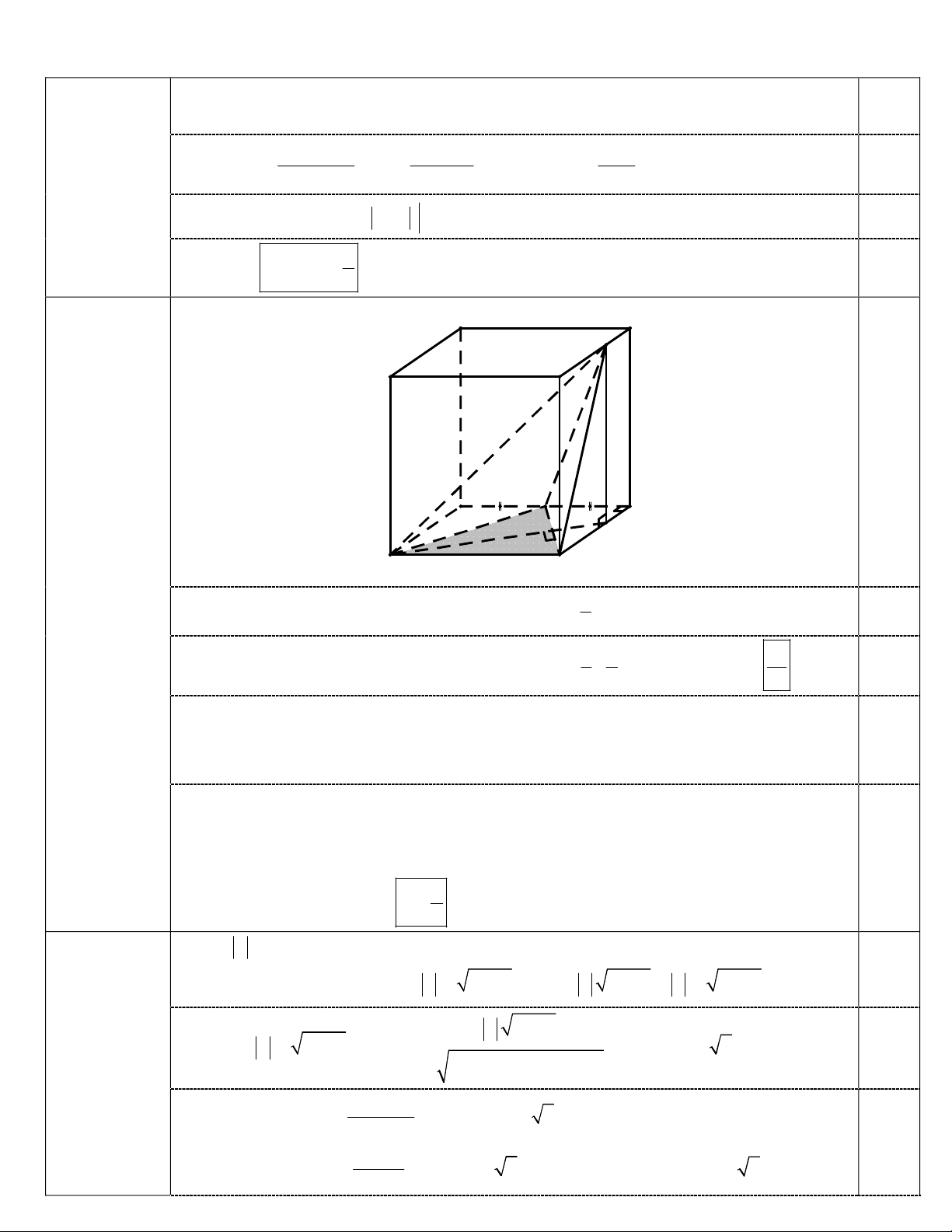
Đổicận: 2 2
7 3
x t
x t
ì = Þ =
ï
ï
í
ï = Þ =
ï
î
Tacó
( )
( )
2
3 3 3
2
2 2 2
1 .2 2 1 24
2 6
3 4 4 4
t t t t
I dt dt t dt
t t t t
- æ ö + ÷
ç
= = = - + ÷
ç ÷
ç
è ø
+ - + +
ò ò ò0,25
( )
3
2
2
6 24ln 4t t t = - + + 0,25
7
1 24ln6
= - +. 0,25
H
N
D
C
A
A'
B'
C'
D'
B
M
*Tínhthểtíchtứdiện B’MC'N:
( )
( )
' ' . ' ' ' '
1 . , ' ' ' '
3
B MC N M B C N B C N
V V S d M A B C D
D
= =0,25
3
1 1
. ' '. ' ' . '
3 2 6
a
A B B C AA
æ ö
÷
ç
= =
÷
ç ÷
ç
è ø0,25
*Tìm xđểB’M ^ C’N
Gọi HlàhìnhchiếuvuônggóccủaM trên(A’B’C’).
ÞB’HlàhìnhchiếuvuônggóccủaB’M trên(A’B’C’).
Vậy ' ' ' 'B M C N B H C N ^ Û ^
0,25
IV
(1,0 điểm)
·
·
' ' ' '
' ' ' '
' '
.
2
C B H D C N
B C H C D N
C H D N
a
x
Û =
Û D =D
Û =
Û =
0,25
+ĐK: 1x £
Phươngtrìnhtươngđương
( )
2 2 2
1 1 2 1 1 2m x x x x x x + - + = - + + - + (2) 0,25
+Đặt
( )( )
2 2
2
2 2 2 2
1 2 1
1 0 .
1 1 1
t x x
t x x t x x
ì
ï = + -
ï
ï
= + - ³ Þ í
ï £ + + -
ï
ï
î
Vậy1 2t £ £0,25
V
(1,0 điểm)
+Tacó
( ) ( )
2 1
2 1
t t
f t m
t
+ +
Û = =
+với 1; 2t é ù
Î ê ú
ë û
( )
2
/ 2 0, 1; 2
1
t t
f t t
t
+ é ù
Þ = > " Î ê ú
ë û
+nên
( )
f tđồngbiếntrên 1; 2
é ù
ê ú
ë û.
0,25
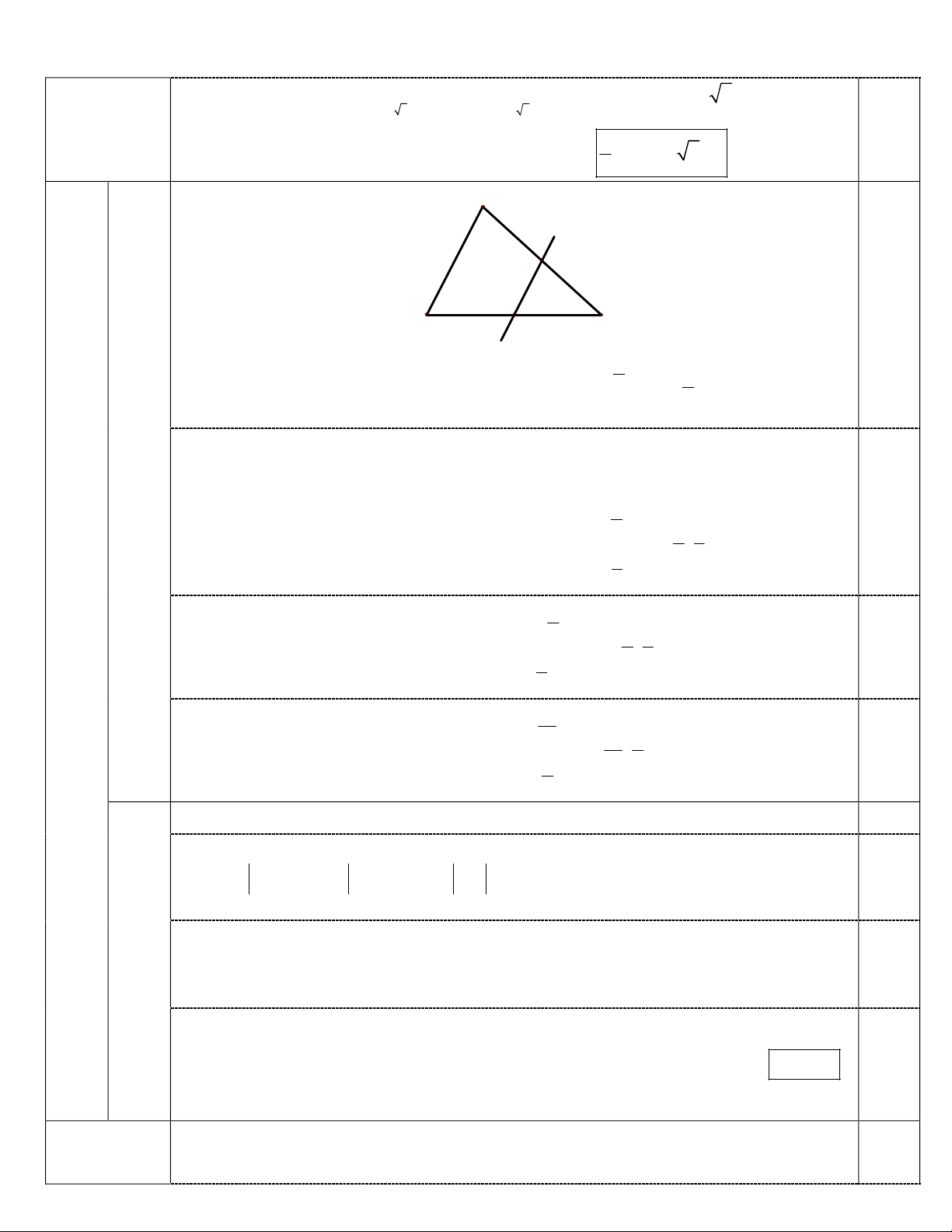
+PTđãchocónghiệm
( ) ( ) ( )
( )
1; 2 1; 2
min max 1 2f t m f t f m f
é ù é ù
ê ú ê ú
ë û ë û
Û £ £ Û £ £
3 2 2 1
2m Û £ £ - .
0,25
N
M
A
B
C
+Tọađộ củaAlànghiệmcủahệ
1
2 2 0 1; 1
2
4 1 0 2
1
x y x A
x y y
ì
ï
ì ï
- - = æ ö
=
ï ï
ï ÷
ç
Û Þ - ÷
í í ç ÷
ç
ï ï è ø
+ - =
ï
î ï =-
ï
î
0,25
+Gọi Nlàtrungđiểm ACthì MNsongsongABnên
( )
2; 1
MN AB
n n = = -
uuur uuur
Suyraphươngtrình MN:
( ) ( )( )
2 1 1 2 0 2 0x y x y - + - - = Û - =
Tọađộ củaNlànghiệmcủahệ
1
2 0 1 1
6 ;
4 1 0 1 6 3
3
x
x y N
x y y
ì
ï
ï =
ï
ì - = æ ö
ï ï
ï ï ÷
ç
Û Þ ÷
í í ç ÷
ç
ï ï è ø
+ - =
ï
î ï =
ï
ï
ï
î
.
0,25
+Nlàtrungđiểm ACsuyra
1
2 1 5
6 ;
5 6 3
2 3
C N A
C N A
x x x
C
y y y
ì
ï
ï = - = -
ï æ ö
ï
ï ÷
ç
Þ - ÷
í ç ÷
ç
ï è ø
ï = - =
ï
ï
ï
î
. 0,25
1
(1,0
điểm)
+Mlàtrungđiểm BCsuyra
13
2 13 7
6 ;
7 6 3
2 3
B M C
B M C
x x x
B
y y y
ì
ï
ï = - =
ï æ ö
ï
ï ÷
ç
Þ ÷
í ç ÷
ç
ï è ø
ï = - =
ï
ï
ï
î
. 0,25
+Trọngtâm Gcủatam giácABC:
( )
1; 2;2G -0,25
+Tacó 3IA IB IC IG + + =
uur uur uur uur
SuyraIA IB IC + +
uur uur uurnhỏnhất 3IG Û uurnhỏnhấtIG Ûnhỏnhất
I ÛlàhìnhchiếuvuônggóccủaGtrên(P)
0,25
+ĐườngthẳngdquaG,vuông gócvới (P)cóphươngtrình
1
2
2
x t
y t
z t
ì = +
ï
ï
ï
ï =- +
í
ï
ï = +
ï
ï
î
0,25
VIa
(2,0
điểm)
2
(1,0
điểm)
+Tọađộ Mlànghiệmcủahệ
1 2
2 1
2 3
4 0
x t x
y t y
z t z
x y z
ì = +
ï
ï ì =
ï
ï ï
ï = - + ï
ï ï
Þ =-
í í
ï ï
= +
ï ï =
ï ï
ï
î
ï + + - =
ï
î
.Hay tọađộMlà
( )
2; 1;3 -. 0,25
VIIa
(1,0 điểm)+Tacó
( )
2
2 3 1 2 3 1
3 2 3 32 2 2 4 2
x iy i
x y i x y i
i y ix iy i x iy i
ì
ì ì - + = +
ï
- = - + - = - +
ï ï
ï ï ï
Û Û
í í í
ï ï ï - + = + - + = + - + = +
ï ï
î î ï
î0,25
![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)
![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)
