S GIÁO D C VÀ ĐÀO T O Đ K L KỞ Ụ Ạ Ắ Ắ
TR NG THPT NGUY N HUƯỜ Ễ Ệ Đ THI TH Đ I H C Ề Ử Ạ Ọ
MÔN TOÁN NĂM 2012 - 2013
I. PH N CHUNG CHO T T C CÁC THÍ SINH (7 đi m)Ầ Ấ Ả ể
Câu I (2 đi m)ể Cho hàm s ố
( )
33 2 m
y x mx C= − +
1. Kh o sát s bi n thiên và v đ th c a hàm s ả ự ế ẽ ồ ị ủ ố
( )
1
C
2. Tìm m đ đ ng th ng đi qua đi m c c đ i, c c ti u c aể ườ ẳ ể ự ạ ự ể ủ
( )
m
C
c t đ ng tròn tâm ắ ườ
( )
1;1 ,I
bán kính b ng 1 t i hai đi m phân bi t ằ ạ ể ệ A, B sao cho di n tích tam giác ệIAB đ t giá tr l n nh tạ ị ớ ấ
Câu II (2 đi m)ể
1. Gi i ph ng trình ả ươ
( )
2
2cos3 cos 3 1 sin 2 2 3 os 2 4
x x x c x
π
� �
+ + = +
� �
� �
2. Gi i ph ng trình ả ươ
( )
2
2 2
1 5 2 4x x x+ = − +
Câu III (1 đi m) ểTính tích phân
∫
+
+
=
e
dxxx
xx
x
I
1
2ln3
ln1
ln
Câu IV (1 đi m) ểCho hình chóp S.ABC có đáy ABC là tam giác vuông cân đ nh A, ỉ
. G i I là trung đi mọ ể
c a c nh BC. Hình chi u vuông góc H c a S lên m t ph ng (ABC) th a mãn ủ ạ ế ủ ặ ẳ ỏ
2IA IH= −
uur uuur
. Góc gi a SC và m t đáyữ ặ
(ABC) b ng ằ
0
60
. Hãy tính th tích kh i chóp S.ABC và kho ng cách t trung đi m K c a SB đ n m t ph ng (SAH).ể ố ả ừ ể ủ ế ặ ẳ
Câu V (1 đi m) ểCho 3 s th c d ng a, b, c th a mãn ố ự ươ ỏ
2 2 2 1abc+ + =
.
Ch ng minh r ng ứ ằ
5 3 5 3 5 3
2 2 2 2 2 2
2 2 2 2 3
3
a a a b b b c c c
b c c a a b
− + − + − +
+ +
+++
II. PH N RIÊNG (3,0 đi m)Ầ ể
Thí sinh ch đ c làm m t trong hai ph n A ho c Bỉ ượ ộ ầ ặ
A. Theo ch ng trình chu nươ ẩ
Câu VI.a (2,0 đi m)ể
1. Trong m t ph ng v i h tr c t a đ ặ ẳ ớ ệ ụ ọ ộ Oxy cho hình ch nh t ABCD có di n tích b ng 12, tâm I là giao đi mữ ậ ệ ằ ể
c a đ ng th ng ủ ườ ẳ
: 3 0d x y− − =
và
': 6 0d x y+ − =
. Trung đi m m t c nh là giao đi m c a ể ộ ạ ể ủ d v i tr c ớ ụ Ox. Tìm
t a đ các đ nh c a hình ch nh t.ọ ộ ỉ ủ ữ ậ
2. Trong không gian v i h tr c t a đ Oxyz cho hai đi m ớ ệ ụ ọ ộ ể
(0; 1;2)M−
và
( 1;1;3)N−
. Vi t ph ng trình m tế ươ ặ
ph ng (P) đi qua M, N sao cho kho ng cách t ẳ ả ừ
( )
0;0;2K
đ n (P) đ t giá tr l n nh tế ạ ị ớ ấ
Câu VII.a (1,0 đi m) ểCho khai tri n ể
( )
0
n
nk n k k
n
k
a b C a b
−
=
+ =
. Quy c s h ng th i c a khai tri n là s h ng ngướ ố ạ ứ ủ ể ố ạ ứ
v i k = i-1.ớ
Hãy tìm các giá tr c a x bi t r ng s h ng th 6 trong khai tri n ị ủ ế ằ ố ạ ứ ể
8
11
31log 3 1
log 9 7 2
5
2
2 2
x
x� �
� �
� �
−
−− +
++
� �
� �
� �
� �
là 224.
B. Theo ch ng trình nâng caoươ
Câu VI.b (2,0 đi m)ể
1. Trong m t ph ng v i h tr c t a đ ặ ẳ ớ ệ ụ ọ ộ Oxy cho hình ch nh t ABCD có ph ng trình c nh AB và đ ngữ ậ ươ ạ ườ
chéo BD l n l t là ầ ượ
2 1 0x y− + =
và
7 14 0x y− + =
, đ ng th ng AC đi qua đi m ườ ẳ ể
( )
2;1M
. Tìm t a đ các đ nhọ ộ ỉ
c a hình ch nh t.ủ ữ ậ
2. Trong không gian v i h tr c t a đ ớ ệ ụ ọ ộ Oxyz cho ba đi m ể
( ) ( ) ( )
2;3;1 , 1;2;0 , 1;1; 2A B C− −
. Tìm t a đ tr cọ ộ ự
tâm H và tâm đ ng tròn ngo i ti p tam giác ABCườ ạ ế
Câu VII.a (1,0 đi m) ểGi i b t ph ng trình ả ấ ươ
( )
2 2
3log 2 9log 2x x x− > −
…………………….H t…………………….ế
Câu 1: 2.(1,0 đi m)ể
Ta có
2
' 3 3y x m= −
Đ hàm s có c c đ i, c c ti u thì ph ng trình ể ố ự ạ ự ể ươ
' 0y=
có hai nghi m phân bi t ệ ệ
0m
>�
Vì
1. ' 2 2
3
y x y mx= − +
nên đ ng th ng ườ ẳ
∆
đi qua c c đ i, c c ti u c a đ th hàm s có ph ng trình là ự ạ ự ể ủ ồ ị ố ươ
2 2y mx= − +
Ta có
( )
2
2 1
, 1
4 1
m
d I R
m
−
∆ = < =
+
(vì m > 0), ch ng t đ ng th ng ứ ỏ ườ ẳ
∆
luôn c t đ ng tròn tâm I(1; 1), bán kính R = 1 t i 2ắ ườ ạ
đi m A, B phân bi tể ệ
V i ớ
1
2
m
, đ ng th ng ườ ẳ
∆
không đi qua I, ta có:
2
1 1 1
. .sin
2 2 2
ABI
S IA IB AIB R
∆= =
Nên
IAB
S∆
đ t giá tr l n nh t b ng ½ khi sinAIB = 1 hay tam giác AIB vuông cân t i Iạ ị ớ ấ ằ ạ
1
2 2
R
IH = =�
(H là trung đi m c aể ủ
AB)
2
2 1 1 2 3
2
2
4 1
mm
m
−
= =� �
+
Câu 2:.(1,0 đi m)ể
Đ t ặ
( )
2 2 4 2
2 4 2 2t x x t x x= + = +�
ta đ c ph ng trìnhượ ươ
224
1 5 2 8 0 2
2
t
tt t t t
= −
+ = − + − =� � =
V i ớ
4t
= −
ta có
( )
00 0
2
2 4 4 2
4 2 4 2 2
2 2 16 2 8 0 2
xx x
x x x
x x x x x
<< <
+ = − = −���� + = + − = =
� �
� � �
� �
V i ớ
2t=
ta có
( )
2
4 2 4 2 2
00
0
2 4 2 3 1
224 2 2 0 3 1
xx
x
x x x
x x x x x
>
>
>
� �
+ = = −����
� � �
+ = + − = = −
Câu 3: (1,0 đi m)ể
∫∫ +
+
=
e
1
2
e
1
xdxlnx3dx
xln1x
xln
I
=I1+3I2
+) Tính
∫+
=
e
dx
xx
x
I
1
1ln1
ln
.
Đ t ặ
21
1 ln 1 ln ; 2t x t x tdt dx
x
= + = + =�
Khi
2tex;1t1x =⇒==⇒=
( ) ( )
( )
2
23
12 2 2
2 2 2
.2 2 1 2
13 3
1 1 1
tt
I tdt t dt t
t
−−
= = − = − =�� � � �
� �
� �
� �
+) TÝnh
dxxlnxI
e
1
2
2∫
=
. §Æt
=
=
⇒
=
=
3
x
v
x
dx
du
dxxdv
xlnu
32
+
= − = − = − + =�e
3 3 3 3 3 3
e 2 e
2 1 1
1
x 1 e 1 x e e 1 2e 1
I .lnx x dx .
3 3 3 3 3 3 9 9 9
=+= 21 I3II
3
e2225 3
+−
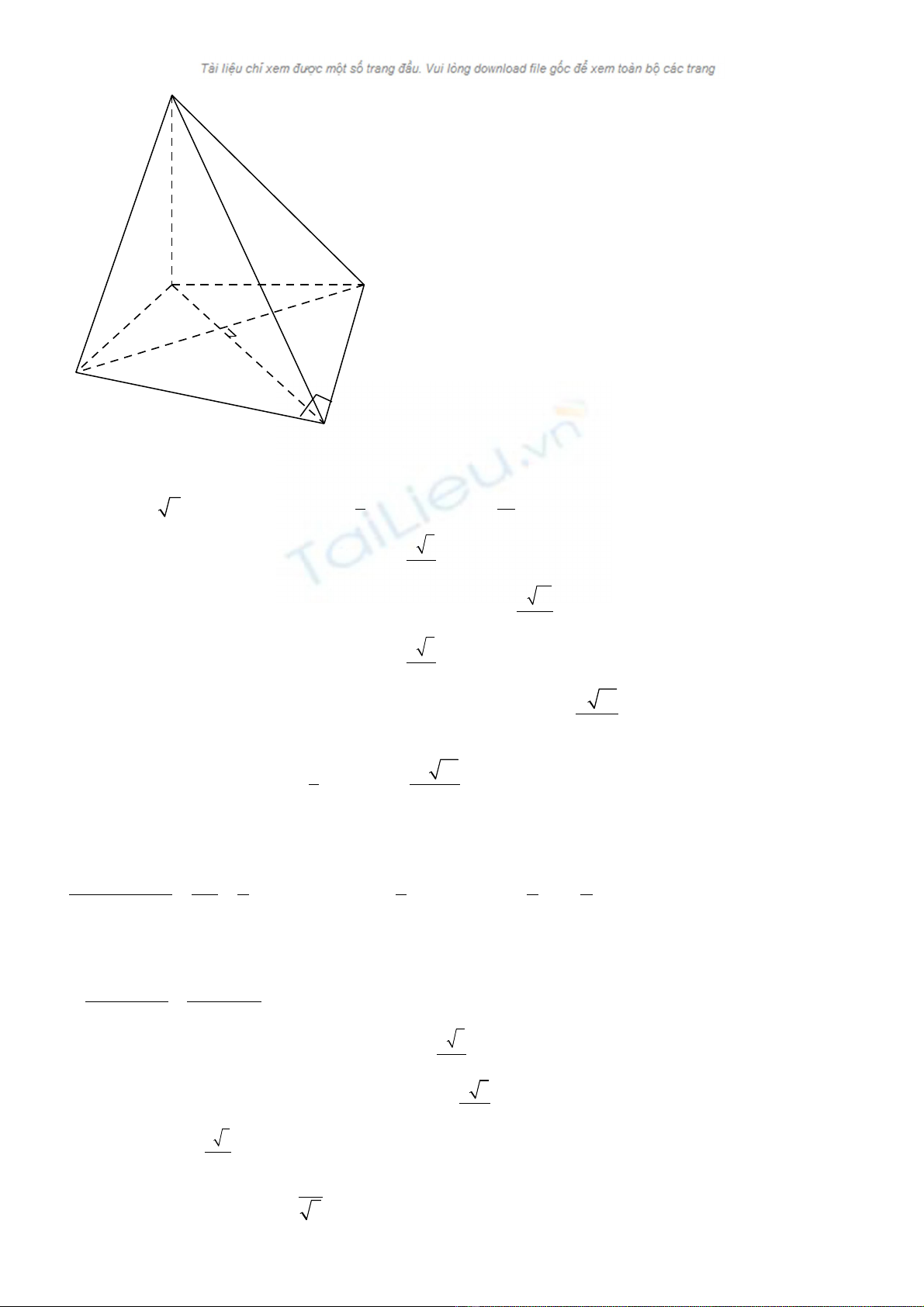
Câu : 4(1,0 đi m) *Ta có ể
2IA IH= −
uur uuur
H thu c tia đ i c a tia IAộ ố ủ
và
2IA IH=
2 2BC AB a= =
Suy ra
3
,2 2
a a
IA a IH AH IA IH= = = + =�
Ta có
5
2 2 2 0
2 . .cos 45 2
a
HC AC AH AC AH HC= + − =�
Vì
( ) ( )
( )
15
0 0
, 60 . tan 60 2
a
SH ABC SC ABC SCH SH HC⊥ = = = =� � �
Ta có
5
2 2 2 0
2 . .cos 45 2
a
HC AC AH AC AH HC= + − =�
Vì
( ) ( )
( )
0 0 15
, 60 .tan 60 2
a
SH ABC SC ABC SCH SH HC⊥ = = = =� � �
Th tích kh i chóp S.ABCD là: ể ố
( )
3
.
1 15
.
3 6
S ABC ABC
a
V S SH dvtt
∆
= =
*
( )
BI AH BI SAH
BI SH
⊥
⊥�
⊥
( )
( )
( )
( )
( )
( )
( )
( )
,1 1 1
, ,
2 2 2 2
,
d K SAH SK a
d K SAH d B SAH BI
SB
d B SAH = = = = =� �
Câu 5(1,0 đi m) Do a, b, c > 0 và ể
2 2 2 1abc+ + =
nên
( )
, , 0;1abc
Ta có
( )
2
2
5 3 1
23
2 2 2
1
a a
a a a a a
b c a
−
− + = = − +
+ −
B t đ ng th c tr thành ấ ẳ ứ ở
( ) ( ) ( )
2 3
3 3 3
3
a a b b c c− + + − + + − +
Xét hàm s ố
( ) ( )
( )
30;1f x x x x= − +
. Ta có:
( )
( )
0;1
2 3
ax 9
M f x =
( ) ( ) ( )
2 3
3
f a f b f c+ +� �
D u “=” x y ra khi và ch khi a = b = c=ấ ả ỉ
1
3
S
H
C
A
B
I
K
.