Đ THI TH Đ I H C, CAO Đ NG 2012Ề Ử Ạ Ọ Ẳ
Môn thi : TOÁN (Đ 145 )Ề
I. PH N CHUNG (7 đi m) (Cho t t c các thí sinh)Ầ ể ấ ả
Câu 1 (2đ) Cho hàm s : y = 2xố3 - 3x2 + 1 (1)
1. Kh o sát s bi n thiên và v đ th (C) c a hàm s (1)ả ự ế ẽ ồ ị ủ ố
2. Tìm trên (C) nh ng đi m M sao cho ti p tuy n c a (C) t i M c t tr c tung t i đi m có tungữ ể ế ế ủ ạ ắ ụ ạ ể
đ b ng 8.ộ ằ
Câu 2 (2đ) 1. Gi i h ph ng trình: ả ệ ươ
+=
−=−
2
2
3
1
9
1218
yxy
xxy
2. Gi i ph ng trình: 9ả ươ x + (
x
- 12).3x + 11 -
x
= 0
Câu 3 (1đ) Tính th tích kh i chóp tam giác đ u S.ABC có c nh đáy b ng a và kho ng cách gi aể ố ề ạ ằ ả ữ
c nh bên và c nh đáy đ i di n b ng m.ạ ạ ố ệ ằ
Câu 4 (1đ) Tính tích phân:
∫++−=
2
2
0
)]4ln()2([ dxxxxI
Câu 5 (1đ) Cho tam giác ABC, v i BC = a, CA = b, AB = c. ớ
Tho mãn h đi u ki n: ả ệ ề ệ
=+
=+
2
2
)(
)(
cabb
bcaa
CMR:
CBA sin
1
sin
1
sin
1+=
II. PH N RIÊNG (3đ) (Thí sinh ch làm m t trong hai ph n)Ầ ỉ ộ ầ
Theo ch ng trình chu n:ươ ẩ
Câu 6a (2đ)
1. Trong m t ph ng (oxy) cho đ ng th ng (d): 3x - 4y + 5 = 0 và đ ng tròn (C): xặ ẳ ườ ẳ ườ 2 + y2 + 2x
- 6y + 9 = 0
Tìm nh ng đi m M ữ ể
∈
(C) và N
∈
(d) sao cho MN có đ dài nh nh t.ộ ỏ ấ
2. Trong không gian (oxyz) cho hai m t ph ng:ặ ẳ
(P1): x - 2y + 2z - 3 = 0
(P2): 2x + y - 2z - 4 = 0 và đ ng th ng (d): ườ ẳ
3
4
21
2−
=
−
=
−
+zyx
L p ph ng trình m t c u (S) có tâm I ậ ươ ặ ầ
∈
(d) và ti p xúc v i hai m t ph ng (Pế ớ ặ ẳ 1), (P2).
Câu 7a (1đ) Đ t: (1 - x + xặ2 - x3)4 = a0 + a1x + a2x2 + ... + a12x12.
Tính h s aệ ố 7.
Theo ch ng trình nâng caoươ
Câu 6b (2đ)
1. Trong m t ph ng (oxy) cho đ ng tròn (C): (x + 1ặ ẳ ườ )2 + (y - 3)2 = 1 và đi m ể
M
5
7
,
5
1
. Tìm trên (C) nh ng đi m N sao cho MN có đ dài l n nh t.ữ ể ộ ớ ấ
2. Trong không gian (oxyz), cho m t c u (S): xặ ầ 2 + y2 + z2 + 2x - 4y - 2z + 5 = 0 và m t ph ngặ ẳ
(P): x - 2y + 2z - 3 = 0.
Tìm nh ng đi m M ữ ể
∈
(S), N
∈
(P) sao cho MN có đ dài nh nh t.ộ ỏ ấ
Câu 7b (1đ) Dùng đ nh nghĩa, tính đ o hàm c a hàm s :ị ạ ủ ố
x
xx
xf 2131
)(
3+−+
=
khi x
0, và
0)0( =f
; t i đi m xạ ể 0 = 0.
ĐÁP ÁN Đ THI TH Đ I H C, CAO Đ NG 2012Ề Ử Ạ Ọ Ẳ
Môn thi : TOÁN (Đ 145 )Ề
I. PH N CHUNG (7 đi m)Ầ ể ĐI MỂ
Câu 1 (2đ) y = 2x3 - 3x2 + 1
1) Kh o sát và v đ th (C)ả ẽ ồ ị
* TXĐ: R
* S bi n thiên:ự ế + Gi i h n: ớ ạ
−∞→x
ylim
=
∞−
,
−∞→x
ylim
=
∞+
0,25đ
+ B ng bi n thiên: y’ = 6xả ế 2 - 6x = 6x (x - 1)
y' = 0
==
==
⇔)0(;1
)1(;0
yx
yx
0,25đ
L p BBT; nêu đúng các kho ng đ n đi u và các đi m c c trậ ả ơ ệ ể ự ị 0,25đ
* Đ th : (t v ), rõ ràng, đ y đ , chính xác.ồ ị ự ẽ ầ ủ 0,25đ
2) Tìm M
∈
(C) ?
Gi s M (xả ử 0; y0)
∈
(C)
⇒
y0 = 2x03 - 3x02 + 1
Ti p tuy n (ế ế
) c a (C) t i M:ủ ạ
y = (6x02 - 6x0) (x - x0) + 2x03 - 3x02 + 1 0,25đ
(
) đi qua đi m P(0 ; 8) ể
⇔
8 = -4x03 + 3x02 + 1
⇔
(x0 + 1) (4x02 - 7x0 + 7) = 0 0,25đ
⇔
x0 = -1 ; (4x02 - 7x0 + 7 > 0,
∀
x0) 0,25đ
V y, có duy nh t đi m M (-1 ; -4) c n tìm.ậ ấ ể ầ 0,25đ
Câu 2 (2đ)
1) Gi i h :ả ệ
≥⇒≥⇒+=
≤⇒≥−⇒−=−
3232
3
1
9
320121218
2
22
xyyxyxy
xxxxy
0,25đ
1832 =⇒=⇒ xyx
0,25đ
{ }
32;32−∈⇒ x
, t ng ng y ươ ứ
{ }
33;33−∈
0,25đ
Th l i, tho mãn h đã choử ạ ả ệ
V y, ậ
( )
( ) ( ){ }
33;32,33;32; −−∈yx
0,25đ
2) Gi i ph ng trìnhả ươ :
( )
( )
0113123 2=−+−+ xx xx
−=
=
⇔x
x
x
113
13
=−+=
=
⇔(*)0113)(
0
xxf
x
x
(a + b + c = 0) 0,5đ
(*)
0)2(
,013ln3)(' ⇒
=
∀>+=
f
xxf x
có nghi m duy nh t ệ ấ
x
= 2 0,25đ
V y, t p nghi m c a ph ng trình: S = {0 ; 2}ậ ậ ệ ủ ươ 0,25đ
Câu 3 (1đ) S
N
A C
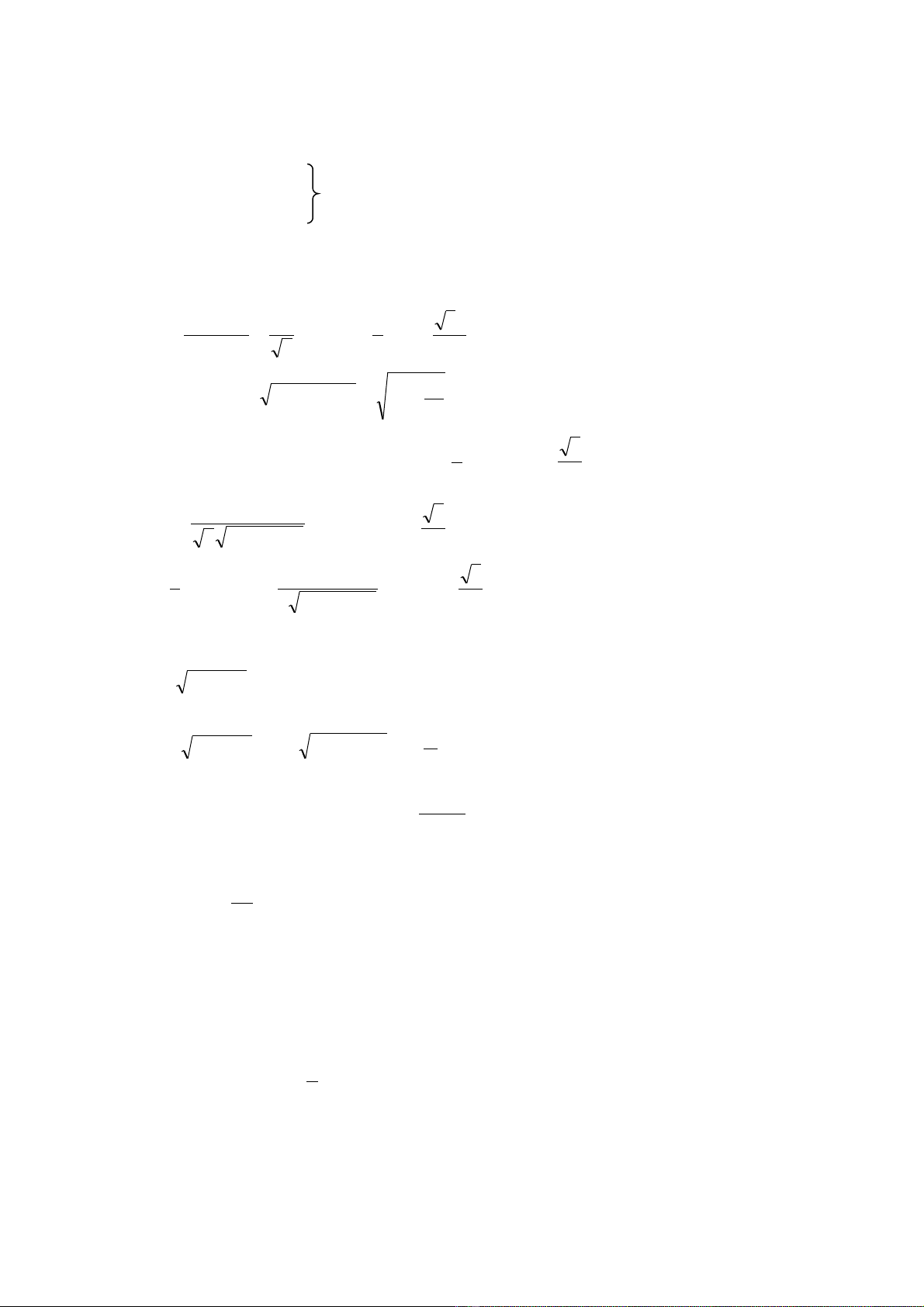
M
O
B
SO
⊥
(ABC)
S.ABC chóp
đ u ề
⇒
O là tâm tam giác đ u ABC.ề
MBCAO
=∩
⇒
)(SAMBC
BCSO
BCAM ⊥⇒
⊥
⊥
Trong
SAM k đ ng cao MN ẻ ườ
⇒
MN = m
2
3
2
3
3
60sin2 0
a
AOAM
aa
AO ==⇒==
0,25đ
3
SOSAhSO
2
222 a
hAO +=+=⇒=
SA.MN = SO.AM
( )
22222
3
4
43 mahma =−⇔
<am 2
3
0,25đ
22 433
2
ma
am
h−
=⇔
; và S(ABC) =
4
3
a20,25đ
22
3
436
).(
3
1
ma
ma
hABCSV −
==
<am 2
3
0,25đ
Câu 4 (1đ) Tính tích phân
∫−=
2
0
)2( dxxxI
+
∫+
2
0
2)4ln( dxx
=
21 II +
∫∫ =−−=−=
2
0
2
2
0
12
)1(1)2(
π
dxxdxxxI
(s d ng đ i bi n: ử ụ ổ ế
tx sin1
+=
) 0,25đ
∫∫ +
−+=+=
2
0
2
2
2
0
2
2
0
2
24
2|)4ln()4ln( dx
x
x
xxdxxI
(T ng ph n)ừ ầ 0,25đ
42ln6 −+=
π
(đ i bi n ổ ế
tx tan2=
) 0,25đ
2ln64
2
3
21 +−=+=
π
III
0,25đ
Câu 5 (1đ)
ABC:
=+
=+
)2()(
)1()(
2
2
cabb
bcaa
(1)
⇒
sin2A + sinAsinC = sin2B (Đl sin)
⇒
sinAsinC =
2
1
(cos2A - cos2B)
⇒
sinAsinC = sin(A + B) sin (B -A)
⇒
sinA = sin (B - A) ; (sin (A + B) = sin C > 0)
⇒
A = B - A ; (A, B là góc c a tam giác)ủ
⇒
B = 2A 0,25đ
T ng t : (2) ươ ự
⇒
C = 2B
A + B + C =
, nên A =
7
π
; B =
7
2
π
; C =
7
4
π
0,25đ
Ta có:
CB sin
1
sin
1+
=
7
3
sin
7
cos
7
sin2
7
cos
7
3
sin2
7
4
sin
7
2
sin
7
2
sin
7
4
sin
πππ
ππ
ππ
ππ
=
+
0,25đ
=
Asin
1
7
sin
1=
π
(đpcm) 0,25đ
II. PH N RIÊNG (3 đi m)Ầ ể
Ch ng trình c b nươ ơ ả
Câu 6a (2đ)
1) Tìm M
∈
(C), N
∈
(d)?
(d): 3x - 4y + 5 = 0
(C): (x + 1)2 + (y - 3)2 = 1
⇒
Tâm I (-1 ; 3), bán kính R = 1
d (I ; d) = 2
⇒
(d)
∩
(C) = Ø
Gi s tìm đ c Nả ử ượ 0
∈
(d)
⇒
N0 là hình chi u vuông góc c a I trên (d)ế ủ
⇒
N0 = (d)
( )
∆∩
, v i: ớ
( )
( ) ( )
−=⇒⊥∆
−∋∆
∆
4;3)(
)3;1(
ud
I
0,25đ
( )
⇒
−=
+−=
∆⇒ 5
7
;
5
1
43
31
:0
N
ty
tx
0,25đ
Rõ ràng
( )
∩∆
(C) = {M1; M2} ; M1
−5
11
;
5
2
; M2
−5
19
;
5
8
M0
∈
(C) đ Mể0N0 nh nh t ỏ ấ
⇒
M0
≡
M1 và M0N0 = 1 0,25đ
K t lu n: Nh ng đi m c n tìm tho mãn đi u ki n bài toán.ế ậ ữ ể ầ ả ề ệ
M
−5
11
;
5
2
; N
5
7
;
5
1
0,25đ
2) Ph ng trình m t c u (S) ?ươ ặ ầ
(P1): x - 2y + 2z - 3 = 0
(P2): 2x + y - 2z - 4 = 0
Gi s I (xả ử 0 ; y0 ; z0)
∈
(d):
3
4
21
2−
=
−
=
−
+zyx
⇒
I (-2 - t ; 2t ; 4 + 3t) là tâm c a m t c u (S)ủ ặ ầ 0,25đ
M t c u (S) ti p xúc v i (Pặ ầ ế ớ 1), (P2)
⇔
d (I, (P1)) = d (I ; (P2))
⇔
−=
−=
⇔+=+ 1
13
1610
3
1
39
3
1
t
t
tt
0,25đ
⇒
I1 = (11 ; 26 ; -35) ; I2 (-1 ; 2 ; 1)
⇒
R1 = 38 ; R2 = 2 0,25đ
V y, có hai m t c u c n tìm:ậ ặ ầ ầ
(S1): (x - 11)2 + (y - 26)2 + (z + 35)2 = 382
(S2): (x + 1)2 + (y - 2)2 + (z - 1)2 = 220,25đ
Câu 7a (1đ) Tính h s aệ ố 7 ?
(1 - x + x2 - x3)4 = (1 - x)4 (1 + x2)4 0,25đ
=
( )
−∑∑ ==
4
0
2
4
4
0
4
1
i
ii
k
kk
kxCxC
0,25đ
(Gt)
{ } ( ) ( ) ( ){ }
2;3,3;1;
4,3,2,1,0,
72 ∈⇒
∈
=+
⇒ik
ik
ik
0,25đ
40
2
4
3
4
3
4
1
47 −=−−=⇒ CCCCa
0,25đ
Ch ng trình nâng caoươ
Câu 6b (2đ)
1) Tìm N
∈
(C)?
(C): (x + 1)2 + (y - 3)2 = 1
⇒
Tâm I (-1 ; 3), bán kính R = 1 ; M
5
7
;
5
1
2
5
8
;
5
6=⇒
−= MIIM
0,25đ
Gi s tìm đ c N ả ử ượ
∈
(C)
⇒
MN
≤
MI + IN = 3 0,25đ
D u “=” x y ra ấ ả
⇔
N là giao đi m c a tia đ i IM và đ ng tròn (C).ể ủ ố ườ
(IM):
−=
+−=
ty
tx
5
8
3
5
6
1
;
( ) ( ) { }
21;NNCIM =∩
−⇒ 5
11
;
5
2
1
N
,
−5
19
;
5
8
2
N
; MN1 < MN20,25đ
K t lu n: Tho mãn đi u ki n bài toán: ế ậ ả ề ệ
−5
19
;
5
8
N
0,25đ
2) Tìm M
∈
(S) , N
∈
(P) ?
(S): (x + 1)2 + (y - 2)2 + (z - 1)2 = 1
Tâm I (-1 ; 2 ; 1), bán kính R = 1
(P): x - 2y + 2z - 3 = 0
⇒
d
( )( )
PI;
= 2
Ø)()( =∩⇒ SP
Gi s tìm đ c Nả ử ượ 0
∈
(P)
⇒
N0 là hình chi u vuông góc c a I trên (P)ế ủ 0,25đ
( ) ( )
PdN ∩=⇒ 0
, v i: ớ
( )
−=⇒⊥
−∋
)2;2;1()()(
)1;2;1(
d
uPd
Id
( )
+=
−=
+−=
⇒
tz
ty
tx
d
21
22
1
:
−⇒ 3
7
;
3
2
;
3
1
0
N
0,25đ
=∩ )()( Sd
{M1 ; M2}