SỞGD ĐTQUẢNGNINH KÌTHITHỬĐẠIHỌCNĂMHỌC20102011
TRƯỜNGTHPTTRẦNNHÂNTÔNG
MÔNTOÁN
(Thờigianlàmbài: 180phút)
A.PHẦNDÀNHCHOTẤTCẢTHÍSINH
CâuI(2điểm)Chohàmsố 34 24 + - = xxy(C)
1.Khảosátsựbiếnthiênvàvẽđồthị (C)
2.Tìmmđểphươngtrình:mxx2
22 log3)1( = - -có2nghiệmphânbiệt.
CâuII(2điểm)a)Giảiphươngtrình:xxxx 2sin21cos3sintan 222 + = -
b)Giải hệ phươngtrình: ï
î
ï
í
ì
+ = -
= + + -
xxyyyx
yyxyyx
3
41
22
2222
CâuIII(1điểm) Tínhtíchphân ò + + +
=
4
0 )
4
sin(22sin1
2cos
p
p
dx
xx
x
I
CâuIV(1điểm)ChohìnhchópSABCDcóđáyABCDlàhìnhvuôngcạnha,tamgiácSABđều,tamgiácSCDvuôngcân
tạiS.GọiI,J,KlầnlượtlàtrungđiểmcủacáccạnhAB,CD,SA.Chứngminhrằng )()( ABCDSIJ ^.Tínhthểtíchkhối
chópK.IBCD.
CâuV(1điểm):
a,(ThísinhthikhốiB,Dkhônglàmcâunày)Chocácsố thựcdươngcba ,, thỏamãn: 1
222 = + + cabcab.
Tìmgiátrịnhỏnhấtcủaac
c
cb
b
ba
a
P222
444
+
+
+
+
+
=
b(ThísinhthikhốiAkhônglàmcâunày).Tìmmđểphươngtrìnhsaucónghiệm:
mxmxmxx 4)2(2)2(8 24 + + - - = +
B.PHẦNDÀNHCHOTỪNGLOẠITHÍSINH
Phầndànhchothísinhthitheochươngtrìnhchuẩn
CâuVIa(2điểm)
1.Trongmặtphẳngtoạđộ Oxy,chotamgiácABCcótrungđiểmcạnh BClàM(3;2),trọngtâmvàtâmđườngtrònngoaitiếp
tamgiácABClầnlượtlàG( 3
2
;
3
2 ),I(1;2).Xácđịnhtọađộ đỉnhC.
.2.TrongkhônggiantọađộOxyzchohaiđườngthẳng 2
2
3
2
1
1
:;
1
2
12
1
: 21 -
-
=
+
=
-
-
+
= =
- zyx
d
zyx
d
Chứngminhrằng 1
dvà 2
dchéonhau.Lậpphươngtrình đườngthẳng Dsongsongvớimặtphẳng(P)
07 = - + + zyxcắt 1
d, 2
dtại2điểmsaochokhoảngcách2điểmđólàngắnnhất.
CâuVIIa(1điểm)Gọi 321 ,, zzzlàcácnghiệmcủaphươngtrình: 02
23 = + - zz,Cz Î.Tínhizzz 2
2
3
2
2
2
1 - + +
Phầndànhchothísinhthitheochươngtrìnhnângcao
CâuVIb(2điểm)
1. Trongmặtphẳngtoạđộ Oxy ,chohìnhthoiABCDbiếtđườngthẳngACcóphươngtrình : 03 = + -yx;đỉnhB(4;1).
ĐiểmM(0;1)nằmtrêncạnhAB.Xácđịnhtọađộ cácđỉnhcònlaicủahìnhthoi.
2. TrongkhônggiantọađộOxyzchohaiđườngthẳng 2
2
3
2
1
1
:;
1
2
12
1
: 21 -
-
=
+
=
-
-
+
= =
- zyx
d
zyx
d
Chứngminhrằng 1
dvà 2
dchéonhau.Viếtphươngtrìnhmặtphẳng songsongvớimặtphẳng(P) 07 = - + + zyxcắt
1
d, 2
dtại2điểmphânbiệtsaochokhoảng cáchgiữahaiđiểmđóngắnnhất.
CâuVIIb(1điểm)Giảibấtphươngtrình: 253..22.4253 222 + - - > + - + - - xxexxexxx xx
……...HẾT...........
Cánbộcoithikhônggiảithíchgìthêm!
thienthan9x@gamil.comsentto www.laisac.page.tl
ĐỀCHÍNHTHỨC
ĐÁPÁNHƯỚNGDẪNCHẤMMÔNTOÁN
CâuIChohàmsố 34 24 + - = xxy(C)
1.Khảosátsựbiếnthiênvàvẽđồthị (C )
2.Tìmmđểphươngtrình:mxx2
22 log3)1( = - -có2nghiệmphânbiệt.điểm
1
H
ọcsinhtựlàm
1 điểm
Sốnghiệmcủaphươngtrìnhchínhlàsốgiaođiểmcủađồthịhàmsố 3)1( 22 - - = xxy
(C’)vàđườngthẳngmy2
log = .0,25
Tacó:
ï
î
ï
í
ì
< < - + - -
+¥ È - -¥ Î + -
= - - =
33)34(
);3[]3;(34
3)1(
24
24
22
xkhixx
xkhixx
xxy
Từđótacó:Với );3[]3;( +¥ È - -¥ Îxthì (C’)º(C)
Với 33 < < - xthì (C’)đốixứngvới (C)quaOy
0,25
0,25
2
Từđồthịtacó:Phươngtrìnhcó 2nghiệmphânbiệt Û ê
ê
ë
é
< <
>
Û
ê
ë
é
< < -
>
1
8
1
2
0log3
1log
2
2
m
m
m
m0,25
CâuII
a)
Giảiphươngtrình:xxxx 2sin21cos3sintan 222 + = -1điểm
Điềukiện: Z Î + ¹ Û ¹ nnxx ,
2
0cos
p
p
0,25
Chiacảhaivếchox
2
cos tađược:
xxx tan4tan13tan 24 + + = - ê
ê
ë
é
- - =
+ =
Û + = Û2tantan
2tantan
)2(tantan 2
2
24
xx
xx
xx
0,25
Với 2tantan
2 + = xx ê
ë
é
=
- =
Û = - - Û2tan
1tan
02tantan
2
x
x
xx0,25
y
x
my2
log =
-3
1
3 -3
Zk
kx
kx Î
ê
ê
ë
é
+ =
+
-
=
Û ,
2arctan
4
p
p
p
Với 02tantan2tantan 22 = + + Û - - = xxxx(vônghiệm)
VậyphươngtrìnhcónghiệmZk
kx
kx Î
ê
ê
ë
é
+ =
+
-
=,
2arctan
4
p
p
p
0,25
Giảihệphươngtrình: ï
î
ï
í
ì
+ = -
= + + -
xxyyyx
yyxyyx
3
41
22
22221điểm
+Nhậnxét:Nếu 0 =xtacó ï
î
ï
í
ì
= -
= +
0
81
2
2
y
yyvôlý,nếu 0 =ytacó î
í
ì
=
=
0
01
xvôlý
Từđótacóhệcónghiệmthì 0;0 ¹ ¹ yx
0,25
+Tacóhệtươngđương
ï
ï
î
ï
ï
í
ì
= - -
= + - +
3
1
4
11
2
2
yx
y
x
y
y
xx
ï
ï
î
ï
ï
í
ì
= - -
= - + +
Û
3)
1
(
4)
1
()
1
( 2
2
x
y
y
x
y
x
y
x0,25
Đặt
ï
ï
î
ï
ï
í
ì
=
- =
x
y
v
y
xu1
Hệtrởthành: ï
î
ï
í
ì
= -
= + +
3
4
2
2
vu
u
v
u
î
í
ì
- =
± = =
Û3
7;2
uv
uu0,25
b)
Thaylạihệtađượccácnghiệm: )
2
738100737
;
)73(2
738100737
();1;1( + +
+
+ ± - -
- m0,25
Tínhtíchphân ò + + +
=
4
0 )
4
sin(22sin1
2cos
p
p
dx
xx
x
I
1điểm
Tacó ò + + +
-
=
4
0
2
22
)cos(sin2)cos(sin
sincos
p
dx
xxxx
xx
I
0,25
Theocôngthứctíchphântừngphầntacó:
ò + + +
+ -
=
4
0 )2cos)(sincos(sin
)sin)(cossin(cos
p
dx
xxxx
xxxx
I= ò + +
-
4
0 2cossin
)sin(cos
p
dx
xx
xx
0,25
4
0
4
0
)2cosln(sin
2cossin
)2cos(sin
p
p
+ + =
+ +
+ +
= òxx
xx
xxd
0,25
CâuIII
Thayvàotađược: )224ln(
12
22
ln - =
+
=I0,25
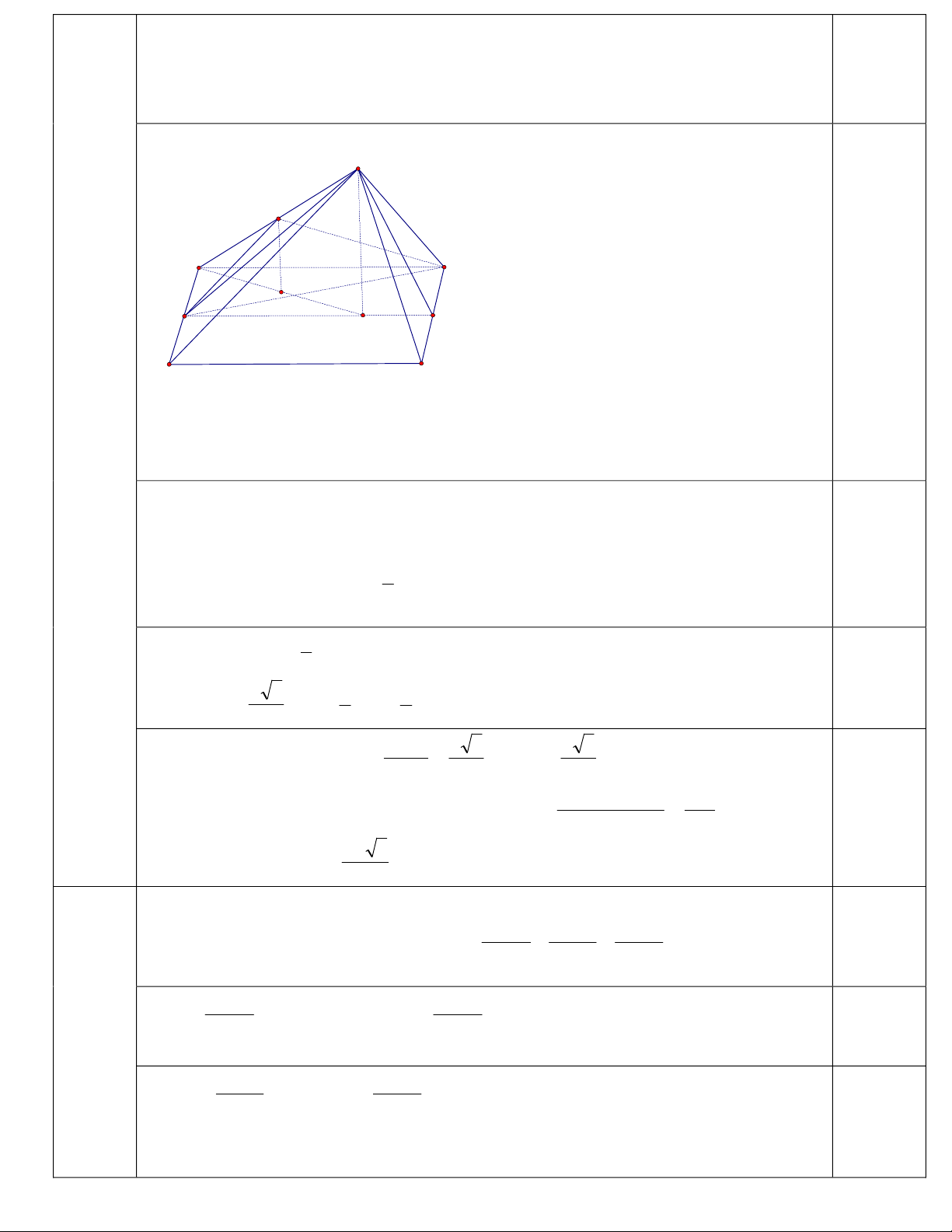
ChohìnhchópSABCDcóđáyABCDlàhìnhvuôngcạnha,tamgiácSABđều,tamgiácSCD
vuông cân tại S.Gọi I,J,K lần lượt là trung điểm của các cạnh AB,CD,SA .Chứng minh rằng
)()( ABCDSIJ ^.TínhthểtíchkhốichópK.IBCD.
K '
K
J
I
A
B C
D
S
H
Từgiảthiếttacó:
)(SIJAB
IJAB
SIAB ^ Þ
þ
ý
ü
^
^Do )()()( ABCDSIJABCDAB ^ Þ Ì.
0,25
+KẻIJSH ^do )(
)()(
)()(ABCDSH
IJABCDSIJ
ABCDSIJ ^ Þ
þ
ý
ü
= Ç
^
+Goi K’làhìnhchiếuvuônggóccủaK lên (ABCD)khiđóSHKK //' do Klàtrungđiểm SA
nên K’làtrungđiểm AH&SHKK2
1
'=.
0,25
Từđótacó:IBCDIBCDK SKKV à
= '.
3
1
.
Dễthấy: 2
3a
SI =; 22
1 a
CDSJ = =;aIJ = SIJ D ÞvuôngtạiSvì: 222IJSJSI = +0.25
CâuIV
TừhệthứcSI.SJ=SH.IJ4
3. a
IJ
SJSI
SH = = Þ8
3
'a
KK = Þ
TacóIBCD àlàhìnhthangvuôngtaiBvàCnên 4
3
2
).( 2
aBCCDIB
S IBCD =
+
=
à
Thayvàotađược 32
3.
3
.
a
V IBCDK =
0.25
Chocácsốthựcdươngcba ,, thỏamãn: 1
222 = + + cabcab.
Tìmgiátrịnhỏnhấtcủaac
c
cb
b
ba
a
P222
444
+
+
+
+
+
=
1điểm
+Tacó: 32
4
6)2(
2
9aaba
ba
a ³ + +
+ Ûbaa
ba
a23
4
25
2
9 - ³
+ ;0,25
CâuV
Tươngtựcbb
cb
b23
4
25
2
9 - ³
+ ;acc
ac
c23
4
25
2
9 - ³
+
³ Þ P9 )(2)(5 222333accbbacba + + - + +
0,25
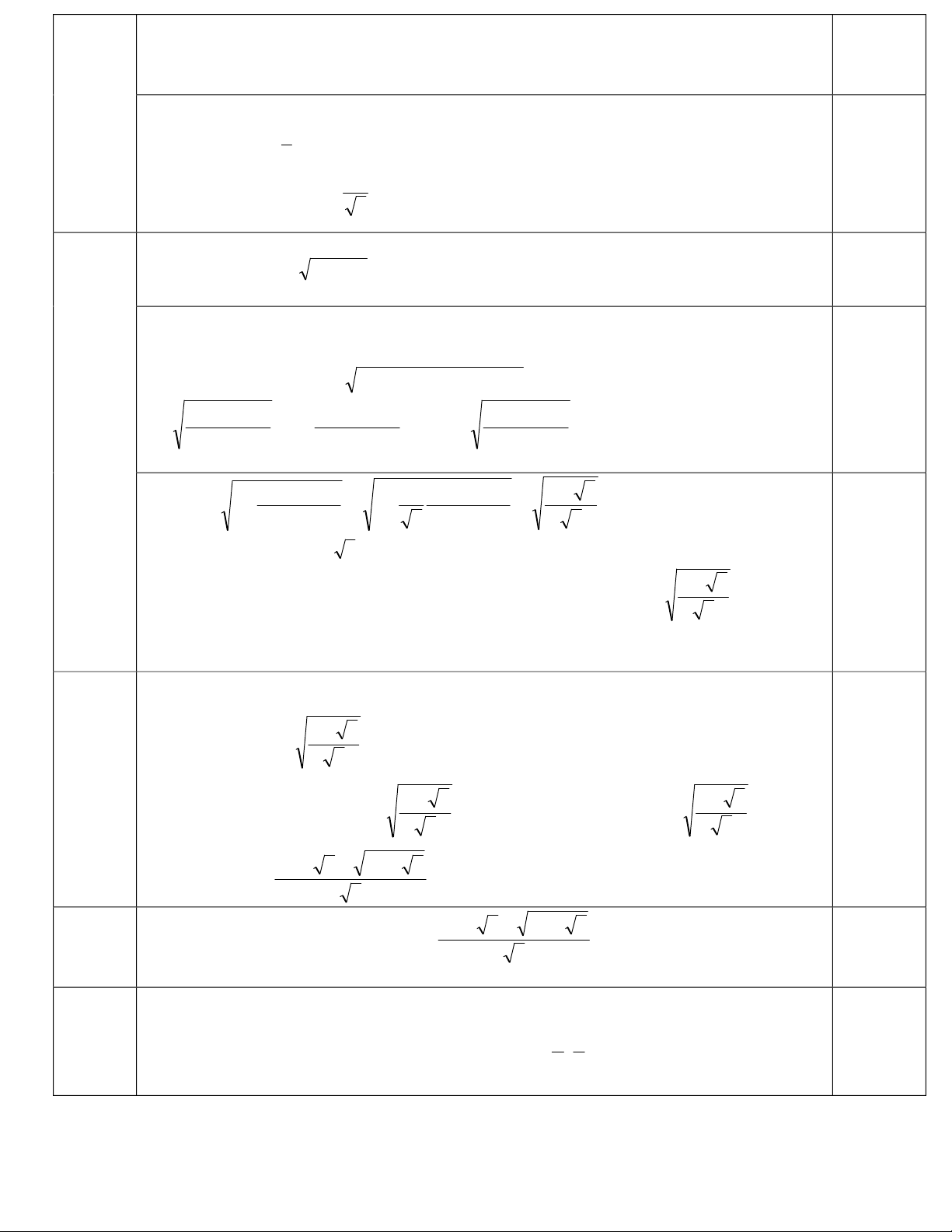
+Tacó:acacccbcbbbabaa233323332333 3;3;3 ³ + + ³ + + ³ + +
Þaccbbacba222333 + + ³ + + ³ Þ P9 )(3 333cba + +
0,25
Tươngtựtacũngcó : 1
222333 = + + ³ + + cabcabcba
3
1
39 ³ Û ³ Þ PP
Dấu“=”xảyra 3 3
1
= = = cba0.25
Tìmmđểphươngtrìnhsaucónghiệm:
mxmxmxx 4)2(2)2(8 24 + + - - = +
Điềukiện: ê
ë
é
- £
³
2
0
x
x
Phươngtrìnhtrươngđương: )42(42)42)(2( 2222 + - + - - = + - + xxmxxxxxx(1)
m
xx
xx
xx
xx +
+ -
+
- =
+ -
+
Û42
2
2
42
2
2
2
2
2
Đặt 0
42
2
2
2 ³ =
+ -
+t
xx
xx
0.25
Tacó: 3
32
3)1(
3)1(
3
2
1
3)1(
)1(4
1 2
2
2
+
=
+ -
+ -
+ £
+ -
-
+ =x
x
x
x
t .
Dấu“=”xẩyra 31+ = Ûx .
Do )(xtlàhàmsốliêntuctrêncáckhoảng ]2;( - -¥và );0[ +¥nên ú
ú
û
ù
ê
ê
ë
é +
Î3
32
;0t (cóthểlập
bảngbiếnthiênđểchỉrađiềunày)
0.25
Phươngtrìnhtrởthànhmtt = +
2
2 (2).Phương trình(1)cónghiệmkhivàchỉkhiphươngtrình
(2)cónghiệm ú
ú
û
ù
ê
ê
ë
é +
Î3
32
;0t
Xét ú
ú
û
ù
ê
ê
ë
é +
Î " + =3
32
;0,2)( 2ttttfcó 014)(' > + = ttf ú
ú
û
ù
ê
ê
ë
é +
Î "3
32
;0t
Dođó 3
323324
)(0 + + +
£ £ tf
0.25
Vậyphươngtrìnhcónghiệmkhi 3
323324
0 + + +
£ £m
0.25
CâuVIa
1Trongmặtphẳngtoạđộ Oxy,chotamgiácABCcótrungđiểmcạnhBClàM(3;2),trọngtâmvà
tâmđườngtrònngoaitiếptamgiácABClầnlượtlàG( 3
2
;
3
2 ),I(1;2).Xácđịnhtọađộ đỉnhC.
1điểm
![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)
![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)
