
TR NG THPT LONG MƯỜ ỸĐ THI TH Đ I H C NĂM H C 2012-2013Ề Ử Ạ Ọ Ọ
GV RA Đ BÙI VĂN NH NỀ Ạ Môn thi TOÁN: Giáo d c trung h c ph thôngụ ọ ổ
Ngày 3 tháng 2 năm 2013
(Đ chính th c có 01 trang) ề ứ Th i gian: 180 phút không k th i gian giao đờ ể ờ ề
I. PH N CHUNG CHO T T C THÍ SINH Ầ Ấ Ả (7,0 đi mể)
Câu I (2,0 đi mể) Cho hàm s ố
( ) ( )
3 2
3 1 1 1y x x m x= − + + +
có đ th ồ ị
( )
m
C
v i m là tham s ớ ố
1) Kh o sát s bi n thiên và v đ th (C) c a hàm s (1) khi ả ự ế ẽ ồ ị ủ ố
1m
= −
2) Tìm m đ đ ng th ng ể ườ ẳ
( )
: 1d y x= +
c t đ th ắ ồ ị
( )
m
C
t i 3 đi m phân bi t ạ ể ệ
( )
0,1 , ,P M N
sao cho bán
kính
đ ng tròn ngo i ti p tam giác ườ ạ ế
OMN
b ng ằ
5 2
2
v i ớ
( )
0;0O
Câu II (2,0 đi mể) 1) Gi i ph ng trình: ả ươ
2
2cos 2 2cos 2 4sin 6 cos 4 1 4 3 sin 3 cosx x x x x x− + + = +
2) Gi i b t ph ng trình: ả ấ ươ
5 4 10
2 2
x
x x x x
x
−
+ + −
Câu III (1,0 đi mể) Tính tích phân sau
4
3 4
0
1 sin 2
2sin cos cos
x
I dx
x x x
π
+
=+
Câu IV (1,0 đi mể) Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông t i A, ạ
2 2 .AC BC a= =
M t ặ
ph ng ẳ
( )
SAC
t o v i m t ph ng ạ ớ ặ ẳ
( )
ABC
m t góc ộ
0
60
. Hình chi u c a S lên m t ph ng ế ủ ặ ẳ
( )
ABC
là trung
đi m ể
H c a c nh BC. Tính th tích kh i chóp ủ ạ ể ố
.S ABC
và kho ng cách gi a hai đ ng th ng ả ữ ườ ẳ
AH
và
SB
.
Câu V (1,0 đi mể) Gi i ph ng trình ả ươ
( ) ( )
53 1
2
2
2 1 2 22 1 2 2
1 2 1 2
xx
x x x
x x
+
++ = + +
+ +
II. PH N T CH N (Ầ Ự Ọ 3,0 đi mể) - Thí sinh ch đ c làm m t trong hai ph nỉ ượ ộ ầ (ph n A ho c ph n Bầ ặ ầ )
A. Theo ch ng trình Chu nươ ẩ
Câu VI.a (2,0 đi mể) 1) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy cho đ ng tròn ườ
( ) ( ) ( )
2 2
: 3 1 9C x y− + − =
và
đ ng th ng ườ ẳ
( )
:d
10 0x y+ − =
. T đi m M trên ừ ể
( )
d
k hai ti p tuy n đ n ẻ ế ế ế
( )
C
, g i ọ
,A B
là hai ti pế
đi m.ể
Tìm t a đ đi m ọ ộ ể
M
sao cho đ dài đo n ộ ạ
3 2AB =
2) Trong không gian v i h t a đ ớ ệ ọ ộ
Oxyz
cho hai đi m ể
( ) ( )
1;1;2 , 0; 1;3A B −
. G i ọ
C
là giao đi m c a đ ngể ủ ườ
th ng ẳ
( )
AB
và
( )
mp Oxy
. Tìm t a đ đi m ọ ộ ể
M
trên đ ng th ng ườ ẳ
( )
AB
sao cho m t c u tâm ặ ầ
M
bán kính
MC
c t ắ
( )
mp Oxy
theo giao tuy n là đ ng tròn có bán kính b ng ế ườ ằ
2 5
.
Câu VII.a (1,0 đi mể) V i m i ớ ọ
, 3.n N nγ
Gi i ph ng trình ả ươ
3 3 3 3
3 4 5
1 1 1 1 89
..... 30
n
C C C C
+ + + + =
B. Theo ch ng trình Nâng caoươ
Câu VI.b (2,0đi mể) 1) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy cho tam giác
ABC
vuông t i ạ
A
, bi t ế
B
và
C
đ i x ng nhau qua g c t a đ O. Đ ng phân giác trong góc B c a tam giác ABC là đ ng th ng ố ứ ố ọ ộ ườ ủ ườ ẳ
( )
: 2 5 0d x y+ − =
. Tìm t a đ các đ nh c a tam giácọ ộ ỉ ủ
ABC
, bi t đ ng th ng ế ườ ẳ
AC
đi qua đi m ể
( )
6;2K
2) Trong không gian v i h t a đ ớ ệ ọ ộ
Oxyz
cho b n đi m ố ể
( ) ( ) ( ) ( )
0;0; 1 , 1;2;1 , 2;1; 1 , 3;3 3A B C D− − −
.. Tìm
t a đ đi m M thu c đ ng th ng ọ ộ ể ộ ườ ẳ
AB
và đi m N thu c tr c hoành sao cho đ ng th ng ể ộ ụ ườ ẳ
MN
vuông góc
v i đ ng th ng ớ ườ ẳ
CD
và đ dài ộ
3MN
=
Câu VII.b (1,0 đi mể) Tìm s nguyên d ng n th aố ươ ỏ
( )
0 1 2 3
1 1 1 1
1 1023
2 3 4 1
n
n n n n n
n C C C C C
n
� �
+ + + + + + =
� �
+
� �
L
TR NG THPT LONG M ĐÁP ÁN Đ THI TH Đ I H C NĂM H C 2012-2013ƯỜ Ỹ Ề Ử Ạ Ọ Ọ
GV RA Đ BÙI VĂN NH NỀ Ạ Môn thi TOÁN: Giáo d c trung h c ph thôngụ ọ ổ
ĐÁP ÁN – THANG ĐI M ỂĐ THI TH Đ I H C 03-02-2013Ề Ử Ạ Ọ
Câu Đáp án Điể
m
I
Cho hàm s ố
( ) ( )
3 2
3 1 1 1y x x m x= − + + +
có đ th ồ ị
( )
m
C
v i m là tham s ớ ố
1) Kh o sát s bi n thiên và v đ th (C) c a hàm s (1) khi ả ự ế ẽ ồ ị ủ ố
1m
= −
2) Tìm m đ đ ng th ng ể ườ ẳ
( )
: 1d y x= +
c t đ th ắ ồ ị
( )
m
C
t i 3 đi m phân bi tạ ể ệ
( )
0,1 , ,P M N
sao cho bán kính đ ng tròn ngo i ti p tam giác ườ ạ ế
OMN
b ng ằ
5 2
2
v i ớ
( )
0;0O
2,0
1) H c sinh t v ọ ự ẽ
2) Ph ng trình hoành đ giao đi m c a ươ ộ ể ủ
( )
m
C
và (d):
( )
3 2
3 1 1 1x x m x x− + + + = +
( )
( )
( )
2
2
0 1 0;1
3 0 3 0 2
x y P
x x x m x x m
= =� �
− + =� � − + =
Đ ể
( )
m
C
c t (d) t i 3 đi m phân bi t ắ ạ ể ệ
( )
2
có 2 nghi m phân bi t khác 0ệ ệ
0
9
4
m
m
<
Gi s ả ử
( ) ( )
1 1 2 2
; 1 , ; 1M x x N x x+ +
khi đó
1 2
;x x
là nghi m c a pt(2)ệ ủ
Ta có
( )
( )
1 . .
. ;
2 4
OMN
OM ON MN
S MN d O d R
= =
(v i R là ớbán kính đ ng trònườ
ngo i ti p tam giác ạ ế
OMN
)
( )
( )
( )
( )
( )
( )
( )
1 . .
. ; . 2 . ; 5 2 ; 3
2 4
OM ON
d O d OM ON R d O d d O d
R
= = =� �
Mà ta có
( ) ( )
2 2
1 1 1 1
. 2 2 1 2 2 1OM ON x x x x= + + + +
V i ớ
2 2
1 1 2 2
3 ; 3x x m x x m= − = −
2
. 4 12 25OM ON m m= + +�
( )
( )
1 2
* ; 2
2
d O d = =
Khi đó th vào (3) ta đ c ế ượ
20
2
4 12 25 5 2 5 3
2
m
m m m
=
+ + = = = −
th a đ chỏ ề ỉ
có
3m
= −
II
1) Gi i ph ng trình: ả ươ
2
2cos 2 2cos 2 4sin 6 1 cos 4 4 3 sin 3 cosx x x x x x− + = − +
1,0
2 2
2cos 2 2cos 2 4sin 6 2sin 2 4 3 sin 3 cospt x x x x x x− + = +�
2 2
cos 2 cos 2 2sin 6 sin 2 2 3 sin 3 cosx x x x x x− + = +�
2 2
cos 2 sin 2 cos 2 2sin 6 2 3 sin 3 cosx x x x x x− − + =�
cos 4 cos 2 2sin 6 2 3 sin 3 cosx x x x x− + =�
2sin 3 sin 4sin 3 cos3 2 3 sin 3 cosx x x x x x− + =�
( )
2sin 3 sin 2cos3 3 cos 0x x x x− − + =�
sin 3 0
sin 3 cos 2cos3
x
x x x
=
+ =
( )
* sin 3 0 3
x x k k Z
π
= =� �
*sin 3 cos 2cos3 cos cos3
6
x x x x x
π
� �
+ = − =�� �
� �
( )
12
24 2
x k
k Z
k
x
π
= − + π
� �
π π
= +
V y nghi m c a ph ng trình là ậ ệ ủ ươ
( )
; ;
12 24 2 3
k k
x k x x k Z
π π π π
= − + π = + =
2) Gi i b t ph ng trình: ả ấ ươ
( )
5 4 10
2 2 1
x
x x x x
x
−
+ + −
1,0
ĐK:
2
000
10 2 0 2 10 0
xxx
xx x
x
>
>
� � >� �
� �
+ − − +
Bpt(1)
( )
2 2 2 2
2 4 5 2 10 2 2 10 15 2 10x x x x x x x x− + − + − + − − +� � � �
Đ t ặ
( ) ( )
2
22 10 1 9 3 *t x x x= − + = − +
Bpt tr thành ở
( )
( )
2
5
2 15 0 3 *
2
3
t
t t t do
t
−
−−��
( ) ( )
2
2 2
3 2 10 3 2 1 0 1 0 /t x x x x x h n− + − + −� � � � � � �
V y nghi m b t ph ng trình là ậ ệ ấ ươ
( )
0;x+� �
III
Tính tích phân sau
4
3 4
0
1 sin 2
2sin cos cos
x
I dx
x x x
π
+
=+
1,0
( )
( )
( )
( )
( )
( ) ( )
( ) ( )
2 2
2
4 4
4
2 2
0 0
2 2
4 4
2
0 0
sin cos cos tan 1
cos 2 tan 1
cos 2sin cos cos
tan 1 tan 1 tan
2 tan 1
cos 2 tan 1
x x x x
I dx dx
x x
x x x x
x x
dx d x
x
x x
π π
π π
+ +
= = +
+
+ +
= = +
+
� �
� �
Đ t ặ
( )
2
1
tan tan cos
t x dt d x dx
x
= = =�
Đ i c n ổ ậ
0 0
1
4
x t
x t
= =�
π
= =�
Khi đó
( ) ( ) ( ) ( )
2
1 1 1
0 0 0
1 2 1 2 1 4 2 1 1
1 1
2 1 4
2 1 4 2 1 2 1
t t t t
I dt dt t dt
t t t
+ + − + + + � �
= = = − + +
� �
+ + +
� �
� � �
1
2
0
1 1 1 1 1
3 ln 2 1 4 ln 3 1 ln 3
4 2 4 2 8
I t t t
� � � �
= + + + = + = +
� � � �
� � � �
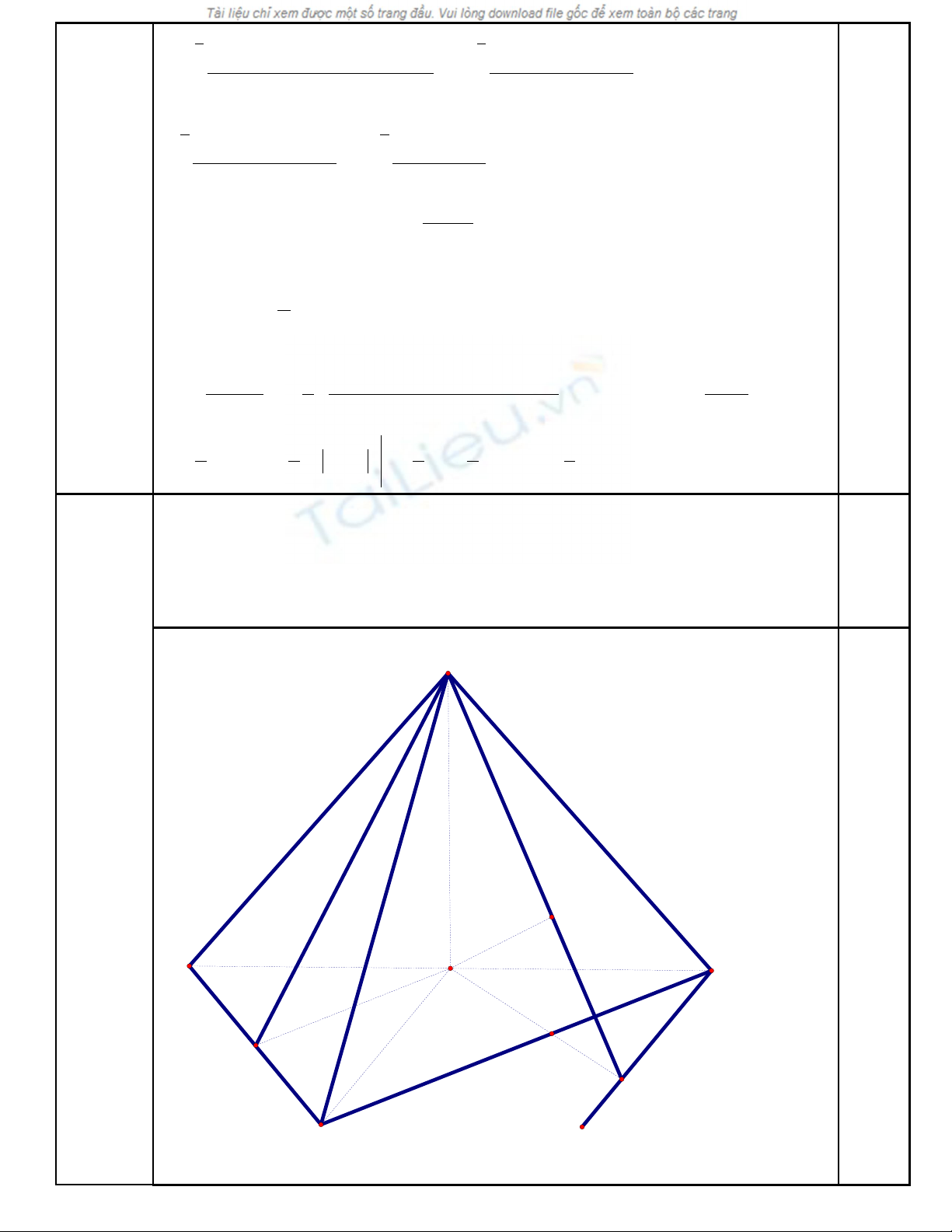
IV Cho hình chóp
.S ABC
có đáy ABC là tam giác vuông t i A, ạ
2 2 .AC BC a
= =
M t ph ng ặ ẳ
( )
SAC
t o v i ạ ớ
( )
ABC
m t góc ộ
0
60
. Hình chi u H c a S lên m tế ủ ặ
ph ng ẳ
( )
ABC
là trung đi m c nh BC. Tính th tích kh i chóp ể ạ ể ố
.S ABC
và
kho ng ả
cách gi a hai đ ng th ng ữ ườ ẳ
HA
và
SB
1,0
a
N
H
C
A
B
S
M
K
ABC
∆
vuông t i A có ạ
ᄊ
ᄊ
0 0
2 , ; 30 , 60BC a AC a B C= = = =
G i N laftrung đi m c a AC Vìọ ể ủ
( )
ᄊ
0
,
60
AC AB AC HN AC SH
AC SHN SNH
⊥ ⊥ ⊥�
⊥ =� �
Trong tam giác
3 3
;
2 2
a a
SNH HN SH= =�
2
3
.
3
2
1 3
.
3 4
ABC
S ABC ABC
a
S
a
V SH S
∆=
= =�
K ẻ
//a AH
(a đi qua B)
( )
// ,HA SB a
G i M là hình chi u c a H lên a và K là hình chi u c a H trên SM khi đíọ ế ủ ế ủ
( )
;HK d HA SB=
Tam giác ACH đ u nên góc ề
ᄊ
0 0 3
60 sin 60 2
a
HBM HM HB= = =�
Trong tam giác SHM ta có
2 2 2
1 1 1 3
4
a
HK
HK HM HS
= + =�
V
Gi i ph ng trình ả ươ
( ) ( )
53 1 2
2
2 1 2 22 1 2 2
1 2 1 2
xxx x x
x x
+
++ = + +
+ +
1,0
3
2 2.2 2.32 2 4 8
1 2 1 4 1 2
x x x x x
x x x
pt + + = + +�+ + +
1 8 32 2 4 8
2
1 2 1 4 1 2
x x x x x
xxx
+ +
+ + =�+++
4 16 64 2 4 8
2
4 8 2 8 2 4
x x x x x x
x x x x x x
+ +
+ + =�+ + +
( ) ( ) ( )
2 2 2
2 4 8 2 4 8
2
4 8 2 8 2 4
x x x x x x
x x x x x x
+ +
+ + =�+ + +
Ta có
( ) ( ) ( ) ( )
( )
2 2 2 2
2 4 8 2 4 8 2 4 8
2
4 8 2 8 2 4 2 2 4 8
x x x x x x x x x
x x x x x x x x x
+ + + +
+ + =
+ + + + +
V y ậ
( ) ( ) ( )
2 2 2
2 4 8 2 4 8 2 4 8
2
4 8 2 8 2 4 4 8 2 8 2 4
x x x x x x x x x
x x x x x x x x x x x x
+ +
+ + = = =�
+ + + + + +
2 4 1 2
1 4 4 8
4 8 2 8 2 4 1 4 0
2 8 1 4 1 2 8 16
4 8 2 4 2 4 1 2
x x x
x x x
x x x x x x x
x x x x x x
x x x x x x x
x
==
+ = +
� � �
+ + + + =� � � �
� � �+ = +
� �
= =
� �
+ + + +�
2,0
1) Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy cho đ ng trònườ
( ) ( ) ( )
2 2
: 3 1 9C x y− + − =
và đ ng th ng ườ ẳ
( )
: 10 0d x y+ − =
. T đi m M trênừ ể
1,0






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



