KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG
ĐỀ THI THỬ TỐT NGHIỆP Môn thi: TOÁN − Giáo dục trung học phổ thông
Đề số 02 Thời gian làm bài: 150 phút, không kể thời gian giao đề
------------------------------ ---------------------------------------------------
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu I (3,0 điểm): Cho hàm số: 3 2
3 3
y x x x
= - +
1) Khảo sát sự biến thiên và vẽ đồ thị
( )
C
của hàm số đã cho.
2) Viết phương trình tiếp tuyến của đồ thị
( )
C
biết tiếp tuyến song song với
đường thẳng có phương trình
3
y x
=.
Câu II (3,0 điểm):
1) Giải phương trình:
6.4 5.6 6.9 0
x x x
- - =
2) Tính tích phân:
0
(1 cos )
p
= +
ò
3) Tìm giá trị lớn nhất và nhỏ nhất của hàm số: 2
( 3)
x
y e x
= -
trên đoạn [–2;2].
Câu III (1,0 điểm):
Hình chóp S.ABC có đáy ABC là tam giác vuông cân (BA = BC), cạnh bên SA
vuông góc với mặt phẳng đáy và có độ dài là
3
a, cạnh bên SB tạo với đáy một
góc 600. Tính diện tích toàn phần của hình chóp.
II. PHẦN RIÊNG (3,0 điểm) Thí sinh chỉ được chọn một trong hai phần dưới đây
1. Theo chương trình chuẩn
Câu IVa (2,0 điêm): Trong không gian với hệ toạ độ Oxyz cho điểm
(2;1;1)
A và hai
đường thẳng
,
1 2 1 2 2 1
: :
1 3 2 2 3 2
x y z x y z
d d
- + + - - +
¢
= = = =
- - -
1) Viết phương trình mặt phẳng
( )
a
đi qua điểm A đồng thời vuông góc với
đường thẳng d
2) Viết phương trình của đường thẳng
D
đi qua điểm A, vuông góc với đường
thẳng d đồng thời cắt đường thẳng
d
¢
Câu Va (1,0 điểm): Giải phương trình sau đây trên tập số phức:
4 2
( ) 2( ) 8 0
z z
- - =
2. Theo chương trình nâng cao
Câu IVb (2,0 điêm): Trong không gian Oxyz cho mp(P) và mặt cầu (S) lần lượt có
phương trình
( ) : 2 2 1 0
P x y z
- + + =
và 2 2 2
( ) : – 4 6 6 17 0
S x y z x y z
+ + + + + =
1) Chứng minh mặt cầu cắt mặt phẳng.
2) Tìm tọa độ tâm và bán kính đường tròn giao tuyến của mặt cầu và mặt phẳng.
Câu Vb (1,0 điểm): Viết số phức sau dưới dạng lượng giác
1
2 2
z
i
=+
---------- Hết ----------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ và tên thí sinh: ........................................ Số báo danh:
...............................................
Chữ ký của giám thị 1: .................................. Chữ ký của giám thị 2:
.................................
x
y
2
2
1I
O1
BÀI GIẢI CHI TIẾT.
Câu I :
3 2
3 3
y x x x
= - +
Tập xác định:
D
=
¡
Đạo hàm: 2
3 6 3
y x x
¢
= - +
Cho 2
0 3 6 3 0 1
y x x x
¢
= Û - + = Û =
Giới hạn: ; lim lim
x x
y y
® - ¥ ® + ¥
= - ¥ = + ¥
Bảng biến thiên x – 1 +
y
¢
+ 0 +
y
– 1 +
Hàm số ĐB trên cả tập xác định; hàm số không đạt cực trị.
6 6 0 1 1
y x x y
¢¢
= - = Û = Þ =
. Điểm uốn là I(1;1)
Giao điểm với trục hoành:
Cho 3 2
0 3 3 0 0
y x x x x
= Û - + = Û =
Giao điểm với trục tung:
Cho
0 0
x y
= Þ =
Bảng giá trị: x 0 1 2
y 0 1 2
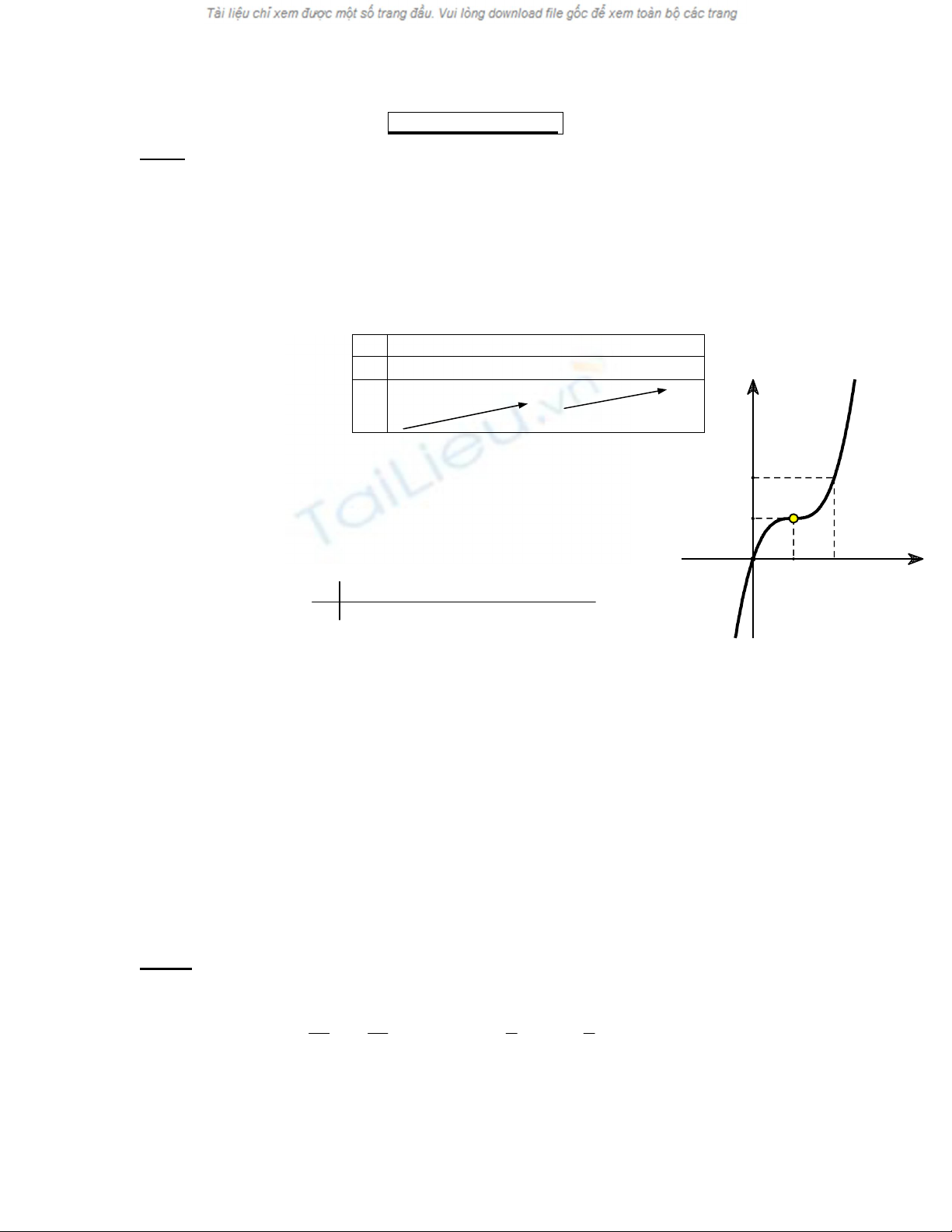
Đồ thị hàm số (như hình vẽ bên đây):
3 2
( ) : 3 3
C y x x x
= - + . Viết của
( )
C
song song với đường thẳng
: 3
y x
D = .
Tiếp tuyến song song với
: 3
y x
D = nên có hệ số góc 0
( ) 3
k f x
¢
= =
Do đó: 2 2 0
0 0 0 0 0
0
3 6 3 3 3 6 0
2
x
x x x x x
é
=
ê
- + = Û - = Û ê
=
ê
ë
Với 0
0
x
=
thì 3 2
0
0 3.0 3.0 0
y
= - + =
và 0
( ) 3
f x
¢
=
nên pttt là:
0 3( 0) 3
y x y x
- = - Û = (loại vì trùng với
D
)
Với 0
2
x
=
thì 3 2
0
2 3.2 3.2 2
y
= - + =
và 0
( ) 3
f x
¢
=
nên pttt là:
2 3( 2) 3 4
y x y x
- = - Û = -
Vậy, có một tiếp tuyến thoả mãn đề bài là:
3 4
y x
= -
Câu II
6.4 5.6 6.9 0
x x x
- - =
. Chia 2 vế pt cho
9
x
ta được
2
4 6 2 2
6. 5. 6 0 6. 5. 6 0
3 3
9 9
x x
x x
x x
æ ö æ ö
÷ ÷
ç ç
÷ ÷
- - = Û - - =
ç ç
÷ ÷
ç ç
è ø è ø (*)