
1. KhAo s6t sU'bi6n thi6n vi ve d6 thi ( C ) cira hdm s6.
2. M ld di€m b6tty o'.tren (C) TicpjuytSn cira ( C) tai M cdt c6c dudng ti€m c4n cria (C) tai A vi B; gqi
I ld giao di6m 2 duong tiQrn c{n. Tim toa dQ M sao cho dudng trdn ngoq.i tirip tam !ij. iae c6 di€n
tichbing 2n
CAu II( 2 di€m):
io'crAo Dvc & DAO TAO HATPHONG
TIIU,ONG THPT THAI PHTEN
i. PHAN CFILN{G CHO TAT CA THi SINH
, '^ -.7
Lau l(z olem) , 2x-3
Lno ham so y = ;-;.( C)
I-L
cos2x + 5 sin
1) Giei phuong trinh :
DE THI THII EAI HQC LAN II IYAM 2011
M6n : TOAN _ KIIoI A
Thdt gian : 180 phrit ( kh6ng nC tndt gtan phdt di )
=- / 2) Gieibdt phuo'ng trinh : -E-- < x+Zt
P - Jn.u)"
I x=2+t
az:ll=-3+3t felR.
I z=t
J7T \
iT- I
)l
cAu rrr ( 1 di€m) : Tinh , 's*(rr, -+)*
d ( J+-*')
c6u IV ( I di6m) : Trong kh6ng gian cho ldng tru dtrr.g ABC.AB:C, eo AB =.a,AC =Za,AA, =2ali vit
ti =120" . Gqi M li.trungditim cira canh CC, . Hdy chfrng minh MB L MAl vi tinh khoing c6ch tir A toi 1.ndt
phing (A.BM ).
Cdu V ( I di€m): Tim ntde hC phuo,ng trinh sau c6 nghiQm v6,ix > ,, {111 .--=-
fVx'+3*^ly'+5=m
rr. PHAN RrENG( 3 diem)
A. Theo chuong trinh chuAn
CduVLa: ( 2 di€m)
l) Trong mat phing v6i h0 trsc tea dQ Oxy cho tam gi6c ABC c6 dinh A rhugc (d):x - 4y -2=0; dudng thing BC
songsongv6'i(d);phuongtrinhdudngcaoBH:x*y*3=0.vdtungdi6mcanhabtaM(f;1).ti-mtqadgcac
dinh A, B, C.
2) Trongkhdnggianv6'ihQtrqctqad0Oxyzchom{tphing(P) :x -2.y+Zz+2=1vdhaidi€mA(4;1;3)vh
B(2;-3;-1).Hdy tim di€m M thuQc (P) sao cho MAz + MB.2 c6 gi6 ni nh6 nh6t .
C6.uVil.a( ldi6rn)
.t
Trongc6c s0 phuczthoamdnphucrngtrinh: liz -Zl=1, -2 - il haytimstiphri'czc6acgumen bingTr
B. Theo chuong trinh ning cao : 4
Cdu VI.b: ( 2di€m):
l) Trong mdtphingOxyclio di6m C( 2;0)vit Elip(E) c6phuongtrinh: t* r= =1. Timcricdi6m A,B thuQc
4'
@) biet ring hai di6rn A,B dOi xn'ng nhau qua tmc irodnh vir tam gi6c ABC ddg.
2) Trong kh6ng gian vdi h€ tga dQ Oxyz, cho hai dudng thdng:
r .x-4 y-I z+5
At | --;- = -; = ---:- Va :
J-i-2
- Viet phuong trinh mflt cdu c6 b6n kfnh nhd nhAt ti6p xirc voi chhai duong thing d, vd d2.
Cdu VII.b: (1 diCm)
Tim gi6 tri nt d€ hdm s6 y =x2 +(m2 -r)x-m2 +m
x-L
zr)
x+- I
3)
tan
cira d6 th! di qua di€m M(l; 5).
d6ng bi6n trdn cdc khoing cria tflp x6c dinh vd ti€m cdn xi€n
www.MATHVN.com
www.mathvn.com
NOi du
oAp Ax vA BIEU DIEM THI THITE C LAN II - KIIOI A -2011
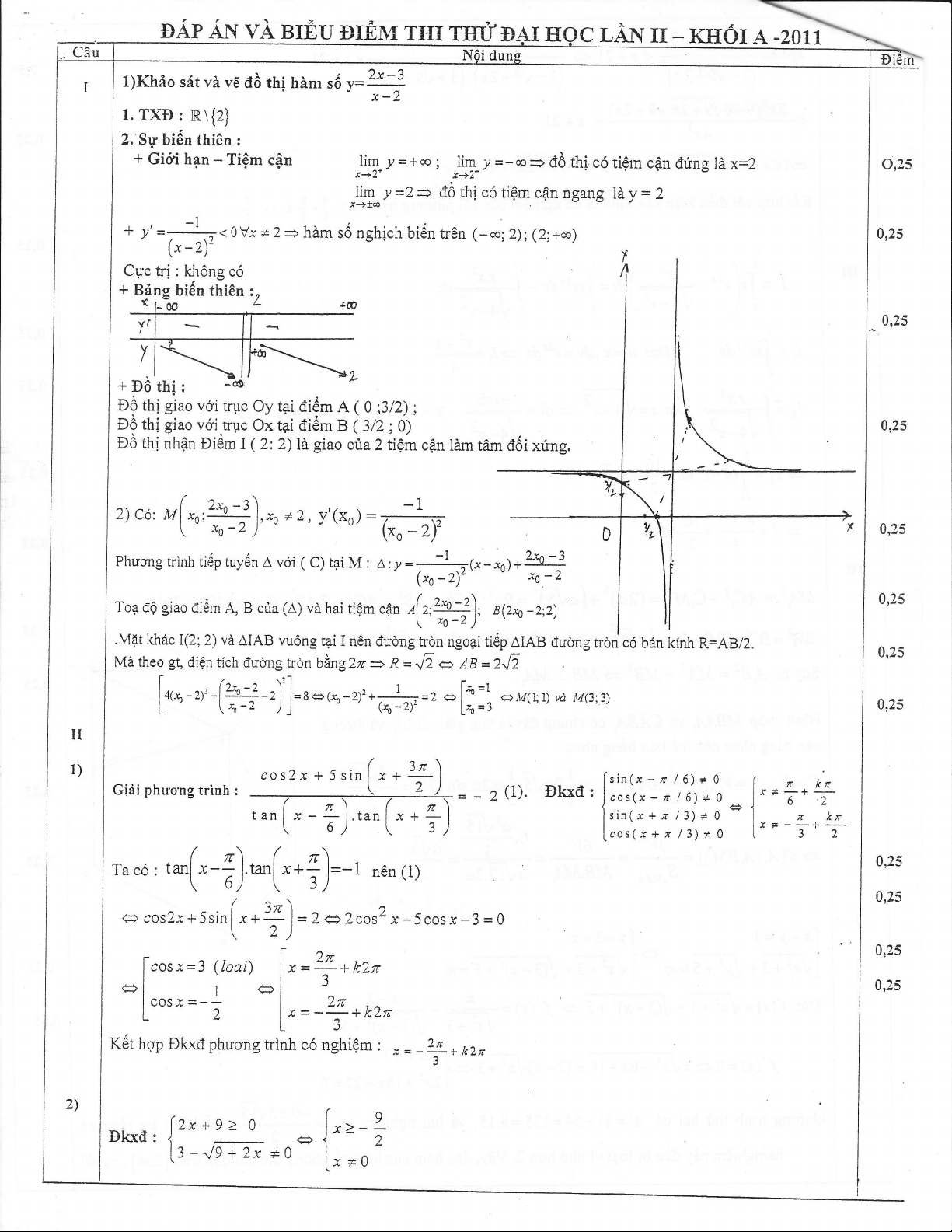
l)Khio sit vi vc a6 tni hirm s5 -2x-3
x-2
1. TXD : R\{z}
2. Su biSn thi6n :
+ Gini hpn - TiQm cgn
+D6thi:
Gitii phu'o'ng trinh :
lim y =a6p ; hn-l_ ! =-q= d6 thi c6 ti6rn cf.1 dirng litx:2
x+2- x-+2-
li+ y =2 = dd thi c6 tiQm cf.n ngang lity = 2
+ y' =--J-< 0 Vx ;e 2 = hdrn sii nghich bi6n tr€n (- -; 2);( 2; +oo)
' (*-2)'
v
E? thigiao vdi trpc Oy tai di6m A(0;312);
D6 thi giao v6i fi'uc Ox t4i di6m B (3/2 ;0)
D6 thi nhdn Di6m I Q:2) lA giao cria 2 tiQm c6n lALrn tAm d6i xilng.
2) co: M[",?;), xs * 2,y'(xo) = 6+
Phuong frinh ti6p ruyt5n A voi ( C) t4i M: t:y =-:! "(r-ro;+?&:1
l*o -2)- xo - z
To4 dq giao didm A, B cta (A) vd hai tidm cfln n(rje4)t Bea -z;z)
\ x\-z )
.Mdt khdc l(?;2) vit AIAB vu6ng t4i I n€n duorg h'dn ngo4i ti6p AIAB duoTrg tr-on cd b6n kinh R:AB/2.
Md theo gt, diQn tich ducng trdn bdng 2x > R= Ji o AB =2Ji
| -, (z*-z r'?l , [x^=1
f <-." - tr' -l?; -, ).] = t -,* - t)' - G+ =, * Ll =', a M(t: t) vd M (3: 3)
cos2x+ssin(x+ =-z(1). Ekxd:
0,25
0,25
0,2s
,un[,-
3n
2
z\ ( r\
-l.tanln+-l
6) l. 3/
f sin(x - a
J cos(x - a
lsin(x+,r
Lcos( r + z
l6)*0
l6)*0
/3)*0
/3)*0
l'*
*] l'*
r ktt
-+ -
62
r kr
--+ -
2t
( zo.1^ ^ )
e costx +5srnIrc* 2 )=2eZcos'
4,25
0,25
4,25
0,25
r ^ ,, ., ; 2r
I cosx=J ltoat) l r=-;+hZ|T
<+l r <+l '
I cosr =-- I 2n
L 2 L"=- : +kt/,
KOt hgp Ekxd phuo'ng trinh c6 ngiriQm :
(g
lx>--
e{ 2
t-
l^
[x + u
Cgc tri : kh6ng c6
+ Bing bi€n thi6n
(tt\(n\
ra c6 : t"[r-AJ ,*["*JJ=-l n6n (t)
x-5cosx-3=0
2r
3
l2x+9> 0
1 ,-
f 3-V9 +2x +0
www.MATHVN.com
www.mathvn.com

^ / --.?
2x'13 + JS +zx)-
t
-t2
r --\2
(3-Je -2x) 13+Je+zx)-
. 2x2
bpte l--------= <x+21
\3-J9+2x)
2x219 +6^19 a2* +9 +2x\
-T
<x+21
e18 +2x + 6.,1; . 2. <2x + 42
Ktit h-op vdi di6u ki6n x6c dinh
x +21
a Jg+z* .4 er<i2
ta c6 nghipm cta b6t phuong trinh ld :lg j
l--<.r< -
l1
la2
[,*o
t- (
I - lxl,2'
Jl
0\
I
I, = [xe?'dx
0
lx*y=3 lt=3-x
?
-
z)
fJ;r' + 3 * rly' *5 = n.' lJx' +: +
D[t /(x) =.,6t;+.ft-rt' * s =
-+)0.='l*r',d*-'l-L*
'14-x') i irl+_*?
Dat u = x,dy =e2t
clx - tr=f
Ir
L='[+- oo, ,=t[4-] +at=P, x= 0=>r =z; x=1=>r=v5
o tf4-x' ^14-*/
2
+ r,= le-f)at=f 4Ji
. e2+l 16
+I=-:''*'--3Jj
43
lv{A,t = A,C,2 +C,Mt =7zo)t *("Ji)' =9a2;BC2 = AB2 + AC2 -zAB.AC3osl20" =7a2 i
BM2 = N +a,f =7d *(rJ t)' =tfr;48 =A4' +zE =(uJs)' +d =zti
Suy ra A,B' = MAr2 + MBz + MB L MAl.
Hinlr ch6p MBAAT vd GABA, c6 chung d6y ld tam gi6c BAA, vd du6ng
cao birrg nhau n€n th6 tich bing nhau
v-t/ -r/ -l - i -.!a.za.sin:20"=ltJE
v = yMB,t,t, = yc'ae,t, = jA4'S^rr. =:2atl 5' 2 3
^ a'JE
=d(A,(A,BM))=#=ffi:m=+
l(r 1
. - A. I
\-
,f(:*1\s=,,
tt, , X X-3
:.:,=:-:
.J x' +3 ./1: - x;'? + s
.f '(x)=6a;"nf4afi =(3-DJx'1 +3 o{"-'=t
l2x" +I\x-27 =0
Phuong trinh thft hai c6 A,=81+54=135=9.15, vd hai nghiQm: ,r=2Y.
hainghi€m ndy ddu bi loai vi nh6 hon 2. vfy, dg.o hiim cria hdm s6 kh6ng rhe d6i
O5 t<icm tra ring cd
d6u tr6n 12;.o) , rigodi
www.MATHVN.com
www.mathvn.com

VIa
r)
VIb
1)
ra f '(3) > 0 n6n .f '(*) > A,Yx2Z .
Do d6, gi6 tri nh6 nirdt ciia f (x) khix>2
phuong trinh d6 cho c6 nghi€m (vdi
liL f (2)=^11 +Je .Ctng d6 th6y tyif Q)= co , Tir. d6 suy ra: h€
x>2) khi vd chi khi *>"G *J7 .
-4a-l -a+I 2 .( 2 2\
1 =___ €d= __= ,[_: , _ j )
817
__0 _+b
DoBC//(il.'+=+
A( 4a+2i a) suy ra
eUe+a-1;-a+1). Do AM LBH
M tdnunghek,q,c ,a" c(2,!\
l3'? /
\' - /
:x+ y +3 =0 n1n:
Be (d):x+y+3=0 n€n B(b;-b-3)
e b=-4e B(-4;l)
e,Kr1f 4y-lf =17 +1o*y
<> ir - -2y -1* z=(-Zy -1) + yi
-(q
1'7 \
=BC I Y-n :1-+b l.
\3 '3 )
Gqi I ld trung ditSm AB suy ra I( 3 ;-1 ;1). Ap dgng hg thric trung ruy6n ftong tam gi6c MAB n6n ta c6 :
MAz +IvB2 =2742 *AB2
2
+ MA2 + W2 nhdnhd e tufr nnl nndi e l,fr L (p)
ndn M ld hinh chi6u ctia i tr€n (p)
Gqi (d) ld duong thing vu6ng g6c v6'i (p) va di qua I suy ra phuong trinh cria (d) Id :
M ld. giao di6m crla (d) va @) n6n ta c6 M(2;1;-1)
Ddt z =x+ yi(x,y e R)
li(x + yi)- :l =l(x + yi) - z- rl o l-y - 3 + xil=le - 2) + (y - \rl
x-3 y+1 z -1
-=_=_
1aa
l---z:]--=r^4=4 (i)
Acgumencio,M)gfLellcz:'-,,"' *" 4 Jz
t l-----f- =r-4=-l {3)
l^lt-zy -1)' + y' a 'Jz
Ctng Q)vd (Z)cho ta y - -1, thi tai th1amdncd 1t1vd 1zy
Ydy z =1-i
Goi A(x;y)=B(x;-y). A,B phdn bi|tn€n y* 0. Ae(
Do C (2;0) n€n ACAB cdn rai C.
=ACAB ftieCA=AB €(z-x)t + t, =4x2 (2)
lx=-2 >y=0(loqi)
Gi;ih€(DvA e)ta itdc: i to ' , iru
L^ - 13 -'Y - 6'76
n,,.n*^e r\ .-,\(to tz) lto -tz)
ta co z dtem A,b can rm ta l,'; n I "" lO; n )
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
4,25
www.MATHVN.com
www.mathvn.com

(^
I Y: l-Lf
I
a, : I I = -3 + 3r = (d, di qua M r(2; -3:0) c6 WCp ur(I; 3; t).
I z =t
ra rttlu : ,41.M/14, =60 +0+ dr;drch/o nhau.Goi MN litfoqn vutng g6cchung cila d,;d,
rh1 Mdt ct cobenkinh nh| nh{t trcl rhe void,d, titmit ciu ahig tciin uw
M e d,+ M(4+3r;I-r;-5 -Zt) ; N e dr+ N(Z+ t,;-3 +3t,;r)
I tutY .^ =O l-tqr -2t'=lZ lr = -I
\m.r,=o o \ ,r* rtt'=9o {r'=t +M(r;2;-3);N(3;0;1)
M{t ctu &to-ng ki;h MN cJ ftn r (2;1; -t1 c J u ah nin n = J e
P hndng rriih mdt c d7t t d : (x - 2)' + (y- 1)t + (z + I)2 = 6
TiQm cAn xi€n (A): y = x + m2 .
t,m
y =1----;>0,Vx+1:>
(x -r)'
a
Y4y m:_Z
0,25
TU M(1; 5) e (A):+ m = 12.
*2 -2* +1-m
{t -1)2
<+A'<0 em<O
>OVx *Ie x2 -2x+1-m>0Y x +1
www.MATHVN.com
www.mathvn.com






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



