Đề thi thử ĐH môn Toán khối A (2009-2010)

Chia sẻ: Nguyen Phuc | Ngày: | Loại File: DOC | Số trang:6

Thêm vào BST

Báo xấu

269
lượt xem 60
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tham khảo tài liệu 'đề thi thử đh môn toán khối a (2009-2010)', tài liệu phổ thông, ôn thi đh-cđ phục vụ nhu cầu học tập, nghiên cứu và làm việc hiệu quả

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi thử ĐH môn Toán khối A (2009-2010)

ĐỀ THI THỬ ĐẠI HỌC NĂM 2009-2010. Môn: Toán A. Thời gian: 180 phút ( Không kể giao đề). I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm). 2x + 4 Câu I (2 điểm): Cho hàm số y = . 1− x 1) Khảo sát và vẽ đồ thị ( C ) của hàm số trên. 2) Gọi (d) là đường thẳng qua A( 1; 1 ) và có hệ số góc k. Tìm k sao cho (d) cắt ( C ) tại hai điểm M, N và MN = 3 10 . Câu II (2 điểm): 1) Giải phương trình: sin 3 x − 3sin 2 x − cos 2 x + 3sin x + 3cos x − 2 = 0 .  x 2 + y 2 + xy + 1 = 4 y 2) Giải hệ phương trình:  .  y( x + y) = 2 x + 7 y + 2 2 2 π Câu III (1 điểm): Tính tích phân: I = 3sin x − 2 cos x dx 2 ∫ (sin x + cos x)3 0 Câu IV (1 điểm): Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật với SA vuông góc với đáy, G là trọng tâm tam giác SAC, mặt phẳng (ABG) cắt SC tại M, cắt SD tại N. Tính thể tích của khối đa diện MNABCD biết SA=AB=a và góc hợp bởi đường thẳng AN và mp(ABCD) bằng 300 . Câu V (1 điểm): Cho các số dương a, b, c : ab + bc + ca = 3. 1 1 1 1 Chứng minh rằng: + + ≤ . 1 + a (b + c) 1 + b (c + a) 1 + c (a + b) abc 2 2 2 II. PHẦN RIÊNG (3 điểm) (Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc phần 2)). 1. Theo chương trình Chuẩn : Câu VI.a (2 điểm): 1) Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn hai đường tròn (C ) : x 2 + y 2 – 2 x – 2 y + 1 = 0, (C ') : x 2 + y 2 + 4 x – 5 = 0 cùng đi qua M(1; 0). Viết phương trình đường thẳng qua M cắt hai đường tròn (C ), (C ') lần lượt tại A, B sao cho MA= 2MB. 2) Trong không gian với hệ tọa độ Oxyz, hãy xác định toạ độ tâm và bán kính đường tròn ngoại tiếp tam giác ABC, biết A(-1; 0; 1), B(1; 2; -1), C(-1; 2; 3). Câu VII.a (1 điểm): Khai triển đa thức: (1 − 3 x) = a0 + a1 x + a2 x + ... + a20 x . Tính tổng: S = a0 + 2 a1 + 3 a2 + ... + 21 a20 . 20 2 20 2. Theo chương trình Nâng cao : Câu VI.b (2 điểm) 1) Trong mặt phẳng với hệ toạ độ Oxy, hãy viết phương trình các cạnh của tam giác ABC biết trực tâm H (1;0) , chân đường cao hạ từ đỉnh B là K (0; 2) , trung điểm cạnh AB là M (3;1) . x y z 2) Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng: (d1 ) : = = và 1 1 2 x +1 y z −1 (d 2 ) : = = . −2 1 1 Tìm tọa độ các điểm M thuộc (d1 ) và N thuộc (d 2 ) sao cho đường thẳng MN song song với mặt phẳng ( P) : x – y + z + 2010 = 0 độ dài đoạn MN bằng 2.  2 log1− x (− xy − 2 x + y + 2) + log 2+ y ( x 2 − 2 x + 1) = 6  Câu VII.b (1 điểm): Giải hệ phương trình  log1− x ( y + 5) − log 2+ y ( x + 4)  =1
………………………………….....................HẾT…………………………………………………… Câu Phần Nội dung Điể m I Làm đúng, đủ các bước theo Sơ đồ khảo sát hàm số cho điểm tối đa. 1,0 (2,0 1(1,0 ) ) 2(1,0 Từ giả thiết ta có: (d ) : y = k ( x − 1) + 1. Bài toán trở thành: Tìm k để hệ phương trình ) 0,25 sau có hai nghiệm ( x1 ; y1 ), ( x2 ; y2 ) phân biệt sao cho ( x2 − x1 ) + ( y2 − y1 ) = 90(*) 2 2  2x + 4  = k ( x − 1) + 1 kx 2 − (2k − 3) x + k + 3 = 0  −x +1 ( I ) . Ta có: ( I ) ⇔   y = k ( x − 1) + 1  y = k ( x − 1) + 1  Dễ có (I) có hai nghiệm phân biệt khi và chỉ khi phương trình 3 kx 2 − (2k − 3) x + k + 3 = 0(**) có hai nghiệm phân biệt. Khi đó dễ có được k ≠ 0, k < . 8 Ta biến đổi (*) trở thành: (1 + k ) ( x2 − x1 ) = 90⇔ (1 + k )[( x2 + x1 ) − 4 x2 x1 ] = 90(***) 2 2 2 2 2k − 3 k +3 Theo định lí Viet cho (**) ta có: x1 + x2 = , x1 x2 = , thế vào (***) ta có 0,5 k k phương trình: 8k 3 + 27k 2 + 8k − 3 = 0 ⇔ (k + 3)(8k 2 + 3k − 1) = 0 −3 + 41 −3 − 41 ⇔ k = −3, k = , k= . 16 16 KL: Vậy có 3 giá trị của k thoả mãn như trên. 0,25 Câu Phần Nội dung Điể m II sin 3 x − 3sin 2 x − cos 2 x + 3sin x + 3cos x − 2 = 0 ⇔ (2,0 1(1,0) (sin 3 x + sin x) + 2sin x − 3sin 2 x − (cos 2 x + 2 − 3cos x ) = 0 0,25 ) ⇔ 2sin 2 x.cos x + 2sin x − 6.sin .cos x − (2 cos 2 x − 3cos x + 1) = 0 ⇔ 2sin x.cos 2 x + 2sin x − 6.sin .cos x − (2 cos 2 x − 3cos x + 1) = 0  1  sin x = 2  0,25 ⇔ (2sin x − 1)(2 cos 2 x − 3cos x + 1) = 0 ⇔  cos x = 1  1 cos x =  2  π 1  x = 6 + k 2π +) sin x = ⇔  , (k ∈ Z ). 2  x = 5π + k 2π   6  π  x = + k 2π 1 3 +) cos x = ⇔  , (k ∈ Z ). 2  x = − π + k 2π   3 cos x = 1 ⇔ x = k 2π , (k ∈ Z ). 0,25 +) KL:Vậy phương trình có 5 họ nghiệm như trên. 0,25
2(1,0)  x2 + 1  +x+ y =4  x 2 + y 2 + xy + 1 = 4 y  y Dễ thấy y ≠ 0 , ta có:  ⇔ . 0,25  y( x + y) = 2 x + 7 y + 2 2 2 ( x + y ) 2 − 2 x + 1 = 7 2   y x2 + 1  u+v = 4  u = 4−v  v = 3, u = 1 Đặ t u = , v = x + y ta có hệ:  2 ⇔ 2 ⇔ 0,25 y v − 2u = 7 v + 2v − 15 = 0  v = −5, u = 9 +) Với v = 3, u = 1 ta có hệ:  x2 + 1 = y  x2 + 1 = y  x2 + x − 2 = 0  x = 1, y = 2  ⇔ ⇔ ⇔ . 0,25 x+ y =3  y = 3− x  y = 3− x  x = −2, y = 5  x2 + 1 = 9 y  x2 + 1 = 9 y  x 2 + 9 x + 46 = 0 +) Với v = −5, u = 9 ta có hệ:  ⇔ ⇔ , hệ  x + y = −5  y = −5 − x  y = −5 − x này vô nghiệm. KL: Vậy hệ đã cho có hai nghiệm: ( x; y ) = {(1; 2), (−2; 5)}. 0,25 Câu Phần Nội dung Điể m III π π π 0,25 (1,0 Đặ t x = − t ⇒ dx = −dt , x = 0 ⇒ t = , x = ⇒ t = 0. 2 2 2 ) π π π Suy ra: I = 3sin x − 2 cos x dx = 3cos t − 2sin t dt = 3cos x − 2sin x dx (Do tích phân 2 2 2 ∫ (sin x + cos x)3 ∫ (cos t + sin t )3 ∫ (cos x + sin x)3 0 0 0 0,25 không phụ thuộc vào kí hiệu cảu biến số). π π π Suy ra: 2 I = I + I = 3sin x − 2 cos x dx + 3cos x − 2sin x dx = 2 2 2 1 ∫ (sin x + cos x)3 ∫ (cos x + sin x)3 ∫ (sin x + cos x)2 dx = 0 0 0 π π 2 1 1 2 1  π 1  ππ =∫ dx = ∫ d  x −  = tan  x −  2 = 1 . KL: Vậy I = 1 . 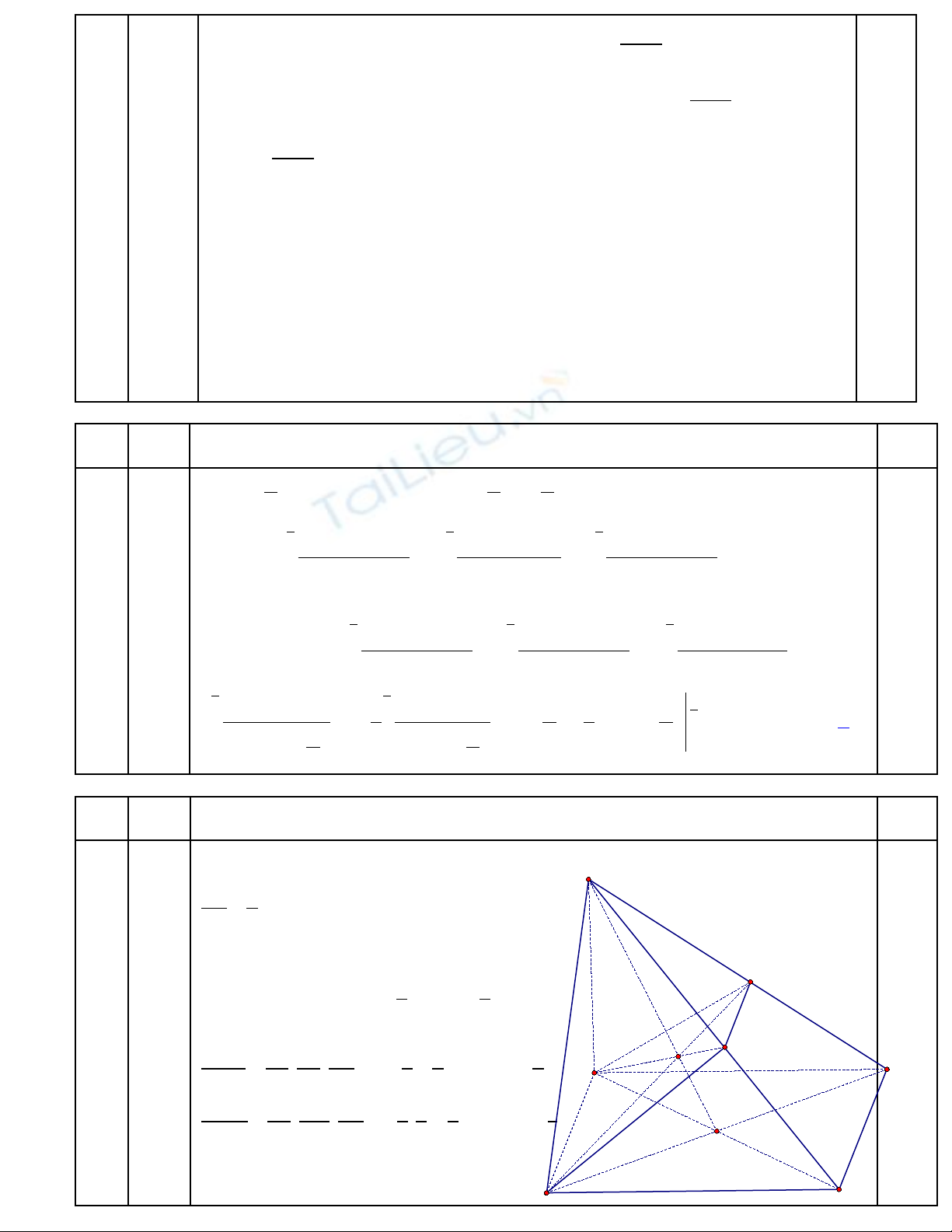0,5 0 2 cos 2  x − π  π cos 2  x −   20 4 2  4 0 2    4  4 Câu Phần Nội dung Điể m IV + Trong mp(SAC) kẻ AG cắt SC tại M, trong mp(SBD) kẻ BG cắt SD tại N. (1,0 + Vì G là trọng tâm tam giác ABC nên dễ có S ) SG 2 = suy ra G cũng là trọng tâm tam giác SBD. SO 3 Từ đó suy ra M, N lần lượt là trung điểm của 0,25 SC, SD. N 1 1 + Dễ có: VS . ABD = VS . BCD = VS . ABCD = V . 2 2 Theo công thức tỷ số thể tích ta có: M G VS . ABN SA SB SN 1 1 1 D = . . = 1.1. = ⇒ VS . ABN = V A VS . ABD SA SB SD 2 2 4 VS . BMN SB SM SN 1 1 1 1 = . . = 1. . = ⇒ VS . ABN = V O VS . BCD SB SC SD 2 2 4 8 Từ đó suy ra: B C 0,25
3 VS . ABMN = VS . ABN + VS .BMN = V . 8 1 + Ta có: V = SA.dt ( ABCD ) ; mà theo giả thiết SA ⊥ ( ABCD) nên góc hợp bởi AN với 3 · mp(ABCD) chính là góc NAD , lại có N là trung điểm của SC nên tam giác NAD cân tại SA · · N, suy ra NAD = NDA = 300. Suy ra: AD = =a 3. tan 300 1 1 3 3 Suy ra: V = SA.dt ( ABCD) = a.a.a 3 = a . 3 3 3 3 5 5 3a 3 0,5 Suy ra: thể tích cần tìm là: VMNABCD = VS . ABCD − VS . ABMN = V − V = V = . 8 8 24 Câu Phần Nội dung Điể m V Áp dụng BĐT Cauchy cho 3 số dương ta có: 3 = ab + bc + ca ≥ 3 3 (abc) 2 ⇒ abc ≤ 1 . 0,25 (1,0 ) 1 1 Suy ra: 1 + a (b + c ) ≥ abc + a (b + c) = a( ab + bc + ca ) = 3a ⇒ ≤ 2 2 (1). 1 + a (b + c) 3a 2 1 1 1 1 0,25 Tương tự ta có: ≤ (2), ≤ (3). 1 + b (c + a ) 3b 2 1 + c (a + b) 3c 2 Cộng (1), (2) và (3) theo vế với vế ta có: 1 1 1 1 1 1 1 ab + bc + ca 1 + + ≤ ( + + )= = W. 1 + a (b + c) 1 + b (c + a) 1 + c (a + b) 3 c b c 2 2 2 3abc abc Dấu “=” xảy ra khi và chỉ khi abc = 1, ab + bc + ca = 3 ⇒ a = b = c = 1, (a, b, c > 0). 0,5 Câu Phần Nội dung Điể m VI + Gọi tâm và bán kính của (C), (C’) lần lượt là I(1; 1) , I’(-2; 0) và R = 1, R ' = 3 , đường a 1(1,0 thẳng (d) qua M có phương trình a ( x − 1) + b( y − 0) = 0 ⇔ ax + by − a = 0, ( a 2 + b 2 ≠ 0)(*) 0,25 (2,0 ) . ) + Gọi H, H’ lần lượt là trung điểm của AM, BM. Khi đó ta có: MA = 2MB ⇔ IA2 − IH 2 = 2 I ' A2 − I ' H '2 0,25 ⇔ 1 − ( d ( I ;d ) ) = 4[9 − ( d ( I ';d ) ) ] , 2 2 IA > IH . 9a 2 b2 ⇔ 4 ( d ( I ';d ) ) − ( d ( I ;d ) ) = 35 ⇔ 4. 2 2 − 2 = 35 a 2 + b2 a + b2 0,25 36a − b 2 2 ⇔ = 35 ⇔ a 2 = 36b 2 a +b 2 2  a = −6 Dễ thấy b ≠ 0 nên chọn b = 1 ⇒  . 0,25  a=6 Kiểm tra điều kiện IA > IH rồi thay vào (*) ta có hai đường thẳng thoả mãn. uuur uuu r 2(1,0 + Ta có: AB = (2; 2; −2), AC = (0; 2; 2). Suy ra phương trình mặt phẳng trung trực của 0,25 ) AB, AC là: x + y − z − 1 = 0, y + z − 3 = 0. r uuu uuu r r + Vecto pháp tuyến của mp(ABC) là n =  AB, AC  = (8; −4; 4). Suy ra (ABC):   2x − y + z +1 = 0 . 0,25
 x + y − z −1 = 0 x = 0   + Giải hệ:  y + z − 3 = 0 ⇒  y = 2 . Suy ra tâm đường tròn là I (0; 2;1). 2 x − y + z + 1 = 0  z = 1 0,5   Bán kính là R = IA = (−1 − 0) 2 + (0 − 2) 2 + (1 − 1) 2 = 5. Câu Phần Nội dung Điể m VII 0,25 + Ta có: ( x (1 − 3x ) 20 ) ′ = a0 + 2a1 x + 3a2 x 2 + ... + 21a20 x 20 . .a (1,0) ⇔ (1 − 3x ) 20 − 60 x (1 − 3 x)19 = a0 + 2a1 x + 3a2 x 2 + ... + 21a20 x 20 (*). 0,25 0,25 Nhận thấy: ak x = ak (− x) do đó thay x = −1 vào cả hai vế của (*) ta có: k k S = a0 + 2 a1 + 3 a2 + ... + 21 a20 = 422 . 0,25 Câu Phần Nội dung Điể m VI + Đường thẳng AC vuông góc với HK nên nhận uuur A b 1(1,0 HK = (−1; 2) làm vtpt và AC đi qua K nên (2,0 ) ( AC ) : x − 2 y + 4 = 0. Ta cũng dễ có: ) 0,25 ( BK ) : 2 x + y − 2 = 0 . + Do A ∈ AC , B ∈ BK nên giả sử M A(2a − 4; a ), B (b; 2 − 2b). Mặt khác M (3;1) là K trung điểm của AB nên ta có hệ: H  2a − 4 + b = 6  2a + b = 10 a = 4  ⇔ ⇔ .  a + 2 − 2b = 2  a − 2b = 0 b = 2 0,5 Suy ra: A(4; 4), B (2; − 2). C B uuu r + Suy ra: AB = (−2; − 6) , suy ra: ( AB ) : 3x − y − 8 = 0 . uuu r + Đường thẳng BC qua B và vuông góc với AH nên nhận HA = (3; 4) , suy ra: ( BC ) : 3 x + 4 y + 2 = 0. KL: Vậy : ( AC ) : x − 2 y + 4 = 0, ( AB ) : 3 x − y − 8 = 0 , ( BC ) : 3 x + 4 y + 2 = 0. 0,25 2(1,0 + M , N ∈ (d1 ), (d 2 ) nên ta giả sử ) uuuu r 0,25 M (t1 ; t1 ; 2t1 ), N (−1 − 2t2 ; t2 ;1 + t2 ) ⇒ NM = (t1 + 2t2 + 1; t1 − t2 ; 2t1 − t2 − 1) . uu uuuu r r + MN song song mp(P) nên: nP .NM = 0 ⇔ 1.(t1 + 2t2 + 1) − 1.(t1 − t2 ) + 1(2t1 − t2 − 1) = 0 uuuur 0,25 ⇔ t2 = −t1 ⇒ NM = ( −t1 + 1; 2t1 ;3t1 − 1) .  t1 = 0 + Ta có: MN = 2 ⇔ (−t1 + 1) + (2t1 ) + (3t1 − 1) = 2 ⇔ 7t − 4t1 = 0 ⇔  2 2 2 2 . t1 = 4 1  7 0,25 4 4 8 1 4 3 + Suy ra: M (0; 0; 0), N (−1; 0;1) hoặc M ( ; ; ), N ( ; − ; ) . 7 7 7 7 7 7 + Kiểm tra lại thấy cả hai trường hợp trên không có trường hợp nào M ∈ ( P ). 0,25 KL: Vậy có hai cặp M, N như trên thoả mãn. Câu Phần Nội dung Điể m
VII. − xy − 2 x + y + 2 > 0, x 2 − 2 x + 1 > 0, y + 5 > 0, x + 4 > 0 0,25 b + Điều kiện:  (I ) .  0 < 1 − x ≠ 1, 0 < 2 + y ≠ 1 (1,0) 2 log1− x [(1 − x)( y + 2)] + 2 log 2+ y (1 − x) = 6  + Ta có: ( I ) ⇔  log1− x ( y + 5) − log 2+ y ( x + 4)  =1 log1− x ( y + 2) + log 2+ y (1 − x ) − 2 = 0 (1)  ⇔ log1− x ( y + 5) − log 2+ y ( x + 4) = 1 (2). 0,25  1 + Đặt log 2+ y (1 − x ) = t thì (1) trở thành: t + − 2 = 0 ⇔ (t − 1) = 0 ⇔ t = 1. 2 t Với t = 1 ta có: 1 − x = y + 2 ⇔ y = − x − 1 (3). Thế vào (2) ta có: −x + 4 −x + 4 log1− x (− x + 4) − log1− x ( x + 4) = 1 ⇔ log1− x =1⇔ = 1 − x ⇔ x2 + 2 x = 0 x+4 x+4  x=0  y = −1 ⇔ . Suy ra:  .  x = −2  y =1 0,25 + Kiểm tra thấy chỉ có x = −2, y = 1 thoả mãn điều kiện trên. Vậy hệ có nghiệm duy nhất x = −2, y = 1 . 0,25