SỞ GD-ĐT PHÚ THỌ
TRƯỜNG T.H.P.T LONG CHÂU SA ÐỀ THI THỬ ĐẠI HỌC
NĂM HỌC: 2010-2011
Môn thi : TOÁN
THỜI GIAN LÀM BÀI:150 PHÚT(không kể thời gian giao đề)
PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)
Câu I:(2 điểm)
Cho hàm số : 1x2
1x
y
(C)
1. Khảo sát và vẽ đồ thị hàm số.
2. Viết phương trình tiếp tuyến với (C), biết tiếp tuyến đó đi qua giao điểm của đường tiệm cận và trục Ox.
Câu II:(2 điểm)
1. Giải phương trình:
sin 2 cos2
cot
cos sin
x x
tgx x
x x
2. Giải phương trình:
1
xlog1
4
3logxlog2
3
x93
Câu III: (2 điểm)
1.Tính nguyên hàm: sin 2
( )
3 4 sin 2
xdx
F x
x cos x
2.Giải bất phương trình:
x x x
Câu IV: (1 điểm)
Trong mặt phẳng Oxy cho tam giác ABC có trọng tâm G(2, 0) biết phương trình các cạnh AB, AC theo thứ
tự là 4x + y + 14 = 0; 02y5x2
. Tìm tọa độ các đỉnh A, B, C.
PHẦN RIÊNG (3 điểm)
Chú ý:Thí sinh chỉ được chọn bài làm ở một phần nếu làm cả hai sẽ không được chấm
A. Theo chương trình chuẩn
Câu Va :
1. Tìm hệ số của x8 trong khai triển (x2 + 2)n, biết: 49CC8A 1
n
2
n
3
n .
2. Cho đường tròn (C): x2 + y2 – 2x + 4y + 2 = 0.
Viết phương trình đường tròn (C') tâm M(5, 1) biết (C') cắt (C) tại các điểm A, B sao cho 3AB .
B. Theo chương trình Nâng cao
Câu Vb:
1. Giải phương trình :
21x2log1xlog 3
2
3
2. Cho hình chóp SABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáy hình chóp.
Cho AB = a, SA = a 2. Gọi H và K lần lượt là hình chiếu vuông góc của A lên SB, SD.
Chứng minh SC (AHK) và tính thể tích khối chóp OAHK.
………………… …..………………..Hết…………………………………….
(Cán bộ coi thi không giải thích gì thêm)
HƯỚNG DẪN CHẤM MÔN TOÁN
Câu ý Nội Dung Điểm
I 2
1 Khảo sát hàm số (1 điểm) 1
TXĐ: D = R\ {-1/2}
Sùự Biến thiên:
,
2
30
2 1
y x D
x
Nên hàm số nghịch biến trên 1 1
( ; ) ( ; )
2 2
v a
0,25
+ Giới hạn ,tiệm cận:
1
2
lim
x
y
1
2
lim
x
y

ĐTHS có tiẹm cận đứng : x = -1/2
1
lim
2
x
y

1
lim
2
x
y

ĐTHS có tiệm cận ngang: y = -1/2
0,25
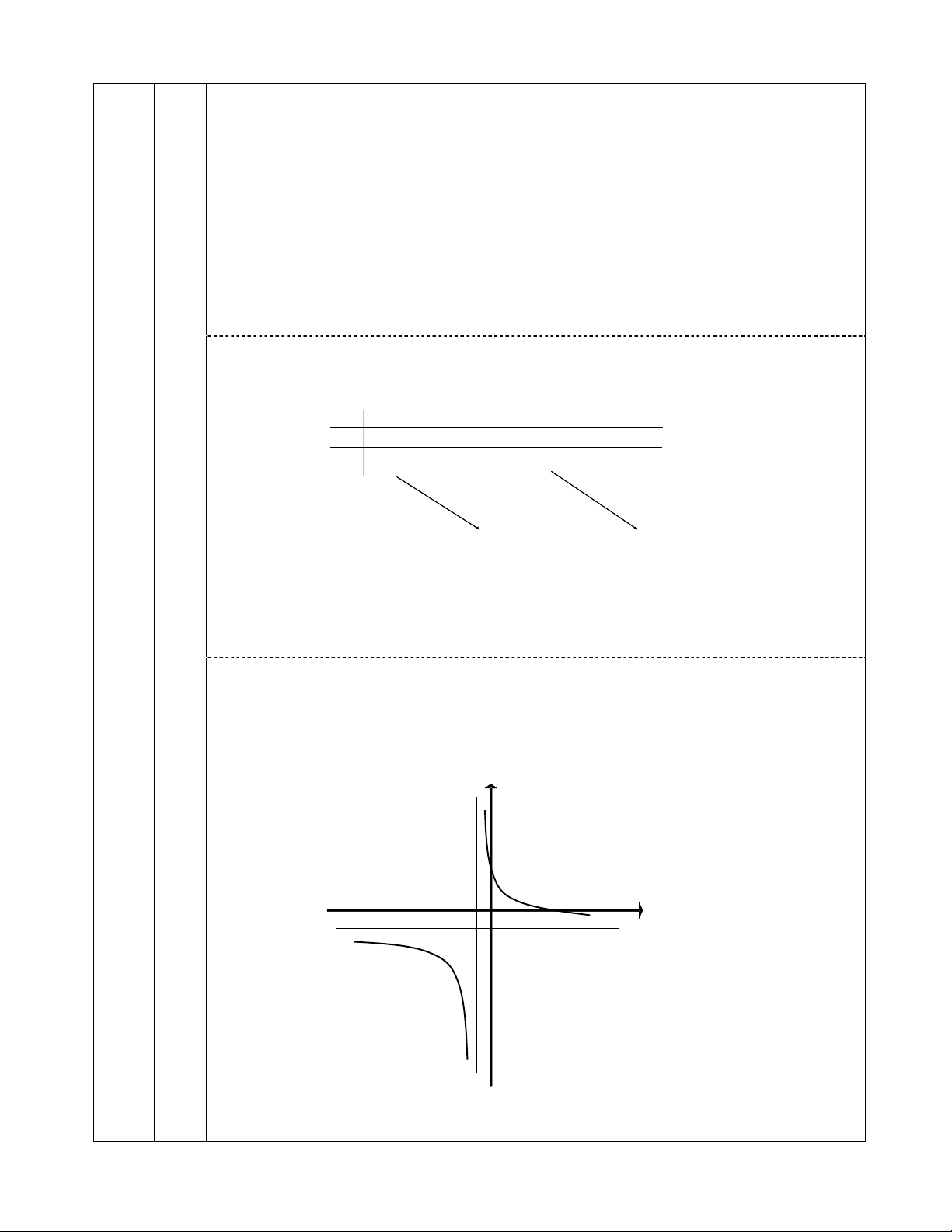
+ Bảng biến thiên:
0,25
Đồ Thị :
0,25
y
x
0
I
-
1/2
1
1
-
1
/2
x
y
’
y
-
1
/2
-
-
-1/2
-
1
/2
2
Giao điểm của tiệm cận đứng với trục Ox là
0,
2
1
A
Phương trình tiếp tuyến () qua A có dạng
2
1
xky
() tiếp xúc với (C) /
x 1 1
k x
2x 1 2
x 1
k co ù nghieäm
2x 1
0,25
)2( k
1x2
3
)1(
2
1
xk
1x2
1x
2
Thế (2) vào (1) ta có pt hoành độ tiếp điểm là
2
1
3 x
x 1
2
2x 1
2x 1
0,25
1
(x 1)(2x 1) 3(x )
2
và
1
x
2
3
x 1
2
5
x
2
. Do đó 12
1
k
0,25
Vậy phương trình tiếp tuyến cần tìm là:
1 1
y x
12 2
0,25
II 2
1
1. Giải phương trình: gxcottgx
xsin
x2cos
xcos
x2sin (1)
(1) xsin
xcos
xcos
xsin
xcosxsin
xsinx2sinxcosx2cos
xcosxsin
xcosxsin
xcosxsin
xx2cos 22
0,25
cosx cos2x sin2x 0
2
2cos x cosx 1 0 sin2x 0
0,25
1
cosx ( cosx 1 :loaïi vì sinx 0)
2
0,25
2k
3
x 0,25
2
2. Phương trình:
1
xlog1
4
3logxlog2
3
x93
(1)
(1)
1
xlog1
4
x9log
1
xlog2
33
3
0,25
1
xlog1
4
xlog2
xlog2
33
3
đặt: t = log3x
0,25
thành 2
2 t 4
1 t 3t 4 0
2 t 1 t
0,25