Trang 1/6 – Mã đề 101
TRƯỜNG THPT CHUYÊN BẮC NINH
TỔ TOÁN TIN
ĐỀ THI THỬ THPT QUỐC GIA LẦN 1
NĂM HỌC 2018 - 2019
MÔN: Toán
Thời gian làm bài : 90 Phút (không kể thời gian giao đề)
(Đề thi gồm có 06 trang)
Họ tên : ............................................................... Số báo danh : ...............................
Câu 1: Hàm số 32
35yx x đồng biến trên khoảng nào dưới đây?
A. (0;2) B. (0; ) C. (;2)
D. (;0) và (2; )
Câu 2: Trong các dãy số sau đây, dãy số nào là một cấp số cộng?
A. 21
n
un
, 1n B. 2n
n
u, 1n C. 1
n
un
, 1n D. 23
n
un, 1n
Câu 3: Hàm số có đạo hàm bằng 2
1
2x
x
là:
A.
3
3
22x
yx
B.
31x
y
x
C.
3
33
x
x
yx
D.
351
x
x
yx

Câu 4: Nếu hàm số ()yfxcó đạo hàm tại 0
thì phương trình tiếp tuyến của đồ thị hàm số tại điểm
00 0
(;())
M
xfx là
A. '
00
()( ) ( )
yf
xx x
f
x
B. '
00
()( ) ( )
yf
xx x
f
x
C. '
00 0
()( ) ()yfxxx fx
D. '
00 0
()( ) ()yfxxx fx
Câu 5: Giới hạn
222
lim 2
x
x
x


bằng
A.  . B. 1. C.
. D. 1.
Câu 6: Cho tập hợp S gồm 20 phần tử. Tìm số tập con gồm 3 phần tử của S.
A. 3
20
A
B. 3
20
C C. 60 D. 3
20
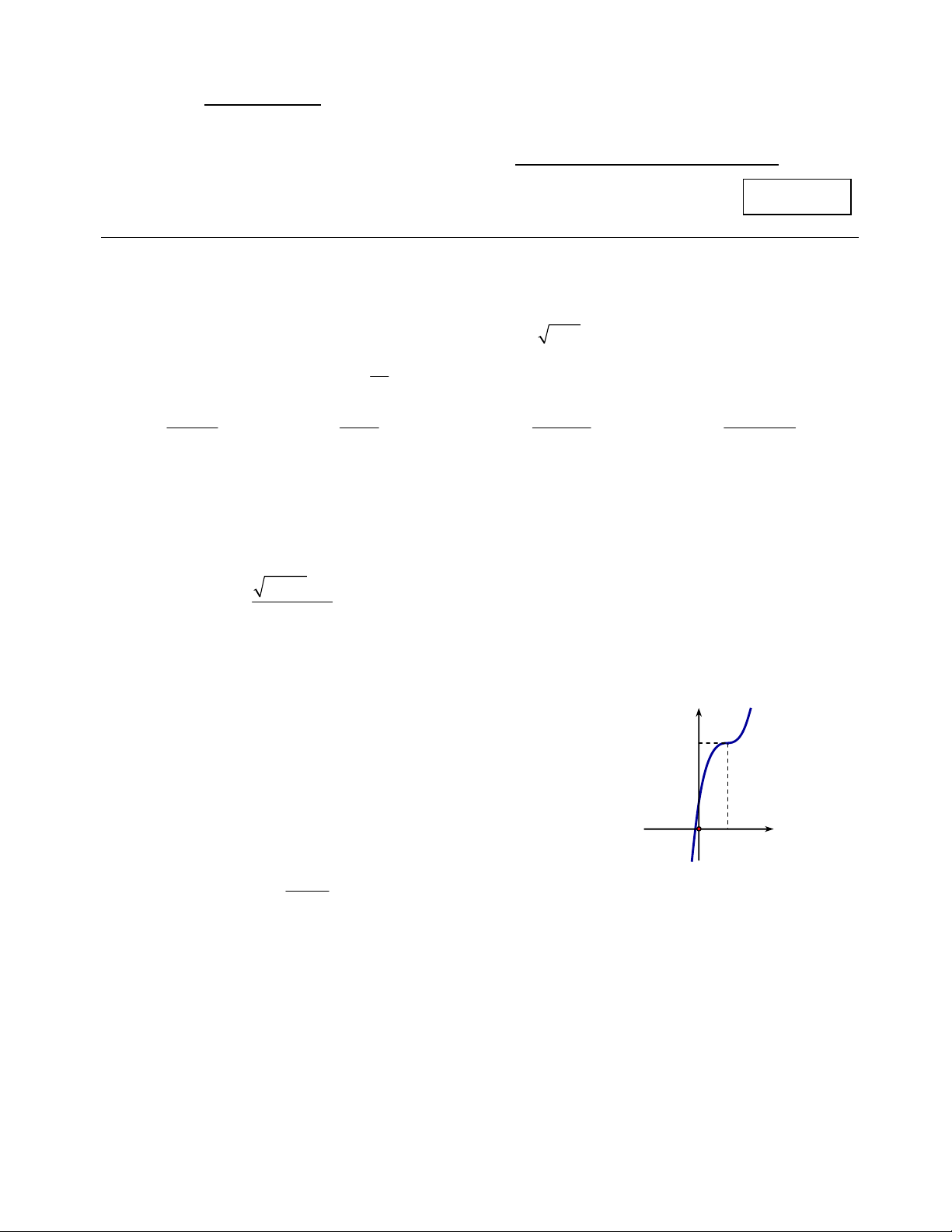
Câu 7: Đường cong ở hình bên là đồ thị của một trong bốn hàm
số ở dưới đây. Hàm số đó là hàm số nào?
A. 32
261.yxx x
B. 32
2661.yx x x
C. 32
2661.yx x x
D. 32
2661.yxxx O
x
y
1
3
Câu 8: Đồ thị hàm số 23
1
x
yx
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A. 1
x
và 2y. B. 2x và 1y
. C. 1
x
và 3y
. D. 1x và 2y
.
Câu 9: Có 7 bông hồng đỏ, 8 bông hồng vàng và 10 bông hồng trắng, các bông hồng khác nhau từng đôi
một. Hỏi có bao nhiêu cách lấy 3 bông hồng có đủ ba màu.
A. 319 B. 3014 C. 310 D. 560
Câu 10: Giá trị của m làm cho phương trình
2
22 30
mxmxm có 2 nghiệm dương phân biệt là
A. 6m. B. 6
m và 2
m.
C. 26m hoặc 3m. D. 0
m hoặc 26
m.
Câu 11: Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Mã đề 101
Trang 2/6 – Mã đề 101
B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với
đường thẳng còn lại.
C. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
D. Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một
đường thẳng thì song song với nhau.
Câu 12: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt phẳng (ABC),
A
H là đường cao trong tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
A
HAC. B.
A
HBC . C. SA BC
. D.
A
HSC.
Câu 13: Cho hàm số
32
32
3
x
yx có đồ thị là
C. Viết phương trình tiếp tuyến với đồ thị
C biết
tiếp tuyến có hệ số góc 9k .
A.

16 9 3yx . B.
93yx . C.
16 9 3yx
 . D.
16 9 3yx .
Câu 14: Cho tứ diện SABC có các cạnh , , SA SB SC đôi một vuông góc với nhau. Biết 3SA a, 4SB a
,
5SC a. Tính theo a thể tích V của khối tứ diện .S ABC .
A. 3
20Va. B. 3
10Va. C.
3
5
2
a
V. D. 3
5Va.
Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Tứ diện có bốn cạnh bằng nhau là tứ diện đều
B. Hình chóp tam giác đều là tứ diện đều
C. Tứ diện có bốn mặt là bốn tam giác đều là tứ diện đều
D. Tứ diện có đáy là tam giác đều là tứ diện đều
Câu 16: Hàm số 2sin 1
1cos
x
y
x
xác định khi
A. 2
2
x
k
 B.
x
k
C. 2
x
k
D. 2
x
k

Câu 17: Cho hàm số ()yfxđồng biến trên khoảng (;)ab . Mệnh đề nào sau đây sai?
A. Hàm số (1)yfx
đồng biến trên khoảng (;)ab
B. Hàm số () 1yfx nghịch biến trên khoảng (;)ab
C. Hàm số () 1yfx
đồng biến trên khoảng (;)ab
D. Hàm số () 1yfx nghịch biến trên khoảng (;)ab
Câu 18: Đạo hàm của hàm số 3
sin 4
2
y
x




là:
A. 4cos4x B. 4cos4
x
C. 4sin4
x
D. 4sin4
x
Câu 19: Phương trình : cos 0xm
vô nghiệm khi m là:
A. 11m B. 1m C. 1m
D. 1
1
m
m

Câu 20: Cho hình chóp .S ABC có ', '
A
B lần lượt là trung điểm của ,.SA SB Gọi 12
,VV lần lượt là thể tích
của khối chóp .''SABC
và ..S ABC Tính tỉ số 1
2
V
V.
A. 1
8 B. 1
4 C. 1
2 D. 1
3
Câu 21: Trong mặt phẳng Oxy cho tam giác ABC có
(
)
(
)
(
)
2;1 , 1; 2 , 3; 0AB C-. Tứ giác ABCE là hình
bình hành khi tọa độ đỉnh E là cặp số nào dưới đây?
Trang 3/6 – Mã đề 101
A.
()
6; 1-. B.
()
0;1 . C.
()
1; 6 . D.
()
6;1 .
Câu 22: Cho đường thẳng :2 1 0.dxy Để phép tịnh tiến theo v
biến đường thẳng d thành chính nó
thì v
phải là véc tơ nào sau đây:
A.
1; 2 .v
B.
2; 1 .v
C.
1; 2 .v
D.

2;1 .v
Câu 23: Hàm số nào sau đây đạt cực tiểu tại 0x
?
A. 32yx B. 21yx C. 31yxx
 D. 32
32yx x
Câu 24: Cho hàm số

= yfx
xác định trên và có đồ thị như
hình vẽ bên. Mệnh đề nào sau đây đúng ?
A. Hàm số đồng biến trên mỗi khoảng
1; 0 và (1;+∞).
B. Hàm số đồng biến trên mỗi khoảng
;1
 và
0;1 .
C. Hàm số nghịch biến trên khoảng

1;1.
D. Hàm số nghịch biến trên mỗi khoảng
1; 0 và (1;+∞).
Câu 25: Cho hình chóp .SABCD có đáy
A
BCD là hình vuông cạnh a, SA vuông góc với mặt đáy
(ABCD), 2SA a. Tính theo a thể tích khối chóp .S ABC .
A.
3
3
a. B.
3
6
a. C.
3
4
a. D.
3
2
5
a.
Câu 26: Cho hàm số
f
xcó đạo hàm trên và có đồ
thị
yf
x
như hình vẽ. Xét hàm số
22gx f x
. Mệnh đề
nào sau đây sai?
A. Hàm số
g
xnghịch biến trên

0; 2 .
B. Hàm số
g
xđồng biến trên
 .
C. Hàm số
g
xnghịch biến trên
 .
D. Hàm số
g
xnghịch biến trên
1; 0.
Câu 27: Tìm tất cả các giá trị của tham số m để hàm số 1mx
y
x
m
đồng biến trên khoảng (2; ) .
A. 21m
hoặc 1m B. 1m
hoặc 1m.
C. 11m . D. 1m
hoặc 1m.
Câu 28: Cho cấp số nhân
n
u có công bội q và 10u. Điều kiện của q để cấp số nhân
n
u có ba số
hạng liên tiếp là độ dài ba cạnh của một tam giác là:
A. 01q
B. 15
12
q
 C. 1q D. 15 15
22
q


Câu 29: Cho tam giác ABC có (1; 1), (3; 3), (6;0).AB C-- Diện tích ABCD là
A. 6. B. 62. C. 12. D. 9.
Câu 30: Tính tổng 0 1 2 2000
2000 2000 2000 2000
2 3 ... 2001CCC C
A. 2000
1000.2 B. 2000
2001.2 C. 2000
2000.2 D. 2000
1001.2
Trang 4/6 – Mã đề 101
Câu 31: Cho hàm số 42
yax bx c có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. 0,a0,b0c
B. 0,a0,b0c
C. 0,a0,b0c
D. 0,a0,b0c
Câu 32: Gọi S là tập các giá trị dương của tham số m sao cho hàm số 32
3. 27 3 2yx mx x m
 đạtcực
trị tại 12
,
x
x thỏa mãn 12
5xx
. Biết
;Sab. Tính 2Tba
.
A. 51 6T. B. 61 3T. C. 61 3T
. D. 51 6T.
Câu 33: Cho hình hộp .'' ' '
A
BCD A B C D có tất cả các mặt là hình vuông cạnh a. Các điểm ,
M
N lần lượt
nằm trên ',
A
DDB
sao cho
A
MDNx
(02
x
a ). Khi
x
thay đổi, đường thẳng
M
N luôn song
song với mặt phẳng cố định nào sau đây?
A.
''CB D B.
'
A
BC C.
'
A
DC D.
''BA C
Câu 34: Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp đó. Gọi P
là xác suất để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng:
A. 1
12 B. 16
33 C. 10
33 D. 2
11
Câu 35: Cho đồ thị 21
(): 1
x
Cy x
. Gọi
M
là điểm bất kì thuộc đồ thị ()C. Tiếp tuyến của đồ thị ()Ctại
M
cắt hai đường tiệm cận của ()Ctại hai điểm Pvà .Q Gọi G là trọng tâm tam giác IPQ (với Ilà giao
điểm hai đường tiệm cận của ()C). Diện tích tam giác GPQ là
A. 2. B. 4. C. 2.
3 D. 1.
Câu 36: Cho khối hộp .
A
BCDABCD

có thể tích bằng 2018. Gọi
M
là trung điểm của cạnh
A
B. Mặt
phẳng ()
M
BD

chia khối hộp .
A
BCD A B C D

thành hai khối đa diện. Tính thể tích của phần khối đa diện
chứa đỉnh A.
A. 5045
6. B. 7063
6. C. 10090
17 . D. 7063
12 .
Câu 37: Cho lăng trụ tam giác .'' '
A
BC A B C . Đặt 'AA a
 , AB b

, AC c
 , Gọi
I
là điểm thuộc đường
thẳng 'CC sao cho 1
''
3
CI CC
  , G điểm thỏa mãn 0


   
GB GA GB GC . Biểu diễn vectơ IG
 qua các
vectơ ,,abc

. Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
A. 11 23
43
IG a b c




 B.
12
3
I
Gabc
 .
C.
12
4
I
Gacb
 . D. 11
2
43
IG b c a




 .
Câu 38: Cho hình chóp S.ABC có 1, 2, 3SA SB SC
và
000
60 , 120 , 90ASB BSC CSA
. Tính thể tích
khối chóp .SABC
.
A. 2
2. B. 2. C. 2
6. D. 2
4.
Câu 39: Trong hệ tọa độ Oxy , cho tam giác
A
BC có phương trình đường thẳng : 7 13 0.BC x y
Các
Trang 5/6 – Mã đề 101
chân đường cao kẻ từ ,BC lần lượt là (2;5), (0;4).EF Biết tọa độ đỉnh
A
là (;).
A
ab Khi đó:
A. 5ab B. 26ab C. 26ab
D. 5ba
Câu 40: Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2
4
31 12 1xmx x
 có
hai nghiệm thực?
A. 11
3m
. B. 1
23
m . C. 1
14
m
. D. 1
03
m
.
Câu 41: Nghiệm của phương trình 0
2
3
4
3sin
4
cossincos 44
xxxx là:
A. Zkkx ,
3
B. Zkkx ,2
3
C. Zkkx ,2
4
D. Zkkx ,
4
Câu 42: Cho dãy số
n
u xác định bởi: 22 2
13 21
...
n
n
unn n
 với *
n. Giá trị của lim n
u bằng:
A. 0 B.  C.
D. 1
Câu 43: Cho hình chóp .SABCD
đáy là hình thang vuông tại A và
B
, ,2.
A
BBCaAD a

Biết SA
vuông góc với đáy (ABCD), .SA a Gọi ,
M
N lần lượt là trung điểm ,SB CD . Tính sin góc giữa đường
thẳng
M
N và mặt phẳng
SAC .
A. 5
5 B. 55
10 C. 35
10 D. 25
5.
Câu 44: Cho hai số thực ,
x
y thay đổi thỏa mãn điều kiện 22
2xy
. Gọi M,mlần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của biểu thức 33
2( ) 3
P
xy xy. Giá trị của của
M
m
bằng
A. 4 B. 1
2
C. 6
D. 142
Câu 45: Đường dây điện 110KV kéo từ trạm phát (điểm A) trong đất liền ra đảo (điểm C). Biết khoảng
cách ngắn nhất từ C đến B là 60km, khoảng cách từ A đến B là 100km, mỗi km dây điện dưới nước chi phí
là 100 triệu đồng, chi phí mỗi km dây điện trên bờ là 60 triệu đồng. Hỏi điểm G cách A bao nhiêu km để
mắc dây điện từ A đến G rồi từ G đến C chi phí thấp nhất? (Đoạn AB ở trên bờ, đoạn GC dưới nước)
A. 50 (km)
B. 60 (km)
C. 55 (km)
D. 45 (km)
Câu 46: Tập hợp các giá trị của tham số m để hàm số 43 2
3412 1yx x xm
 có 7 điểm cực trị là
A. (0;6) B. (6;33) C. (1; 33) D. (1; 6)
Câu 47: Tính tổng tất cả các nghiệm của phương trình
x
xx
xx 2
32
2
cos
1coscos
tan2cos
trên đoạn

70;1
A. 188
B. 263
C. 363
D. 365
Câu 48: Cho hàm số 32
25yx x x
có đồ thị
C. Trong các tiếp tuyến của
C, tiếp tuyến có hệ số
góc nhỏ nhất, thì hệ số góc của tiếp tuyến đó là
A. 4
3. B. 5
3. C. 2
3. D. 1
3.