Trang1/9–Mãđề001‐https://toanmath.com/
SỞGIÁODỤCVÀĐÀOTẠO
TỈNHĐIỆNBIÊN
KỲTHITHỬTHPTQUỐCGIA
NĂMHỌC2018‐2019
MÔN:TOÁN
Thờigianlàmbài:90Phút;(Đềthicó50câu)
(Đềthicó09trang)
Họvàtênthísinh:…………………………….Sốbáodanh:………………
ĐỀBÀI
Câu1: Thểtíchkhốihộpchữnhậtcóbakíchthướclầnlượt,2 ,3aaabằng
A.3
2a.B.3
8a.C.3
4a.D.3
6a
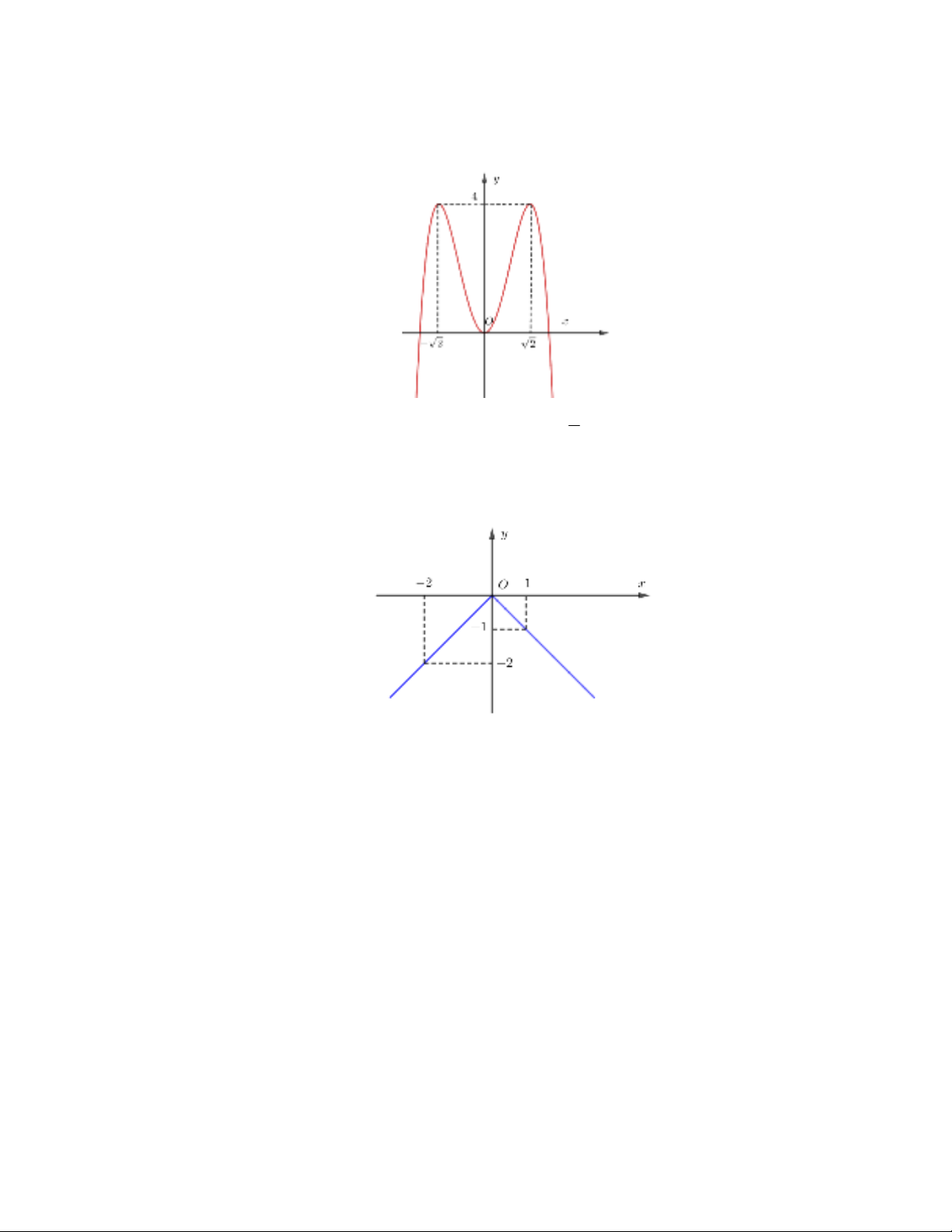
Câu2: Chohàmsố

yfx
cóbảngbiếnthiênnhưsau:
Mệnhđềnàodướiđâyđúng?
A.Hàmsốđồngbiếntrênkhoảng

;1 .
B.Điểmcựcđạicủađồthịhàmsốlà 1x.
C.Hàmsốnghịchbiếntrênkhoảng
1; 3 .
D.Giátrịcựctiểucủahàmsốlà1.
Câu3: TrongkhônggianOxyz ,cho
1;1; 3A,
3; 1;1B.GọiGlàtrọngtâmtamgiácOAB
,véctơ

OG cóđộdàibằng:
A.25
3.B.25
5.C.35
3.D.35
2.
Câu4: Chohàmsố ()yfx
cóđồthịlàđườngcongtronghìnhvẽbên.Hàmsố ()fxđạtcực
đạitạiđiểmnàosauđây?
A.1x.B.2x.C.1x.D.2x.
Mãđề001
ĐỀTHITHỬ
Trang2/9–Mãđề001‐https://toanmath.com/
Câu5: Vớicácsốthựcdương,ab
bấtkì.Mệnhđềnàodướiđâyđúng?
A.log( ) log .logab a b .B.log
log log
a
a
bb
.
C.log( ) log logab a b .D.log log log
aba
b.
Câu6: Cho

5
1
6fxdx và

5
1
8gxdx .Giátrịcủa:
 


5
1
4fx gx dx
bằng:
A.16.B.14.C.12.D.10.
Câu7: Chokhốitrụcóthiếtdiệnquatrụclàhìnhvuôngcạnha.Thểtíchkhốitrụlà:
A.
3
.
4
a.B.
3
.
3
a.C.
3
.
12
a.D.
3
a.
Câu8: Giảibấtphươngtrình

1
2
log 3 1 0x.
A.1
2
x.B.2
3
x.C.2
3
x.D.
12
33
x.
Câu9: TrongkhônggianOxyz ,viếtphươngtrìnhđoạnchắnmặtphẳngđiquađiểm
 
2,0,0 ; 0, 3,0 ; 0,0,2AB C
A.1
232
y
xz
.B.
1
232
y
xz
.C.
1
322
y
xz
.D.
1
223
y
xz
.
Câu10: Chohàmsố

fx
liêntụctrênvà

d
6
0
10fx x ,thì

d
3
0
2fxxbằng:
A.30.B.20.C.10.D.5.
Câu11: TrongkhônggianOxyz ,đườngthẳng



2
3
2
xt
yt
zt
điquađiểmnàosauđây:
A.

1; 2; 1A.B.
3;2; 1A.C.
3; 2; 1A.D.
3; 2;1A.
Câu12: Chon vàklàhaisố nguyêndươngtùyýthỏamãnknmệnhđềnàodướiđây
đúng
A.
!
!( )!
k
n
n
Akn k . B.


1
11 (1 )
kk k
nn n
CCC kn.
C.
1(1 )
kk
nn
CC kn
. D.
!
()!
k
n
n
Cnk.
Câu13: Chocấpsốnhân
n
ucó

1
1
3, 2
uq khiđó3
256 làsốhạngthứmấy?
A.thứ8.B.thứ9.C.thứ7.D.thứ6.
Câu14: Điểmnàobiểudiễnsốphứcliênhợpcủasốphức23zilà
Trang3/9–Mãđề001‐https://toanmath.com/
A.
2; 3M.B.
2;3M.C.
2;3M.D.
2; 3M.
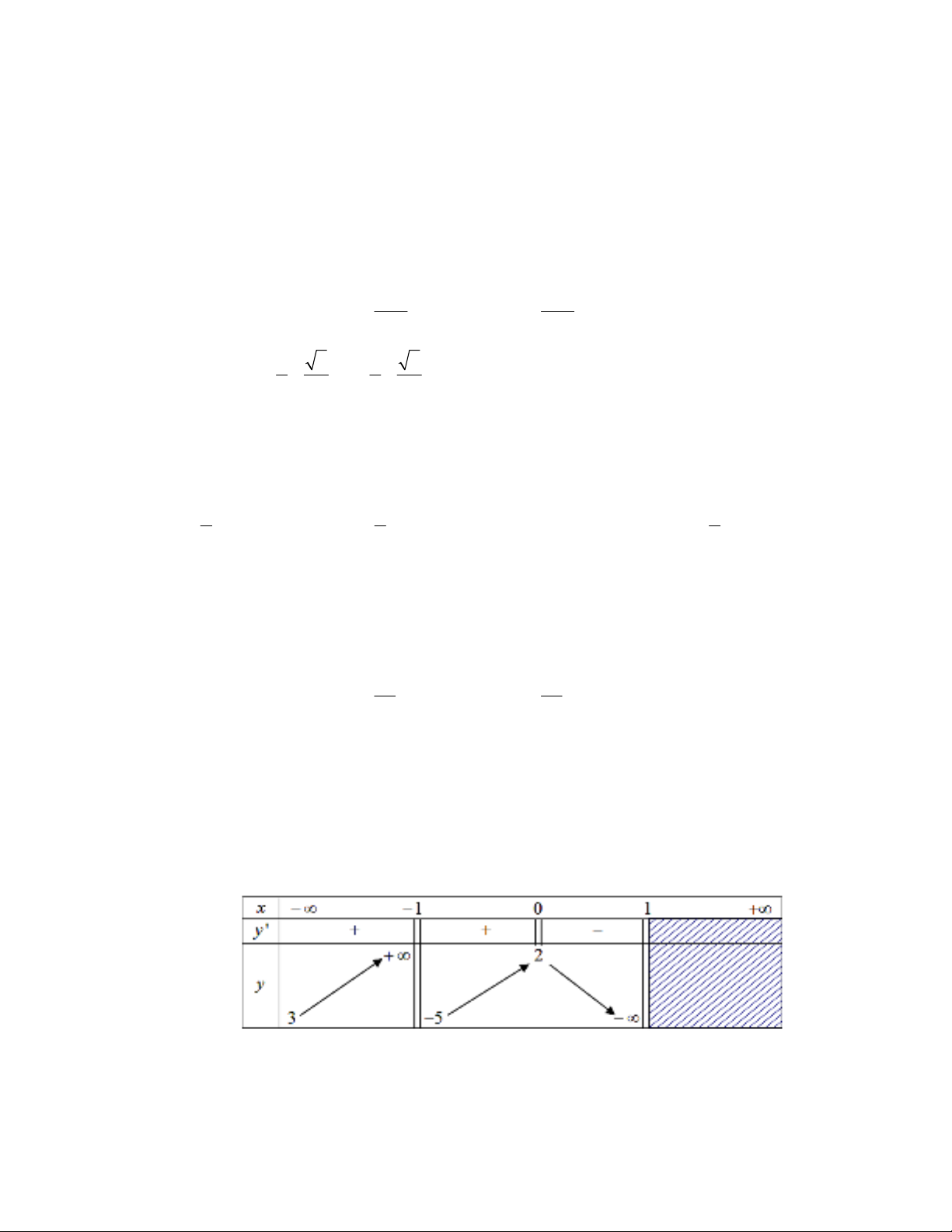
Câu15: Đườngcongtronghìnhvẽbênlàđồthịhàmsốnàodướiđây
A.
42
2yx x
.B.
42
4yx x
.C.
42
12
4
yxx
.D.
42
3yx x
.
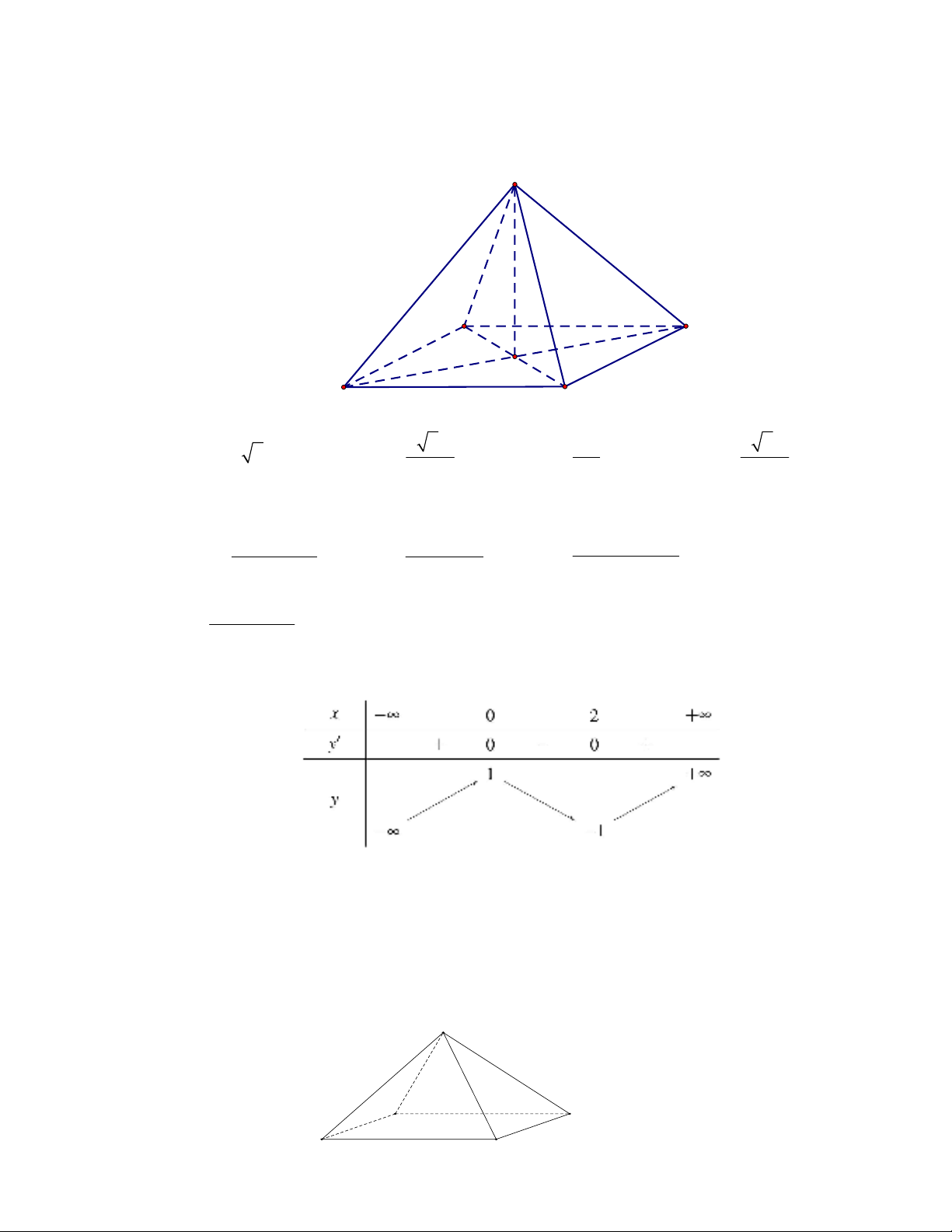
Câu16: Hàmsố ()yfx
cóđồthịnhưhìnhvẽ
Mệnhđềnàosauđâyđúng?
A.Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố

yfx
trênđoạn

2;1 lầnlượt
là
0fvà
2f.
B.Giátrị nhỏ nhất,giátrị lớnnhấtcủahàmsố

f
xtrênđoạn

2;1 lầnlượtlà
2f

1
f
.
C.Hàmsốkhôngcócựctrị.
D.Hàmsốnhậngiátrịâmvớimọix.
Câu17: Chohàmsố

yfx
có


3
213 5fx xx xx .Sốcựctiểucủađồthịhàmsố
là
A.4.B.1.C.2.D.3.
Câu18: Chosố phứczthỏamãnphươngtrình
2
(3 2 ) (2 ) 4iz i i.TọađộđiểmMbiểu
diễnsốphứczlà
Trang4/9–Mãđề001‐https://toanmath.com/
A.

1;1M
.B.

1; 1M
.C.

1;1M
.D.

1; 1M
.
Câu19: Trongkhônggian
Oxyz
,chohaiđiểm

1;1; 0A
và

1; 3; 2B
.Phươngtrìnhcủamặt
cầuđườngkínhABlà
A.


222
1102xyz
.B.


222
1212xyz
.
C.


222
1325xyz
.D.


222
1322xyz
.
Câu20: Cho
log log
23
5; 5ab
.Khiđó
5
log 6
tínhtheoavàblà:
A.
.ab
B.
.
ab
ab
C.
.
ab
ab
D.
22
.ab
Câu21: Haisốphức
37
22
ivà
37
22
ilànghiệmcủaphươngtrìnhnàosauđây?
A.

2
340zz
.B.

2
340zz
.C.

2
340zz
.D.

2
340zz
.
Câu22: Trongkhônggianvớihệ trụctọađộ khoảngcáchtừ tâmmặtcầu

222
44410xyz xyz
đếnmặtphẳng(P)
22100xyz
bằng
A.
4
3
.B.
7
3
.C.0.D.
8
3
.
Câu23: Tìmtậpnghiệm
S
củabấtphươngtrình


2
ln ln 4 4 .xx
A.

2;S
.B.

1;S
.C.

\2S
.D.

1; \ 2 .S
Câu24: Chokhốinóncóchiềucao
ha
độdàiđườngsinh
2la
Thểtíchkhốinónlà:
A.
3
.a
.B.
3
3
a.C.
3
2
a.D.
3
2.a
.
Câu25: GọiSlàdiệntíchhìnhphẳnggiớihạnbởicácđường
;0, 0, 2
x
yey x x
.Mệnhđề
nàodướiđâyđúng?
A.
22
0
x
Sedx
.B.
2
0
x
Sedx
.C.
22
0
x
Sedx
.D.
2
0
x
Sedx
.
Câu26: Chohàmsố

yfx
cóbảngbiếnthiênnhưhìnhvẽdướiđây
Tổngsốđườngtiệmcậnngangvàtiệmcậnđứngcủađồthịhàmsốđãcholà
A.
1
.B.
2
.C.
0
.D.
3
.
Oxyz
Trang5/9–Mãđề001‐https://toanmath.com/
Câu27: Chohìnhchóptứ giácđều.SABCDcócạnhđáybằng2a,cạnhbênbằng3a(tham
khảohìnhvẽ).TínhthểtíchVcủakhốichópđãcho.
A.3
47Va
.B.3
47
9
a
V.C.3
4
3
a
V.D.3
47
3
a
V.
Câu28: Tínhđạohàmcủahàmsố
43
43ln xyx .
A.
43
1
43
yxx .B.
32
1
412
yxx
.C.


32
2
43
412
43
xx
y
xx
.D.

32
43
412
43
xx
yxx .
Câu29: Chohàmsố ()yfx
cóbảngbiếnthiênnhưhìnhsau
Sốnghiệmthựcdươngcủaphươngtrình2() 2 0fx là
A.0.B.1.C.2.D.3.
Câu30: Chohìnhchóp.SABCDcóđáyABCD làhìnhchữ nhật,3AB ,4BC .Tamgiác
SAC nằmtrongmặtphẳngvuônggócvớiđáy,khoảngcáchtừđiểmCđếnđường
thẳngSA bằng4.Côsincủagócgiữahaimặtphẳng
SAB và
SAC bằng
O
C
S
D
C
A
D
B
S