1
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
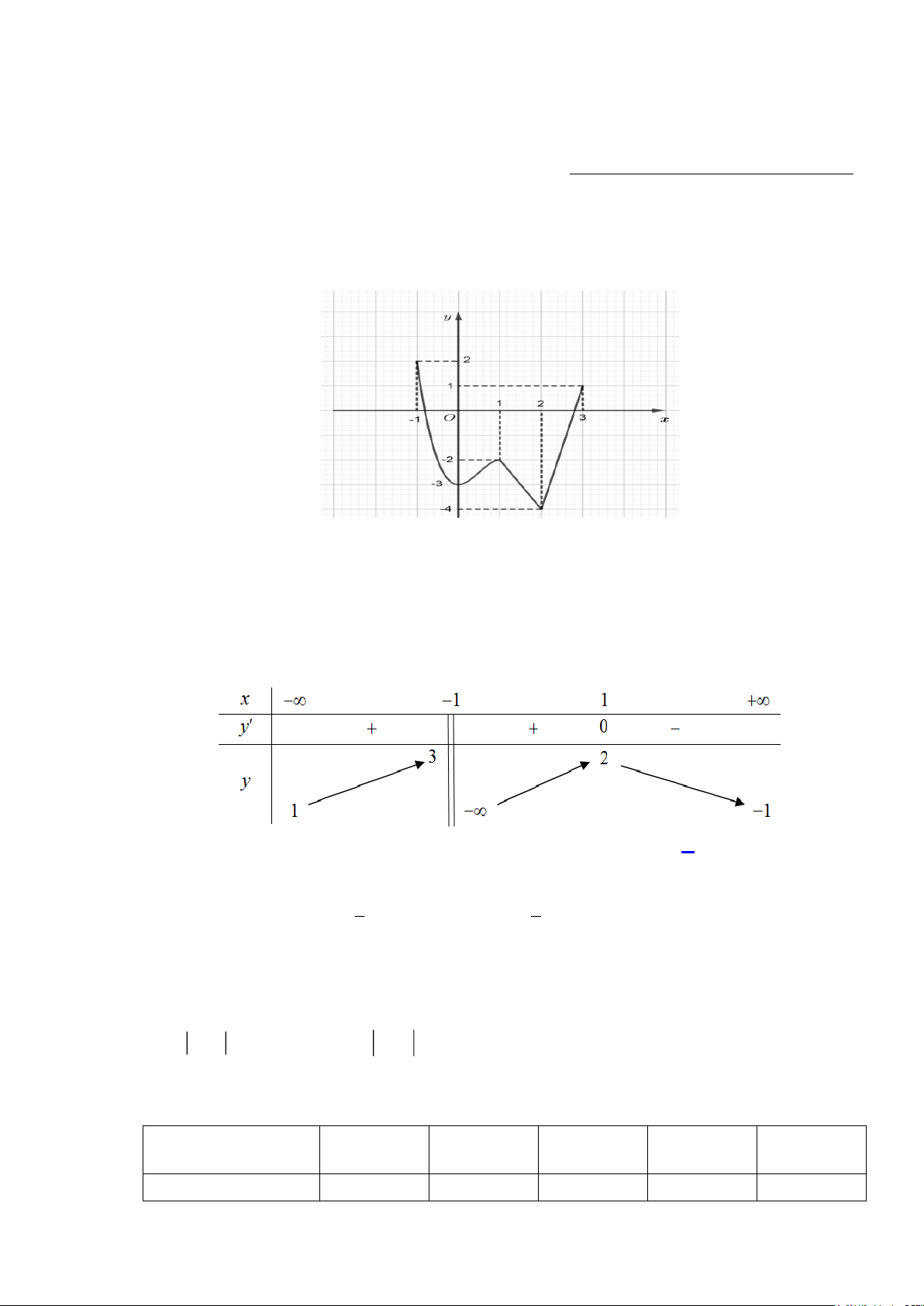
Câu 1: (B-TD) Cho hàm số
()y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ bên.
Gọi
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
. Giá trị
của
Mm
là
A.
2.
B.
6.
C.
5.
D.
2.
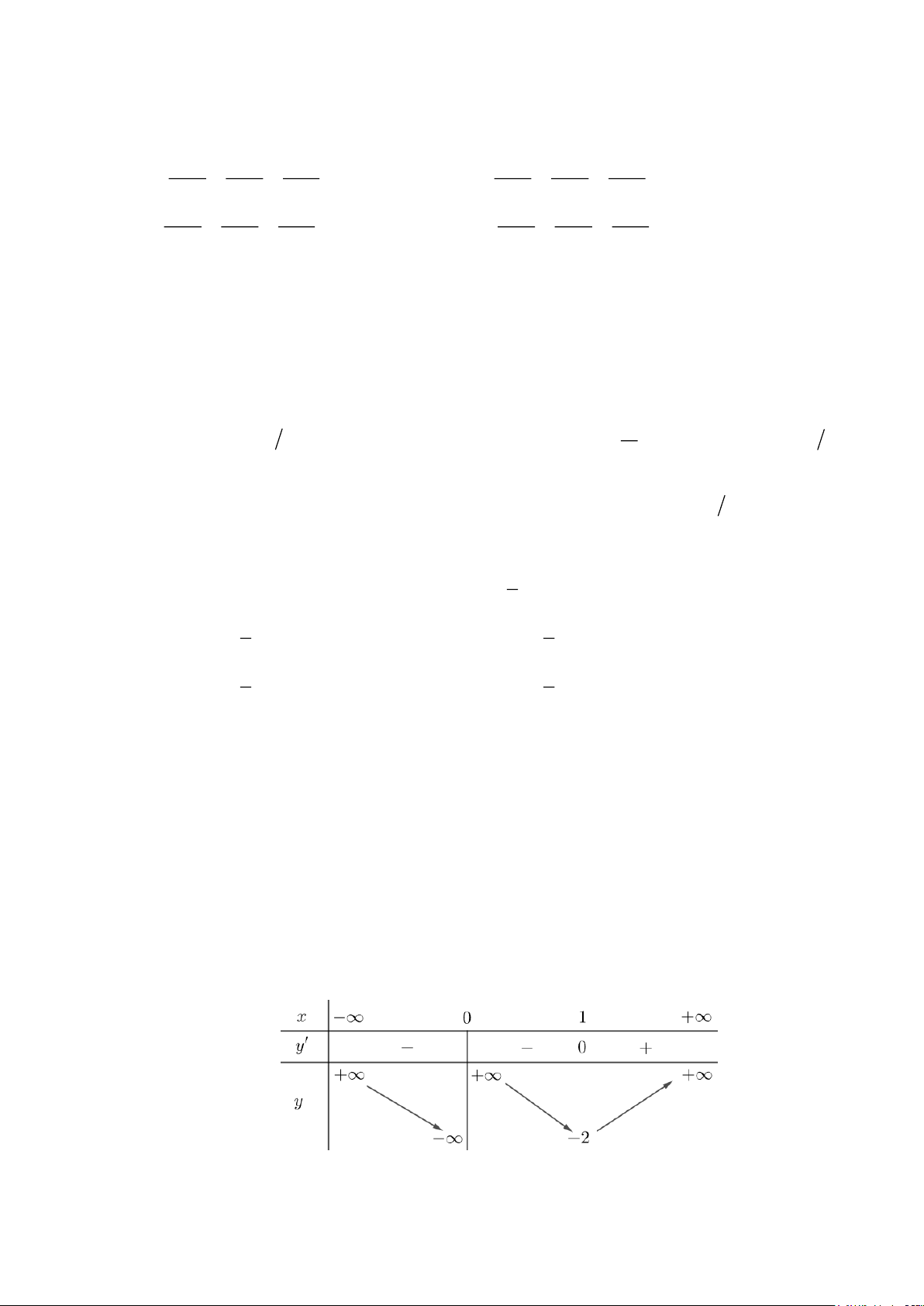
Câu 2: (B-TD) Cho hàm số
có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và
ngang của đồ thị hàm số
?
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 3: (B-TD) Họ nguyên hàm của hàm số
3
(x) x
fe
là hàm số nào sau đây?
A.
3x
eC
. B.
3
1
3x
eC
. C.
1
3x
eC
. D.
3
3x
eC
.
Câu 4: (H-TD) Cho hàm số
( )
y f x=
liên tục trên đoạn
[ ]
;ab
Hình phẳng
( )
H
giới hạn bởi đồ thị hàm số
( )
y f x=
, trục hoành và hai đường thẳng
xa=
;
xb=
Hình phẳng
( )
H
có diện tích bằng
A.
( ) d
a
b
f x x
ò
. B.
( )
d
b
a
f x x
ò
. C.
f(x)d
b
a
x
ò
. D.
( )
2d
b
a
V f x xpéù
=ëû
ò
.
Câu 5: (H-TD) Bạn A sử dụng tính năng ghi lại số phút sử dụng điện thoại của mình mỗi ngày trong một
tháng. Kết quả được ghi lại ở bảng sau:
Số bước (đơn vị:
phút)
[60; 65)
[65; 70)
[70; 75)
[75; 80)
[80; 85)
Số ngày
6
7
6
6
5
Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng
TRƯỜNG THPT SỐ 1 NGHĨA HÀNH
ĐỀ THI THỬ - TN THPT 2025
Bài thi môn: TOÁN
(Đề gồm có 04 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
2
A.
25
. B.
2
. C.
75
. D.
0
.
Câu 6: (B-TD) Trong không gian với hệ toạ độ
Oxyz
, phương trình đường thẳng đi qua hai điểm
2;3;2A
và
5;4; 1B
là
A.
2 3 2
7 1 3
x y z

. B.
2 3 2
7 1 3
x y z

.
C.
2 3 2
5 4 1
x y z

. D.
2 3 2
5 4 1
x y z

.
Câu 7: (B-TD) Trong không gian với hệ toạ độ
Oxyz
, mặt cầu
22
2
: 1 3 16S x y z
có tâm là
A.
1;0;3I
. B.
1;0;3I
. C.
1;0; 3I
. D.
1;2; 3I
.
Câu 8: (B-TD) Cho
a
và
b
là hai số thực dương thỏa mãn
32 16ab
. Giá trị của
22
3log 2logab
bằng
A.
4
. B.
5
. C.
2
. D.
32
.
Câu 9: (H-TD) Mức cường độ âm L đo bằng decibel (dB) của âm thanh có cường độ I (đo bằng mét
vuông, kí hiệu
2
Wm
) được định nghĩa như sau:
0
10log I
LI I
, trong đó
12 2
010I W m
là cường độ âm thanh nhỏ nhất mà tai người có thể phát hiện được (gọi là ngưỡng nghe).
Mức cường độ âm của cuộc trò chuyện bình thường có cường độ
72
10I W m
là
A.
50 dB
. B.
170 dB
. C.
20 dB
. D.
80 dB
.
Câu 10: (H-TD) Cho cấp số cộng
n
u
có
13u
và
1.
2
d
Khẳng định nào sau đây đúng?
A.
1
3 1 .
2
n
un
B.
1
3 1.
2
n
un
C.
1
3 1 .
2
n
un
D.
1
3 1 .
4
n
un
Câu 11: (B-TD) Cho hình chóp
.S ABC
có
SC
vuông góc
ABC
. Góc giữa
SA
với
ABC
là góc
giữa:
A.
SA
và
AB
. B.
SA
và
SC
. C.
SB
và
BC
. D.
SA
và
AC
.
Câu 12: (B-TD) Trong không gian
Oxyz
, cho điểm
1;2; 3A
. Hình chiếu vuông góc của
A
lên mặt
phẳng
Oxy
có tọa độ là
A.
0;2; 3
. B.
1;0; 3
. C.
1;2;0
. D.
1;0;0
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số
y f x
có bảng biến thiên như hình vẽ. Phát biểu nào sau đây là đúng.
Các mệnh đề sau đúng hay sai?
a)(B-TD) Hàm số đạt cực tiểu tại
2x
.
b) (H-TD)
0;3 2Min y 
.
3
c)(H-TD) Đồ thị hàm số có một đường tiệm cận ngang.
d) (H-TD) Hàm số nghịch biến trên khoảng
;
.
Câu 2: Hàm chi phí cận biên của sản phẩm được định nghĩa là đạo hàm của hàm chi phí. Một nhà máy
sản xuất X với số lượng
x
sản phẩm A thì chi phí cận biên được mô hình hóa bởi công thức
2
6 10 15f x x x
(nghìn đồng) và chi phí sản xuất một sản phẩm A là 52 nghìn đồng. Các
mệnh đề sau đúng hay sai?
a) (B-TD) Nếu hàm chi phí sản phẩm A là
()Fx
thì
( ) ( )F x f x
.
b) (B-TD)
( ) ( ) ( )
b
a
F b F a f x dx
.
c) (H-TD)
(1) 52F
.
d) (VD-MHH) Chi phí sản xuất 10 sản phẩm là
2100
(nghìn).
Câu 3: Lớp 10A có 35 học sinh, mỗi học sinh đều giỏi ít nhất một trong hai môn Toán hoặc Văn. Biết
rằng có 23 học sinh giỏi môn Toán và 20 học sinh giỏi môn Văn. Chọn ngẫu nhiên một học sinh
của lớp 10A.
a) (H-TD) Xác suất để học sinh được chọn giỏi môn Toán biết rằng học sinh đó cũng giỏi môn
Văn bằng
2
5
.
b) (H-TD) Xác suất để học sinh được chọn "giỏi môn Văn biết rằng học sinh đó cũng giỏi môn
Toán" bằng
8
23
.
c) (H-TD) Xác suất để học sinh được chọn "không giỏi môn Toán biết rằng học sinh đó giỏi môn
Văn" bằng
15
23
.
d) (VD-GQVĐ) Xác suất để học sinh được chọn "không giỏi môn Văn biết rằng học sinh đó giỏi
môn Toán" bằng
3
5
.
Câu 4: Trong không gian
Oxyz
, Hai máy bay cùng xuất phát từ hai phi trường, trên màn hình rađa của
trạm điều khiển (với đơn vị trên ba trục chính theo đơn vị km), sau khi xuất phát
t
giờ
0t
, vị
trí của máy bay số một được xác định bởi công thức
20 2
20
10
xt
yt
zt


, vị trí máy bay số hai có tọa độ
là
30 20 10;;t t t
a)(H-MHH) Côsin góc giữa hai máy bay số một và máy bay số hai là
52
6
.
b) (H-MHH) Sau
10
giờ kể từ thời điểm bay hai máy bay gần nhau nhất
c) (H-MHH) Nếu máy bay số một vẫn ở phi trường (đứng ở vị trí ban đầu) thì vị trí tọa độ của máy
bay là
20 20 10;;
d) (VD-MHH) Sau
5
giờ thì vị trí tọa dộ máy bay số 2 trong không gian là
35 25 10;;
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
4
Câu 1:(VD-MHH) Cây cà chua khi trồng có chiều cao
5cm
. Tốc độ tăng chiều cao của cây cà chua sau
khi trồng được cho bởi hàm số:
32
01 ,v t t t
, trong đó
t
tính theo tuần,
vt
tính bằng
centimét/tuần. Gọi
ht
là độ cao của cây cà chua ở tuần thứ
t
. Chiều cao cây cà chua sau
2
tuần là bao nhiêu? Làm tròn kết quả đến số thập phân thứ 2
Câu 2: (VD-GQVD) Trong không gian
Oxyz
cho hai đường thẳng
12
411
55
42 4 2
62
: ; :
xt y
xz
d y t d
zt



. Đường thẳng
d
đi qua
5 3 5;;A
cắt
12
,dd
lần lượt
ở
,BC
. Tính tỉ số
AB
AC
Câu 3: (VD-MHH) Một chiếc hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng;
các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có 60% số
viên bi màu đỏ đánh số và 50% số viên bi màu vàng có đánh số, những viên bi còn lại không
đánh số.
Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số là bao
nhiêu? (kết quả là tròn đến hàng phần trăm)
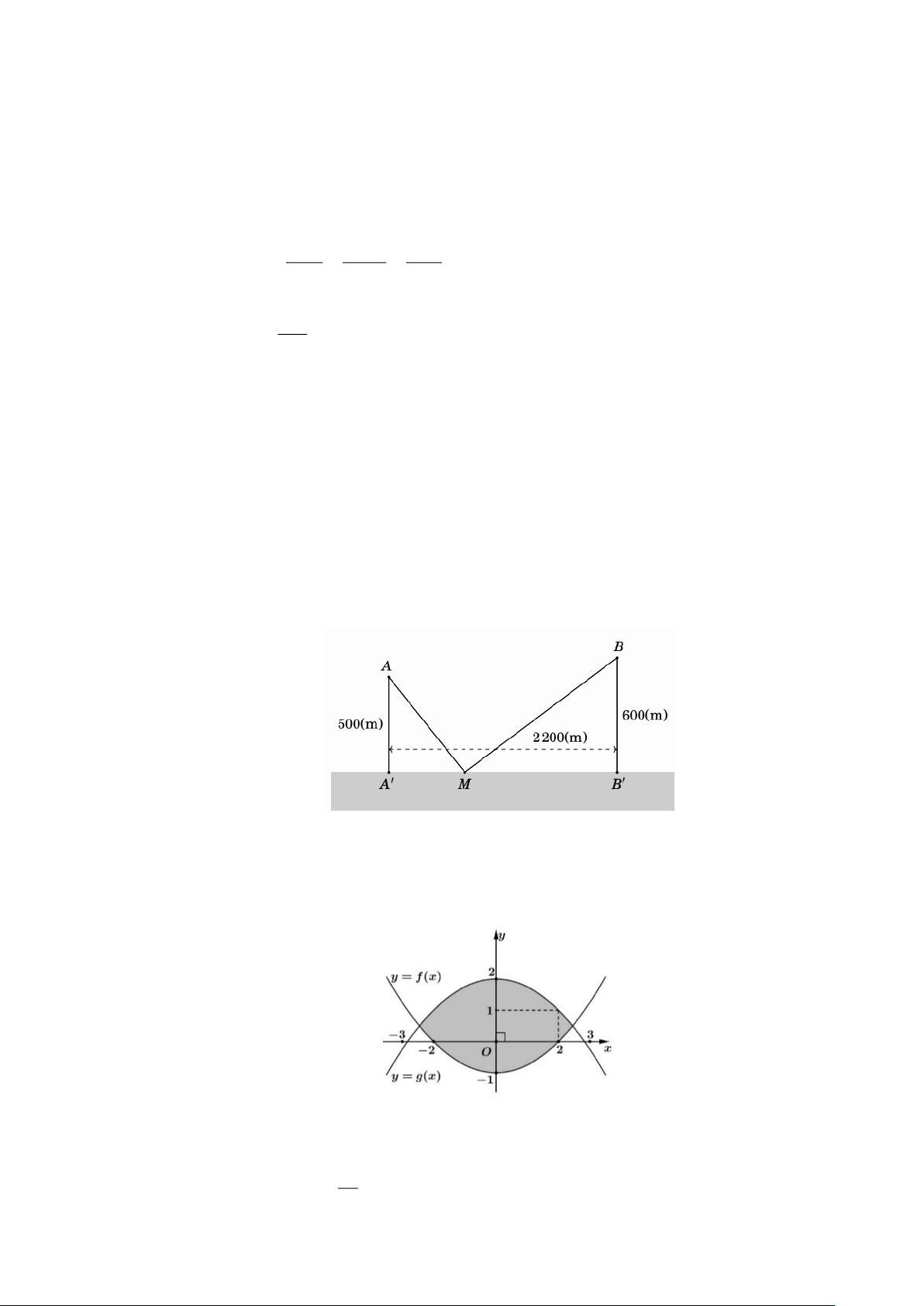
Câu 4: (VD-MHH) Có hai xã
,AB
cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần
lượt là
550AA
m,
600BB
m. Người ta đo được
2200AB

m như hình vẽ dưới đây. Các
kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm cạnh bên bờ sông cho người dân của
hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí
M
của trạm cung cấp nước
sạch đó trên đoạn
AB

sao cho tổng khoảng cách từ hai xã đến vị trí
M
là nhỏ nhất. Hãy tìm
giá trị nhỏ nhất của tổng khoảng cách đó.
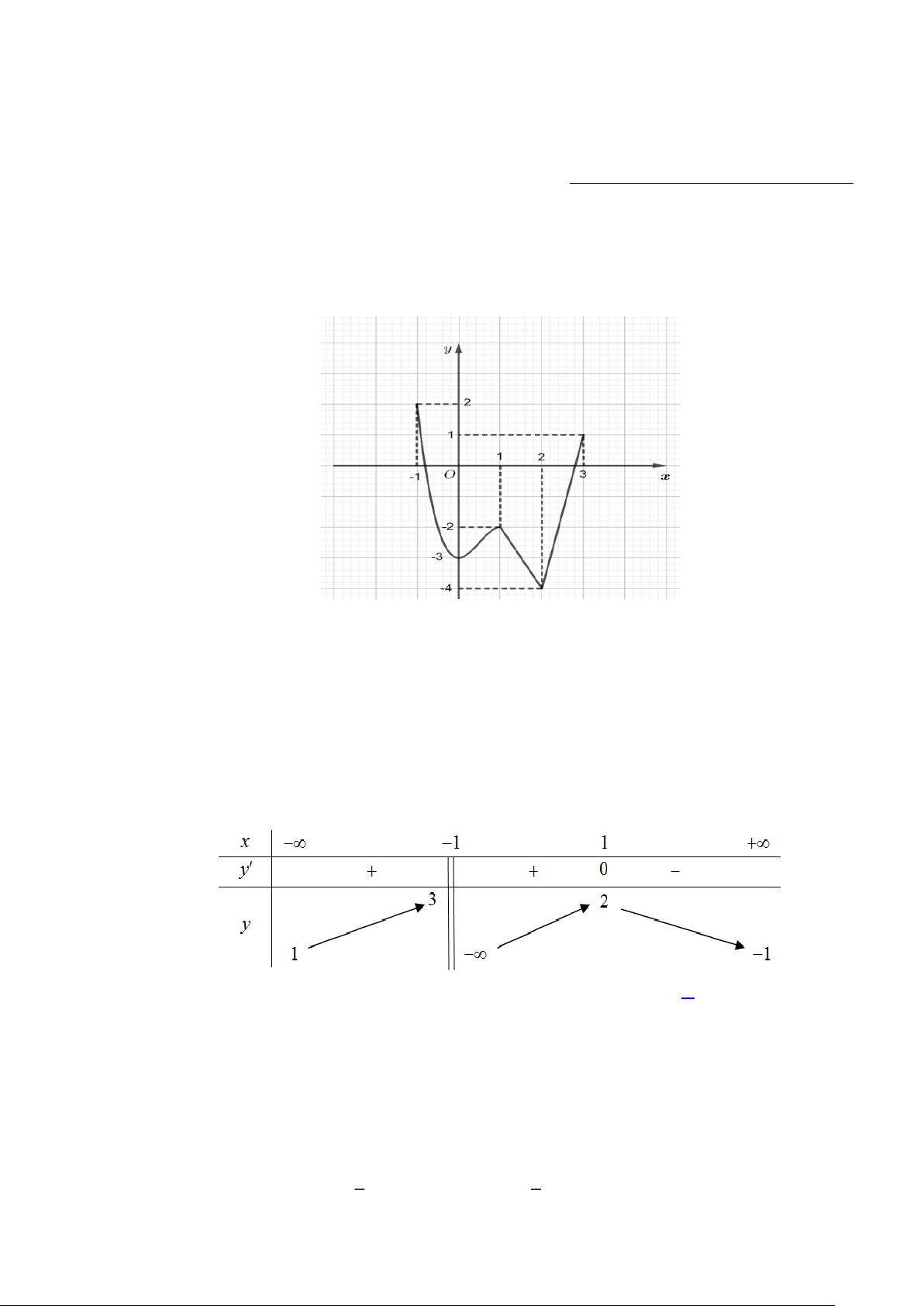
Câu 5: (VD-MHH) Bạn Hải nhận thiết kế logo hình con mắt (phần được tô đậm) cho một cơ sở y tế:
Logo là hình phẳng giới hạn bởi hai parabol
y f x
và
y g x
như Hình 7 (đơn vị trên
mỗi trục toạ độ là decimét). Bạn Hải cần tính diện tích của logo để báo giá cho cơ sở y tế đó
trước khi kí hợp đồng. Diện tích của logo là bao nhiêu decimét vuông (làm tròn kết quả đến
hàng phần mười).
Hình 6
Câu 6: (VD-TD) Một hình chóp cụt đều
ABC A BC
có cạnh đáy lớn bằng
4a
, cạnh đáy nhỏ bằng
2a
và chiều cao của nó bằng
3
2
a
. Tìm thể tích của khối chóp cụt đều trên.
5
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: (B-TD) Cho hàm số
()y f x
liên tục trên đoạn
1;3
và có đồ thị như hình vẽ bên.
Gọi
,Mm
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;3
. Giá trị
của
Mm
là
A.
2.
B.
6.
C.
5.
D.
2.
Trả lời:
Từ đồ thị suy ra:
2, 4 2.M m M m
Câu 2: (B-TD) Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và
ngang của đồ thị hàm số
()y f x=
?
A.
0
. B.
1
. C.
2
. D.
3
.
Trả lời:
Nhìn bảng biến thiên ta thấy hàm số có tập xác định
\{1}DR=
,
1
lim , lim 1 lim 1
xxx
y y và y
+
®® - ¥ ® + ¥
= - ¥ = = -
Nên đồ thị hàm số không có 01 tiệm cận đứng và 02 tiệm cận ngang.
Câu 3: (B-TD) Họ nguyên hàm của hàm số
3
(x) x
fe
là hàm số nào sau đây?
A.
3x
eC
. B.
3
1
3x
eC
. C.
1
3x
eC
. D.
3
3x
eC
.
Trả lời:
TRƯỜNG THPT SỐ 1 NGHĨA HÀNH
ĐÁP ÁN ĐỀ THI THỬ - TN THPT 2025
Bài thi môn: TOÁN
(Đề gồm có 04 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề