TRƯỜNG THPT THANH BÌNH
---TỔ TOÁN---
ĐỀ THAM
KHẢO TN
THPT QG
NĂM 2024 -
2025
MÔN: TOÁN
Thời gian làm
bài: 90 phút;
Mã đề 121
Họ, tên thí sinh:..........................................................................Số báo danh:....................................
PHẦN I.Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho cấp số cộng có và . Công sai của cấp số cộng đó bằng
A. .B. .C. .D. .
Câu 2. Tập xác định của hàm số
6
log
=
y x
là
A.
[
)
0;
+
.B.
( )
0;
+
.C.
( )
;0
−
.D.
( )
;
− +
.
0.
>
x
( )
0; .D
= +
Câu 3. Tìm nghiệm của phương trình .
A. B. C. D.
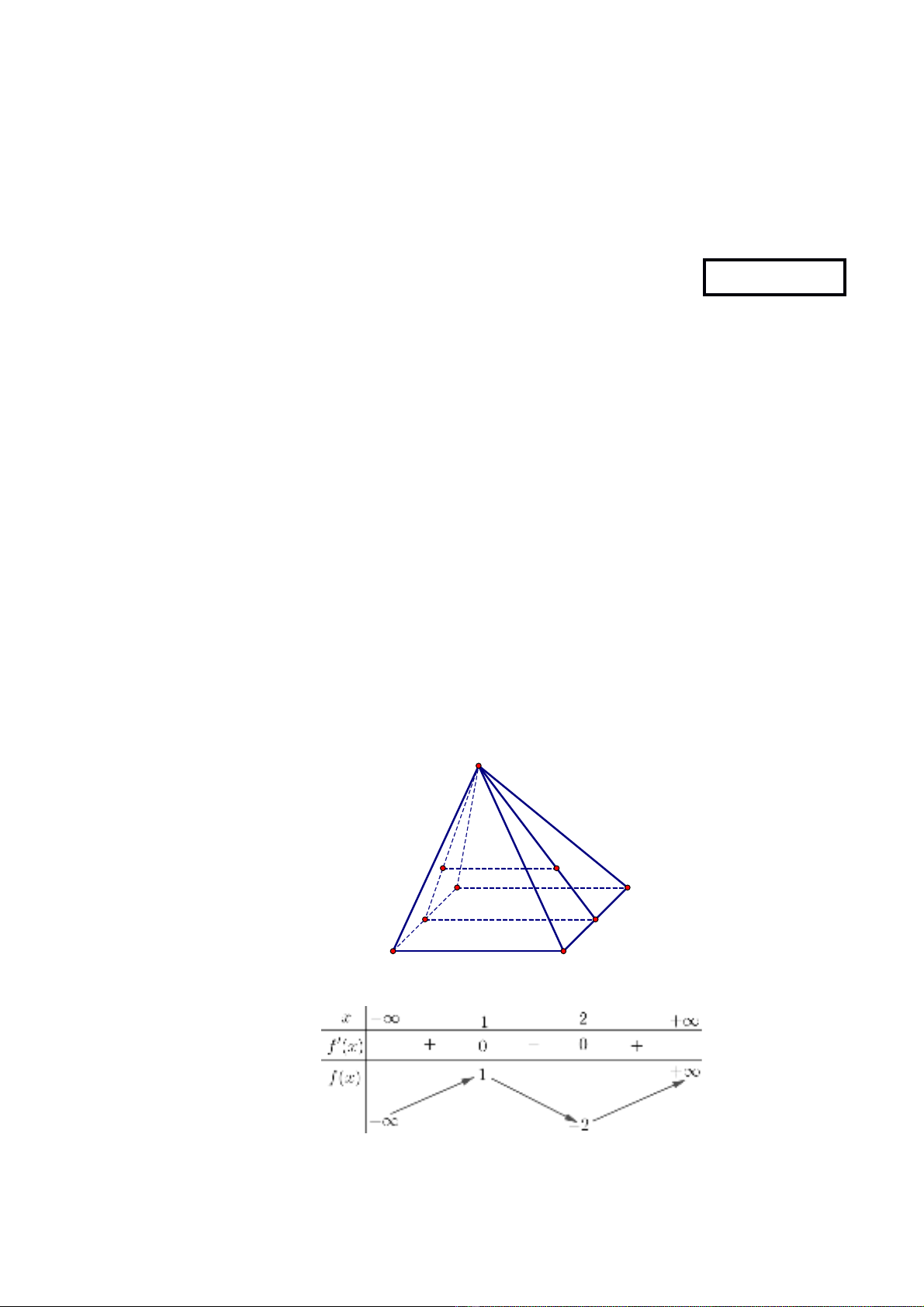
Câu 4. Cho hình chóp có đáy là hình chữ nhật. Gọi theo thứ tự là trọng tâm . Khi đó MN song
song với mặt phẳng
A. B. .C. D. .
N
M
F
E
B
C
A
S
Câu 5. Cho hàm số có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại
A. B. C. D.
Câu 6. Cho hàm số có và. Khẳng định đúng là
A. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
Mã Đề 121-Trang 1
B. Đồ thị hàm số đã cho không có tiệm cận ngang.
C. Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng và .
Câu 7. Hàm số là một nguyên hàm của hàm số trên khoảng . Khẳng định đúng là
A. B.
C. D.
Câu 8. Cho hàm số liên tục trên đoạn . Gọi là một nguyên hàm của hàm số trên đoạn . Khẳng
định nào sau đây là khẳng định sai?
A. .B. .
C. .D. .
Câu 9. Trong không gian , đường thẳng có một vectơ chỉ phương là
A. B. C. D.
Câu 10. Trong không gian cho mặt cầu Đường kính của bằng
A. B. C. D.
Câu 11. Cho hình hộp . Tìm giá trị của thích hợp điền vào đẳng thức vectơ sau:
A. B. C. D.
Câu 12. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được
ghi lại ở bảng sau:
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. .B. .C. .D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 12. Trong mỗi ý a), b), c),
d) ở mẫu câu, thí sinh chọn đúng hoặc sai.
Câu 1: Cho hàm số . Xét tính đúng sai của các khẳng định sau:
a) Với thì .
b) Phương trình có nghiệm .
c) Giá trị nhỏ nhất của hàm số là .
d) Phương trình chỉ có đúng một nghiệm .
Câu 2: Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,5 và
dự án 2 là 0,6. Khả năng thắng thầu của 2 dự án là 0,4. Gọi lần lượt là biến cố thắng
thầu dự án 1 và dự án 2.
a) và là hai biến độc lập.
Mã Đề 121-Trang 2
b) Xác suất công ty thắng thầu đúng 1 dự án là .
c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là .
d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án .
Câu 3: Cho hàm số . Gọi . Khi đó:
a) Với , thì .
b) Gọi thì ta có .
c) Biết và thì .
d) .
Câu 4: Trong không gian
Oxyz
, cho đường thẳng
:
∆
1
2 ,
3 3
x t
y t t
z t
= +
= +
= +
và mặt phẳng
( )
P
có
phương trình
2 2 0x y z
+ − − =
.
a) Một vectơ pháp tuyến của
( )
P
là
( )
1;2; 1 n
= −
r
.
b) Góc giữa
∆
và
( )
P
là
60
.
c) Chỉ có một điểm chung duy nhất giữa
∆
và
( )
P
.
d) Mọi điểm thuộc
∆
có hình chiếu lên
( )
P
là chính nó.
( )
P
( )
1; 2; 1 n
= −
r
∆
( )
1;1;3 u
=
r
( )
P
( )
1;2; 1 n
= −
r
( )
( )
( )
( )
2
2 2 2 2 2
1.1 2.1 1 .3
sin , 0
1 2 1 . 1 1 3
P
+ + −
∆ = =
+ + − + +
( )
( )
, 0P
∆ =
( )
1; 2;3 M
( )
0;1; 0 N
( )
( )
M
M P
N
N P
∆
∆
∆
( )
P
Mã Đề 121-Trang 3
∆
( )
P
∆
( )
P
PHẦN III.Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Cho hình chóp với đáy là hình thang vuông tại , đáy lớn , đáy nhỏ . vuông góc với
đáy, . Gọi là trung điểm của . là mặt phẳng qua và vuông góc với . Tìm diện tích thiết
diện của hình chóp cắt bởi mặt phẳng .
Câu 2: Cho đồ thị có trọng số như Hình bên.
Độ dài đường đi bằng bao nhiêu?
Câu 3: Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1
đáp án đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2
điểm. Một học sinh không học bài nên đánh tùy ý một câu trả lời. Tìm xác suất để học
sinh này nhận điểm dưới 1.
Câu 4: Giả sử chi phí cho xuất bản cuốn tạp chí được cho bởi công thức: trong đó được tính
theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số được gọi
là chi phí trung bình cho một cuốn tạp chí khi xuất bản cuốn và tổng chi phí cho cuốn
tạp chí. Tính theo và tìm số lượng tạp chí cần xuất bản sao cho chi phí trung bình là
thấp nhất, biết rằng nhu cầu hiện tại xuất bản không quá 30.000 cuốn. Khi đó chi phí
trung bình cho một cuốn tạp chí là bao nhiêu nghìn đồng?
Câu 5: Bạn An nhận thiết kế logo hình con mắt cho một cơ sở y tế: Logo là hình phẳng giới hạn
bởi hai parabol và như Hình 1. Bạn An cần tính diện tích của logo để báo giá cho cơ sở
y tế đó trước khi kí hợp đồng. Diện tích của logo là bao nhiêu decimet vuông (kết quả
làm tròn đến hàng phần chục)?
Mã Đề 121-Trang 4
Hình 1
Câu 6: Trong không gian
Oxyz
, cho mặt phẳng đi qua điểm và cắt các trục lần lượt tại sao
cholà trực tâm tam giác . Mặt phẳng có phương trình dạng . Tính tổng .
( )
α
,Ox
,Oy
Oz
( )
;0; 0 ,A m
( )
0; ;0 ,B n
( )
0;0;C p
, , 0m n p
( )
α
1
x y z
m n p
+ + =
( )
1 2 3 1Mm n p
α
+ + =
( )
1
( )
1 ; 2;3 ,AM m
= −
uuuur
( )
1; 2 ;3 ,BM n
= −
uuuur
( )
0; ; ,BC n p
= −
uuur
( )
;0;AC m p
= −
uuur
M
ABC
. 0 3 2 0
3 0
. 0
AM BC p n
p m
BM AC
= − =
− =
=
uuuur uuur
uuuur uuur
( )
2
( )
1
( )
2
14;m
=
7;n
=
14
3
p
=
( )
α
31 2 3 14 0
14 7 14
x y z x y z
+ + = + + − =
1 2 3 6T a b c
= + + = + + =
-----Hết-----
Mã Đề 121-Trang 5