NHÓM WORD & BIÊN SOẠN TOÁN ĐỀ THI THỬ:2022-2023
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 1
ĐỀ THI THỬ TN THPT– SỞ YÊN BÁI
NĂM HỌC 2022-2023
Môn: TOÁN – LỚP 12
Thời gian: 90 phút (Không kể thời gian phát đề
)
TRAO ĐỔI & CHIA SẺ
KIẾN THỨC
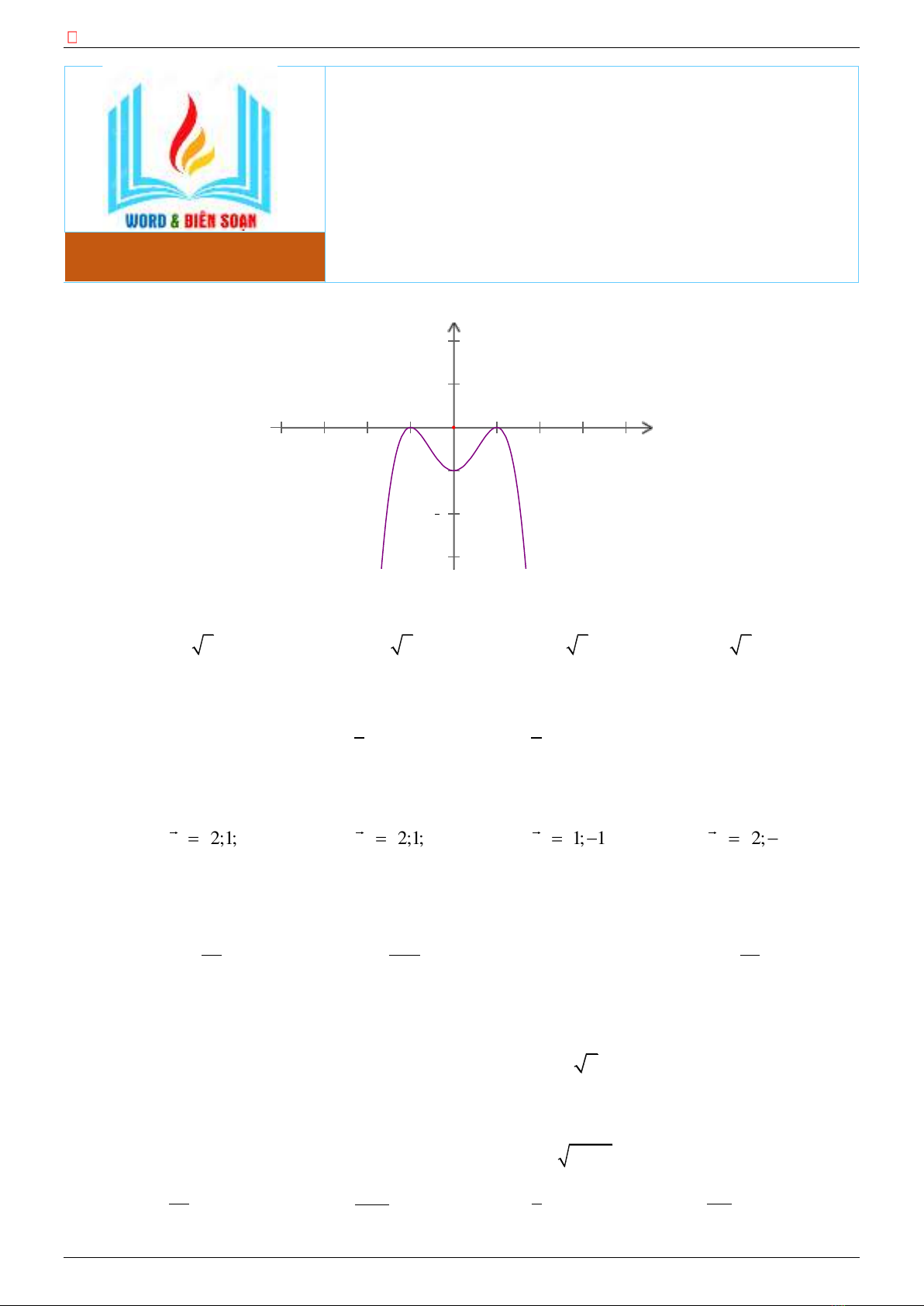
Câu 1. [MĐ1] Đồ thị của hàm số nào dưới đây có dạng như hình bên dưới?
A.
42
21y x x= − + −
B.
42
33y x x= + −
C.
21yx= − −
D.
32
32y x x= − + −
Câu 2. [MĐ1] Nghiệm phức có phần ảo âm của phương trình
là
A.
16i+
. B.
16i−+
. C.
16i−−
. D.
16i−
.
Câu 3. [MĐ1] Cho hình trụ có đường kính đáy là
2r
và độ dài đường cao
h
. Thể tích khối trụ đã cho
bằng
A.
2
rh
. B.
2
1
3rh
. C.
2
2
3rh
. D.
2rh
.
Câu 4. [MĐ1] Trong không gian
Oxyz
, cho mặt phẳng
( )
: 2 3 0P x y z+ − + =
có một vectơ pháp
tuyến là
A.
( )
12;1;3n=
. B.
( )
22;1; 1n=−
. C.
( )
31; 1;3n=−
. D.
( )
42; 1;3n=−
.
Câu 5. [MĐ1] cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
A
,
2AB a=
,
( )
SA ABC⊥
,
SA a=
. Thể tích của khối chóp
.S ABC
bằng
A.
3
2
a
V=
. B.
3
2
3
a
V=
. C.
3
2Va=
. D.
3
6
a
V=
.
Câu 6. [MĐ1] Trong không gian
Oxyz
, mặt cầu
( )
2 2 2
: 2 4 6 10 0S x y z x y z+ + − − + + =
có bán kính
là
A.
4R=
. B.
1R=
. C.
32R=
. D.
2R=
.
Câu 7. [MĐ2] Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
2x=
và
3x=
, biết rằng
khi cắt vật thể bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
bất kì
( )
23x
thì được thiết diện là một hình vuông có độ dài cạnh là
23x−
.
A.
10
3
. B.
10
3
. C.
8
3
. D.
8
3
.
2
2
y
x
1
-1
O
ĐỀ THI THỬ:2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 8. [MĐ2] Tiệm cận ngang của đồ thị hàm số
2
1
x
yx
−
=+
là đường thẳng có phương trình
A.
2y
=−
. B.
1x=−
. C.
1y=
. D.
2x=
.
Câu 9. [MĐ1] Cho cấp số cộng
( )
n
u
với
32u=
và
46u=
. Công sai của cấp số cộng đã cho bằng
A.
2−
. B.
4−
. C.
4
. D.
2
.
Câu 10. [MĐ2] Cho các số thực dương
,ab
thỏa mãn
logax=
,
logby=
. Tính
( )
23
log ab
.
A.
32
P x y=
. B.
23P x y=+
. C.
6P xy=
. D.
22
P x y=+
.
Câu 11. [MĐ1] Cho khối chóp có diện tích đáy
2
6Ba=
và chiều cao
2ha=
. Thể tích của khối chóp đã
cho bằng
A.
3
4a
. B.
3
6a
. C.
3
12a
. D.
3
3a
.
Câu 12. [MĐ2] Diện tích hình phẳng giới hạn bởi các đường
3
y x x=−
và
2
y x x=−
bằng
A.
9
4
. B.
37
12
. C.
81
12
. D.
13
.
Câu 13. [MĐ1] Cho hàm số bậc ba
( )
y f x=
có đồ thị như hình bên. Giá trị cực đại của hàm số đã cho
là
A.
1−
. B.
2
. C.
1
. D.
2−
.
Câu 14. [MĐ1] Cho hàm số
( )
fx
có đạo hàm
( ) ( )( )
2
' 1 4 ,f x x x x x= − +
. Số điểm cực trị của
hàm số đã cho là
A.
2
. B.
4
. C.
1
. D.
3
.
Câu 15. [MĐ1] Trong không gian
Oxyz
, góc giữa hai mặt phẳng
( )
Oxy
và
( )
Oxz
là
A.
60
. B.
30
. C.
90
. D.
45
.
Câu 16. [MĐ1] Số phức liên hợp của số phức
3 12zi=−
A.
3 12zi= − −
. B.
3 12zi= − +
. C.
3 12zi=+
. D.
3 12zi=−
.
Câu 17. [MĐ1] Trong không gian
Oxyz
, phương trình đường thẳng
đi qua điểm
( )
2;0; 1M−
và có
một vectơ chỉ phương
( )
4; 6;2a=−
là
A.
42
63
2
xt
yt
zt
=+
= − −
=+
. B.
22
3
1
xt
yt
zt
=+
=−
= − +
. C.
24
6
12
xt
yt
zt
= − +
=−
=+
. D.
22
3
1
xt
yt
zt
= − +
=−
=+
.
Câu 18. [MĐ1] Cho hàm số
( )
sin 3x
f x x=−
. Khẳng định nào đúng?
A.
( )
d cos 3 ln3
x
f x x x C= + +
. B.
( )
3
d cos ln 3
x
f x x x C= − − +
.
C.
( )
3
d sin ln3
x
f x x x C= − +
. D.
( )
d cos 3 ln3
x
f x x x C= − +
.
NHÓM WORD & BIÊN SOẠN TOÁN ĐỀ THI THỬ:2022-2023
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 3
Câu 19. [MĐ1] Nếu
( )
2
1
d3f x x
−
=
và
( )
2
1
d5g x x
−
=−
thì
( ) ( )
2
1
3dI f x g x x
−
=−


là
A.
14I=
. B.
4I=
. C.
4I=−
. D.
10I=−
.
Câu 20. [MĐ1] Với mọi
0x
, đạo hàm của hàm số
1
x
ye=
là
A.
1
2
1x
ye
x
=−
. B.
1
x
e
yx
=
. C.
1
1x
ye
x
=−
. D.
1
2
1x
ye
x
=
.
Câu 21. [MĐ1] Với
a
là số thực dương tùy ý,
5
a
bằng
A.
2
5
a
. B.
5
a
. C.
5
2
a
. D.
2
a
.
Câu 22. [MĐ1] Có bao nhiêu số có năm chữ số khác nhau được tạo thành từ các chữ số
1,2,3,4,5,6
?
A.
5
6
A
. B.
5
P
. C.
5
6
C
. D.
6
P
.
Câu 23. [MĐ1] Cho hàm số
( )
y f x=
có bảng biến thiên sau:
Hàm số đã cho đồng biến trên khoảng
A.
( )
0;1
. B.
( )
;1− −
. C.
( )
1;− +
. D.
( )
;1−
.
Câu 24. [MĐ2] Cho số phức
z
thỏa mãn
( )
( )
2 4 8 19i z z i i+ − − = − +
. Mô đun của
z
bằng
A.
13
. B.
5
. C.
5
. D.
13
.
Câu 25. [MĐ1] Nghiệm của phương trình
( )
4
log 3 2 2x−=
là
A.
7
2
. B.
6
. C.
10
3
. D.
3
.
Câu 26. [MĐ2] Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh bằng
a
,
( )
SA ABC⊥
,
3SA a=
. Tính góc giữa đường thẳng
SB
và mặt phẳng
( )
ABC
.
A.
30
. B.
75
. C.
60
. D.
45
.
Câu 27. [MĐ2] Cho hàm số
( )
fx
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
( )
2 3 0fx−=
là
A. 1. B. 0. C. 2. D. 3.
Câu 28. [MĐ1] Cho hai số phức
12
3 4 , 1z i z i= − = −
. Phần ảo của số phức
12
.zz
bằng
A.
1−
. B.
1
. C.
7
. D.
7−
.
ĐỀ THI THỬ:2021-2022 NHÓM WORD & BIÊN SOẠN TOÁN
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 29. [MĐ2] Khối cầu đường kính
4a
có thể tích bằng
A.
3
32
3
a
. B.
3
16 a
. C.
3
8
3
a
. D.
3
6a
.
Câu 30. [MĐ2] Trong không gian
Oxyz
, cho điểm
( )
3; 1; 2M−−
và mặt phẳng
( )
:3 2 4 0.P x y z− + + =
Phương trình mặt phẳng đi qua
M
và song song với
( )
P
là
A.
3 2 6 0x y z− + − =
. B.
3 2 6 0x y z− + + =
. C.
3 2 6 0x y z− − − =
. D.
3 2 14 0x y z+ − − =
.
Câu 31. [MĐ1] Trong không gian
Oxyz
, cho điểm
( )
2; 5;4 .M−
Tọa độ điểm
M
đối xứng với
M
qua mặt phẳng
( )
Oyz
là
A.
( )
2; 5; 4−−
. B.
( )
2;5;4
. C.
( )
2; 5;4−−
. D.
( )
2;5; 4−
.
Câu 32. [MĐ1] Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
1 2 5
:?
2 3 4
x y z
d− + −
==
A.
( )
1;2; 5Q−−
. B.
( )
2;3;4P
. C.
( )
1;2;5M
. D.
( )
1; 2;5N−
.
Câu 33. [MĐ1] Cho
( )
3
x dx F x C=+
. Khẳng định nào đúng?
A.
( )
4
4
x
Fx
=
. B.
( )
3
3
x
Fx
=
. C.
( )
3
F x x
=
. D.
( )
2
3F x x
=
.
Câu 34. [MĐ2] Một hộp chứa 4 viên bi trắng, 5 viên bi đỏ và 6 viên bi xanh. Lấy ngẫu nhiên từ hộp ra
4 viên bi. Xác suất để 4 viên bi được chọn có đủ ba màu và số bi đỏ nhiều nhất là
A.
8
91
. B.
20
91
. C.
16
91
. D.
12
91
.
Câu 35. [MĐ2] Tập nghiệm của bất phương trình
23
149
7
xx−



là
A.
(
)
;1 2;− +
. B.
( )
1;2
. C.
1;2
. D.
)
0; +
.
Câu 36. [MĐ3] Có bao nhiêu số nguyên
x
thỏa mãn
22
52
2023 2023
log log
8 125
xx−−
?
A.
26
. B.
25
. C.
27
. D.
24
.
Câu 37. [MĐ3] Trong không gian
Oxyz
, cho các điểm
( ) ( ) ( )
1;0;2 , 1;1;3 , 3;2;0A B C−
và mặt phẳng
( )
: 2 2 1 0P x y z+ − + =
. Biết rằng điểm
( )
;;M a b c
thuộc mặt phẳng
( )
P
sao cho biểu thức
2 2 2
2MA MB MC+−
đạt giá trị nhỏ nhất. Khi đó
abc++
bằng
A.
1−
. B.
5
. C.
3
. D.
1
.
Câu 38. [MĐ3] Có bao nhiêu số thực
m
để hàm số
4 3 2
3 4 12y x x x m= − − +
có giá trị nhỏ nhất trên
đoạn
3;2−
bằng 10?
A. 1. B. 3. C. 4. D. 2.
Câu 39. [MĐ3] Cho hàm số
()y f x=
liên tục trên
( 1; )− +
thỏa mãn
1
( ) 2( 1). ( ) 1
f x x f x x
+ + = +
và
(0) 1f=
. Giá trị của
(3)f
bằng
A.
1
2ln 2 2
+
. B.
11
ln3
22
+
. C.
11
ln 2
22
+
. D.
1 ln2+
.
Câu 40. [MĐ3] Cho phương trình
( )
2
2 2 3
4log 11.log 20 . log 0x x x m− − + =
(
m
là tham số thực). Có
bao nhiêu giá trị nguyên của
m
để phương trình đã cho có đúng hai nghiệm phân biệt?
A. Vô số. B.
4
. C.
3
. D.
2
.
NHÓM WORD & BIÊN SOẠN TOÁN ĐỀ THI THỬ:2022-2023
TÀI LIỆU ÔN THI THPT QUỐC GIA Trang 5
Câu 41. [MĐ3] Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa mặt bên và mặt phẳng
đáy bằng
60
. Tính khoảng cách từ điểm A đến mặt phẳng
( )
SBC
.
A.
3a
. B.
23a
. C.
3
3
a
. D.
3
2
a
.
Câu 42. [MĐ3] Biết
( )
Fx
và
( )
Gx
là hai nguyên hàm của
( )
fx
trên và
( ) ( ) ( ) ( )
5
0
d 5 0 3 0f F G m mxx = − +
. Gọi
S
là diện tích hình phắng giới hạn bởi các đường
( ) ( )
, , 0y F x y G x x= = =
và
5x=
. Khi
45S=
thì m bằng
A. 4. B. 2. C. 1. D. 3.
Câu 43. [MĐ3] Trên tập số phức, xét phương trình
22
4 2 0z az b− + + =
(
,ab
là các tham số thực). Có
bao nhiêu cặp số thực
( )
;ab
sao cho phương trình đó có hai nghiệm
1
z
,
2
z
thỏa mãn
12
2 3 3z iz i+ = +
?
A. 1. B. 2. C. 3. D. 4.
Câu 44. [MĐ2] Có bao nhiêu giá trị nguyên của
m
thuộc khoảng
( )
5;5−
để hàm số
( )
42
2 2 1 10y x m x= − + +
có ba điểm cực trị?
A. 5. B. 10. C. 6. D. 0.
Câu 45. [MĐ3] Cho hàm số
( )
32
4 9 5y x mx m x= − − + + +
, với
m
là tham số. Có bao nhiêu giá trị
nguyên của
m
để hàm số nghịch biến trên
( )
;− +
?
A.
4
. B.
7
C.
5
. D.
6
.
Câu 46. [MĐ3] Cho số phức
z
thỏa mãn
2 5 2 5z i z i− + + − =
. Gọi giá trị lớn nhất và giá trị nhỏ nhất
của biểu thức
1 3 2T z i z i= − − + − −
tương ứng là
M
và
m
. Giá trị của
Mm+
bằng
A.
37 2 5+
. B.
37 5 6 2++
. C.
2 13 4 5+
. D.
37 2 10+
.
Câu 47. [MĐ2] Cho khối lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông cân tại
B
,
AB a=
. Biết khoảng cách từ
A
đến mặt phẳng
( )
A BC
bằng
6
3a
. Thể tích khối lăng trụ
đứng
.ABC A B C
.
A.
3
2
6a
. B.
3
2
2a
. C.
3
2a
. D.
3
2
4a
.
Câu 48. [MĐ3] Trong không gian
Oxyz
, cho ba điểm
( ) ( ) ( )
2;1;0 , 4;4; 3 , 2;3; 2A B C− − −
và đường
thẳng
1 1 1
:2 2 1
x y z
d− − −
==
−−
. Gọi
( )
là mặt phẳng chứa
d
sao cho
,,A B C
ở cùng phía đối
với mặt phẳng
( )
. Gọi
1 2 3
,,d d d
lần lượt là khoảng cách từ
,,A B C
đến
( )
. Tìm giá trị lớn
nhất của
1 2 3
23T d d d= + +
.
A.
max 6 14T=
. B.
max 203T=
.
C.
max 2 21T=
. D.
max
203
14 3 21
3
T= + +
.
Câu 49. [MĐ3] Có bao nhiêu giá trị nguyên của tham số
m
trong khoảng
( )
;10−
để hàm số
4
3
mx
yxm
+
=++
đồng biến trên khoảng
( )
1; +
?
A.
9
. B.
8
. C.
0
. D.
10
.