Đ s 1ề ố
Đ THI H C KÌ 2 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 10ớ
Th i gian làm bài 90 phútờ
A-PH N CHUNG: (7.0ĐI M)Ầ Ể
CÂU 1: (1.0 ĐI M) Xét bi u th c f(x) = (3xỂ ể ứ 2 – 7x + 2)(1 – x)
CÂU2 : (2.5 ĐI M) Gi i b t ph ng trìnhỂ ả ấ ươ
a)
xx 21
3
23
2
−
>
−
b)
725 <−x
CÂU 3: (1.5 ĐI M) Cho ph ng trình: 2xỂ ươ 2 – (m+1)x + 3m2 – 8m + 4 = 0
Tìm m đ ph ng trình có hai nghi m trái d u.ể ươ ệ ấ
CÂU 4: (2.0 ĐI M) Đi u tra v đi n năng tiêu th trong m t tháng (tính theo kw/h)Ể ề ề ệ ụ ộ
c a 20 gia đình m t khu v c, ng i ta thu đ c m u s li u sau:ủ ở ộ ự ườ ượ ẫ ố ệ
80 45 65 45 70 50 80 70 65 80
50 70 45 85 85 75 50 65 85 65
a) l p b ng phân b t n s - l n su t m u s li u trên.ậ ả ố ầ ố ầ ấ ẫ ố ệ
b) Tính m c tiêu th đi n năng trung bình c a 20 gia đình, m t c a m u s li uứ ụ ệ ủ ố ủ ẫ ố ệ
trên?
B. PH N RIÊNG : (3.0 ĐI M)Ầ Ể Thí sinh ch làm m t trong hai ph n riêngỉ ộ ầ
Theo ch ng trình c b nươ ơ ả
CÂU 5a: Trong m t ph ng Oxy, cho tam giác ABC có A(4; –5), B(1; 3), C(3; –2)ặ ẳ
Vi t ph ng trình đ ng th ng trong các tr ng h p sau:ế ươ ườ ẳ ườ ợ
a) Đi qua hai đi m A, B.ể
b) Ch a đ ng cao AH c a tam giác ABC.ứ ườ ủ
CÂU 5b: Trong m t ph ng Oxy, cho đ ng th ng ặ ẳ ườ ẳ
∆
: 3x – 4y + 7 = 0
L p ph ng trình đ ng tròn có tâm I(2; –3) và ti p xúc v i đ ng th ng ậ ươ ườ ế ớ ườ ẳ
∆
.
Theo ch ng trình nâng caoươ
CÂU 6a: Trong m t ph ng Oxy, cho A(1; -2), B(3; 6).ặ ẳ
a) Vi t ph ng trình đ ng th ng qua A và song song v i đ ng th ng:ế ươ ườ ẳ ớ ườ ẳ
3x – 4y + 12 = 0.
b) Vi t ph ng trình đ ng th ng qua M (1; 3) và cách đ u hai đi m A,B.ế ươ ườ ẳ ề ể
CÂU 6b: L p ph ng trình đ ng tròn đi qua đi m A(1; 2), B(5; 2), C(1; –3)ậ ươ ườ ể
-----------------------------------H T-----------------------------------------Ế
H TÊN H C SINH:……………………………………….SBD:………….L P………Ọ Ọ Ớ
ĐÁP ÁN
A. PH N CHUNGẦ
CÂU N I DUNGỘĐI MỂ
1 1đ Xét d u bi u th c f(x) = (3xấ ể ứ 2 – 7x + 2)(1 – x)
3
1
,20273 2==⇒=+− xxxx
1- x = 0
⇒
x = 1
BXD:
x
∞−
3
1
1 2
∞+
3x2 – 7x +2 + 0 – – 0 +
1 – x + + 0 – –
f(x) + 0 – 0 + 0 –
f(x) = 0 khi x
2,1,
3
1=== xx
f(x) > 0 khi x
f(x) < 0 khi x
( )
+ ∞∪
∈;21;
3
1
0.25
0.5
0.25
2 a)
1.5đ
xx 21
3
23
2
−
>
−
0
)21)(23(
)23(3)21(2 >
−−
−−−
⇔xx
xx
0
)21)(23(
813 >
−−
+−
⇔xx
x
13
8
0813 =⇒=+− xx
3
2
03 =⇒=− xxx
2
1
021 =⇒=− xx
BXD:
x
∞−
2
1
13
8
3
2
∞+
–13x+8 + + 0 – –
3x–2 – – – 0 +
1–2x + 0 – – –
0.25
0.25
0.25
0.5
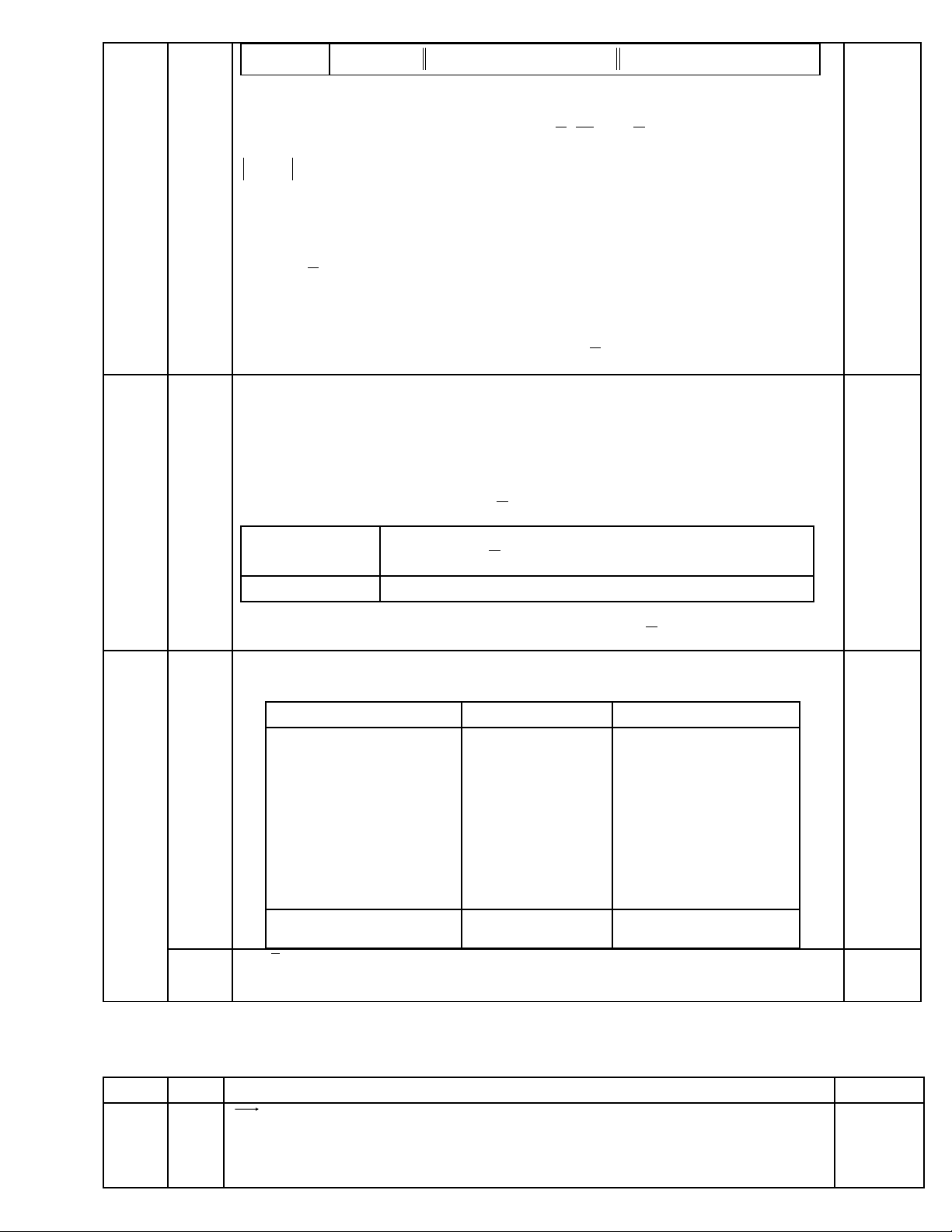
b)
1đ
VT – + 0 – +
T p nghi m b t ph ng trình Sậ ệ ấ ươ
+ ∞∪
=;
3
2
13
8
;
2
1
725 ≤−x
−≥−
≤−
⇔725
725
x
x
−≥
≤
⇔
1
5
9
x
x
T p nghi m bát ph ng trình S = ậ ệ ươ
−5
9
;1
0.25
0.5
0.25
0.25
3 1.5đ Tìm m đ ph ng trình 2xể ươ 2 – (m+1)x + 3m2 – 8m + 4 = 0
Có 2 nghi m trái d uệ ấ
Đ ph ng trình có 2 nghi m trái d u ể ươ ệ ấ ⇔ a.c < 0
⇔2(3m2 – 8m + 4 ) < 0
3m2 – 8m + 4 = 0 ⇒ m =
3
2
, m = 2
m
∞−
3
2
2 +∞
3m2 – 8m + 4 + 0 – 0 +
Đ ph ng trình có 2 nghi m trái d u ể ươ ệ ấ ⇔
3
2
< m < 2
0.25
0.25
0.25
0.5
0.25
4 a)
1đ
80 45 65 45 70 50 80 70 65 80
50 70 45 85 85 75 50 65 85 65
Đi n năng tiêu thệ ụ T n sầ ố T n su tầ ấ
45
50
65
70
75
80
85
3
3
4
3
1
3
3
15
15
20
15
5
15
15
C ngộ20 100%
0.5
0.5
b)
1đ
x
= 66,25 Kwh
M0 = 65
0.5
0.5
B. PH N RIÊNGẦ
Ch ng trình c b nươ ơ ả
5a a) A(4;–5); B(1;3); C(3;–2)
1đ
AB
=(–3; 8)
PTTS AB:
+−=
−=
ty
tx
85
34
0.5
0.5
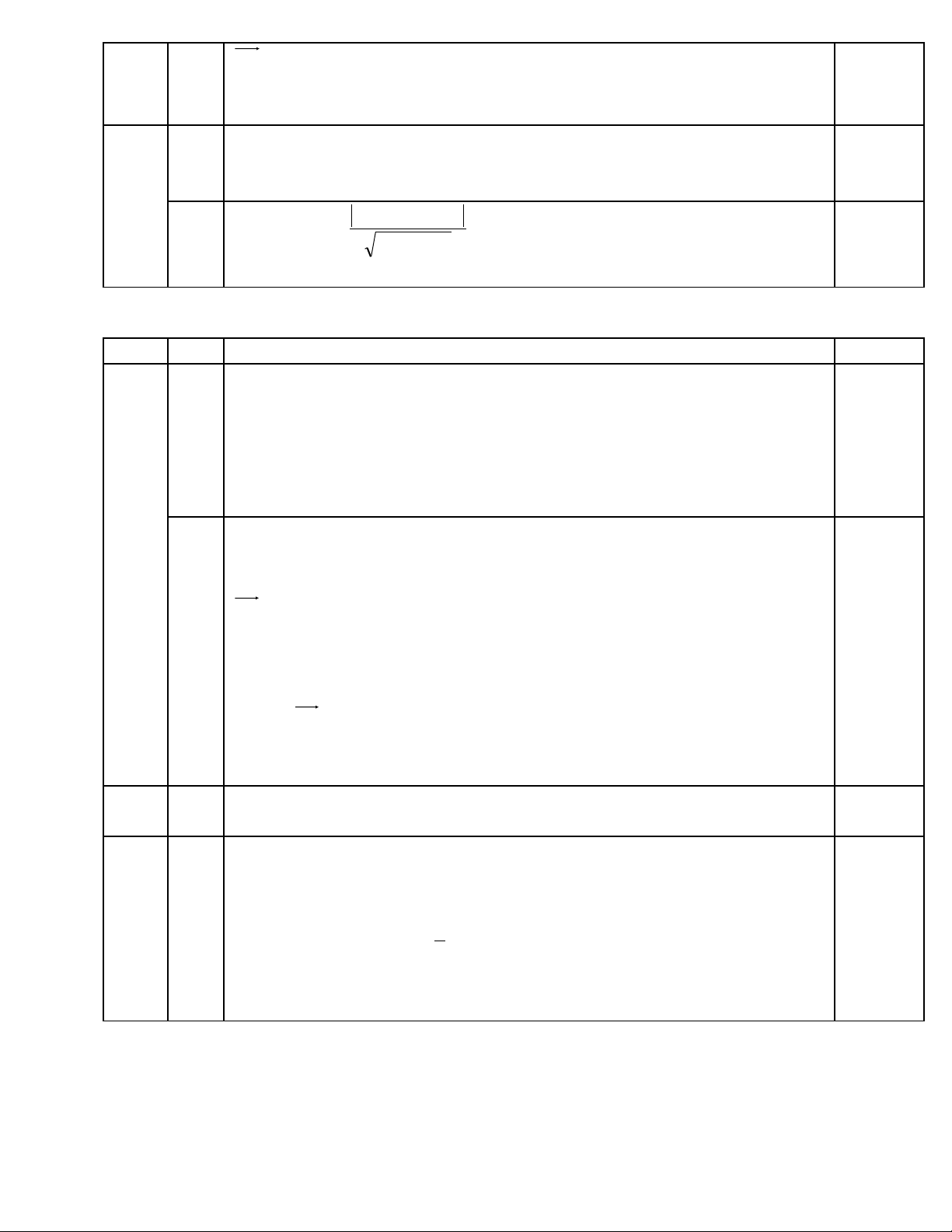
b)
1đ
BC
=( 2; –5)
PT AH: 2(x – 4) – 5(y + 5) = 0
⇔ 2x – 5y – 33 = 0
0.5
0.25
0.25
6a Cho đ ng th ng ườ ẳ
∆
: 3x – 4y + 7 = 0
L p ph ng trình đ ng tròn có tâm I(2; –3) và ti p xúc v iậ ươ ườ ế ớ
đ ng th ng ườ ẳ
∆
.
1đ R = d(I;∆) =
22 )4(3
7)3(42.3
−+
+−−
= 5
PTĐTròn: (x – 2)2 +(y + 3)2 = 25
0.5
0.5
Ch ng trình nâng caoươ
5b a) Trong m t ph ng Oxy, cho A(1; -2), B(3; 6).ặ ẳ
1đ Vi t ph ng trình đ ng th ng qua A và song song v i đ ngế ươ ườ ẳ ớ ườ
th ng: 3x – 4y + 12 = 0.ẳ
+Đ ng th ng song song v i 3x – 4y + 12 = 0. có d ngườ ẳ ớ ạ
3x – 4y + c = 0
+Qua A(1; – 2) : 3.1 – 4(–2) + c = 0 ⇔ c = –11
PTĐT: 3x – 4y –11 = 0.
0.5
0.5
b)
1đ
Vi t ph ng trình đ ng th ng qua M (1; 3) và cách đ u haiế ươ ườ ẳ ề
đi m A,B.ể
+d qua M(1; 3) và song song v i ABớ
AB
= (2;8)
PTTS c a d: ủ
+=
+=
ty
tx
83
21
+d qua M và trung đi m I c a ABể ủ
I(2;2),
MI
=(1;–1)
PTTS:
−−=
+=
ty
tx
1
1
0.25
0.25
0.25
0.25
6b L p ph ng trình đ ng tròn đi qua đi m A(1; 2), B(5; 2), C(1; –ậ ươ ườ ể
3)
1đ PTĐTròn có d ng: xạ2 +y2 – 2ax –2by + c = 0
Th t a đ A,B,C ta đ c h ph ng trìnhế ọ ộ ượ ệ ươ
=−−
=−+
=−+
1062
29410
542
cba
cba
cba
⇒
−=
=
=
1
2
1
3
c
b
a
PTĐTròn: x2 + y2 – 6x + y –1 = 0
0.25
0.5
0.25
Đ s 2ề ố
Đ THI H C KÌ 2 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 10ớ
Th i gian làm bài 90 phútờ
I. Ph n chung:ầ (7,0 đi m)ể
Câu 1: (2,0 đi m) Gi i các b t ph ng trình sau:ể ả ấ ươ
a)
x x
x x
2
2
2 7 15 0
3 7 2
+ −
− +
b)
x x x
2
4 4 2 1 5+ − +
Câu 2: (1,0 đi m) Tìm ểm đ b t ph ng trình sau nghi m đúng v i m i ể ấ ươ ệ ớ ọ x ∈ R:
m x m x
2 2
( 2) 2( 2) 2 0+ − − +
Câu 3: (1,0 đi m) S ti t t h c t i nhà trong 1 tu n c a m t nhóm 20 h c sinh đ c cho trong b ngể ố ế ự ọ ạ ầ ủ ộ ọ ượ ả
sau:
9 1
5
1
1
1
2
1
6
1
2
1
0
1
4
1
4
1
5
1
6
1
3
1
6
8 9 1
1
1
0
1
2
1
8
18
a) L p b ng phân b t n s c a b ng s li u trên.ậ ả ố ầ ố ủ ả ố ệ
b) Tính s trung bình và ph ng sai c a b ng s li u đó.ố ươ ủ ả ố ệ
Câu 4: (1,0 đi m) Cho 2 s ể ố x, y tho mãn ả
x y 0+
. Ch ng minh b t đ ng th c:ứ ấ ẳ ứ
x y x y xy
5 5 4 4 0+ − −
Câu 5: (2,0 đi m) Trong m t ph ng v i h to đ Oể ặ ẳ ớ ệ ạ ộ xy, cho ∆ABC có t a đ các trung đi m c a cácọ ộ ể ủ
c nh AB, BC, CA l n l t là M(2; 1), N(5; 3), P(3; –4).ạ ầ ượ
a) Tìm to đ các đ nh A, B, C c a tam giác ABC.ạ ộ ỉ ủ
b) Vi t ph ng trình đ ng tròn có tâm A và đi qua đi m B.ế ươ ườ ể
II. Ph n riêngầ (3,0 đi m)ể
1. Theo ch ng trình Chu nươ ẩ
Câu 6a: (2,0 đi m) ể
a) Rút g n bi u th c:ọ ể ứ A =
x x x
2
cos cos sin
4 4
π π
� � � �
+ − +
� � � �
� � � �
b) Cho
x x 1
sin cos 2
+ =
. Tính giá tr bi u th c ị ể ứ B =
xsin2
.
Câu 7a: (1,0 đi m) Cho ể∆ABC có đ dài các c nh BC = ộ ạ a, CA = b, AB = c.
Ch ng minh r ng n u:ứ ằ ế
b b a c a c
2 2 2 2
( ) ( )− = −
thì
ﾵ
A0
60=
.
2. Theo ch ng trình Nâng caoươ
Câu 6b: (2,0 đi m)ể
a) Đ n gi n bi u th c:ơ ả ể ứ C =
a a a
a a a
sin sin4 sin7
cos cos4 cos7
+ +
+ +