6
Hình 7.7
IV.5. Đường dây:
IV.5.1. Đường dây trên không:
z X2 = X1
z Xo phụ thuộc đường đi của dòng thứ thự không, nghĩa là phụ thuộc vào sự phân
bố của chúng trong đất, trong dây trung tính, trong những mạch nối đất song song (dây
chống sét). Hỗ cảm giữa các pha làm giảm X1, X2 nhưng làm tăng Xo.
- Đối với đường dây đơn 3 pha (1 lộ): Xo > X1
- Đối với đường dây kép 3 pha (2 lộ), X’o của một lộ lớn hơn điện kháng thứ
tự không Xo của đường dây đơn 3 pha do có hỗ cảm giữa 2 mạch song song:
X’o = Xo + XI-IIo
trong đó: XI-IIo - điện kháng thứ tự không hỗ cảm giữa 2 lộ.
Điện kháng tương đương của 1 pha đường dây kép là:
X’’o = X’o/2 = (Xo + XI-IIo)/2
- Anh hưởng của dây chống sét:
Dây chống sét thường được nối đất ở mỗi cột tạo thành những mạch vòng kín cho
dòng cảm ứng đi qua khi có dòng thứ tự không trong các pha (đối với dòng thứ tự thuận
và dòng thứ tự nghịch không có cảm ứng vì tổng từ thông móc vòng do chúng tạo nên
bằng không).
Chính hỗ cảm giữa dây chống sét và các pha làm giảm Xo của đường dây, hỗ cảm
này phụ thuộc vào vật liệu, số lượng và sự bố trí của dây chống sét. Trong tính toán gần
đúng có thể lấy trị số trung bình trong bảng 7.2.
Bảng 7.2:
TÍNH CHấT ĐƯờNG DÂY Tỷ Số Xo/X1
Đường dây đơn không có dây chống sét 3,5
Đường dây đơn có dây chống sét bằng thép 3
Đường dây đơn có dây chống sét dẫn điện tốt 2
Đường dây kép không có dây chống sét 5,5
Đường dây kép có dây chống sét bằng thép 4,7
Đường dây kép có dây chống sét dẫn điện tốt 3
7
IV.5.1. Đường dây cáp:
Võ cáp thường được nối đất ở 2 đầu và nhiều điểm trung gian (hộp nối cáp), do đó
tạo thành đường đi đối với dòng thứ tự không, võ cáp có ảnh hưởng tương tự như dây
chống sét của đường dây trên không. Giá trị ro, Xo của dây cáp thay đổi trong phạm vi
rộng. Trong tính toán gần đúng, với cáp 3 lõi có thể xem:
ro ≈ 10r1
Xo ≈ (3,5 ÷ 4,6)X1
V. Sơ đồ Các thành phần thứ tự:
V.1. Sơ đồ thứ tự thuận và thứ tự nghịch:
Sơ đồ thứ tự thuận là sơ đồ dùng để tính toán ở chế độ đối xứng. Tùy thuộc vào
phương pháp và thời điểm tính toán, các máy phát và các phần tử khác được thay thế
bằng sức điện động và điện kháng tương ứng.
Sơ đồ thứ tự nghịch và sơ đồ thứ tự thuận có cấu trúc tương tự nhau vì đường đi của
dòng thứ tự nghịch và dòng thứ tự thuận là như nhau. Điểm khác biệt của sơ đồ thứ tự
nghịch so với sơ đồ thứ tự thuận là:
- các nguồn sức điện động bằng không.
- các điện kháng thứ tự nghịch không thay đổi, không phụ thuộc vào dạng ngắn
mạch và thời điểm tính toán.
Ta gọi:
z Điểm đầu của sơ đồ thứ tự thuận và thứ tự nghịch là điểm nối tất cả các trung tính
máy phát và phụ tải, đó là điểm có thế điện bằng không.
z Điểm cuối của sơ đồ thứ tự thuận và thứ tự nghịch là điểm sự cố.
z Điện áp giữa điểm cuối và điểm đầu của sơ đồ thứ tự thuận và thứ tự nghịch tương
ứng là điện áp ngắn mạch thứ tự thuận và thứ tự nghịch.
V.2. Sơ đồ thứ tự không:
Đường đi của dòng thứ tự không rất khác với dòng thứ tự thuận và thứ tự nghịch.
Sơ đồ thứ tự không phụ thuộc rất nhiều vào cách nối dây của máy biến áp và chế độ nối
đất điểm trung tính của hệ thống điện.
Muốn thành lập sơ đồ thứ tự không cần bắt đầu từ điểm ngắn mạch, coi rằng cả 3
pha tại điểm đó nhập chung và có điện áp là UNo. Sơ đồ thứ tự không chỉ bao gồm các
phần tử mà dòng thứ tự không có thể đi qua. Tổng trở nối đất các điểm trung tính cần
nhân 3, vì sơ đồ thứ tự không được lập cho 1 pha trong khi qua tổng trở nối đất có dòng
thứ tự không của cả 3 pha.
VI. Tính toán các dạng ngắn mạch cơ bản:
Qui ước:
- Coi pha A là pha đặc biệt (ở trong điều kiện khác 2 pha còn lại).
- Xét ngắn mạch ngay tại đầu nhánh rẽ của phần tử và chiều dương của dòng điện là
từ các pha đến điểm ngắn mạch.
Theo điều kiện phân tích hệ thống véctơ không đối xứng, ta đã có:
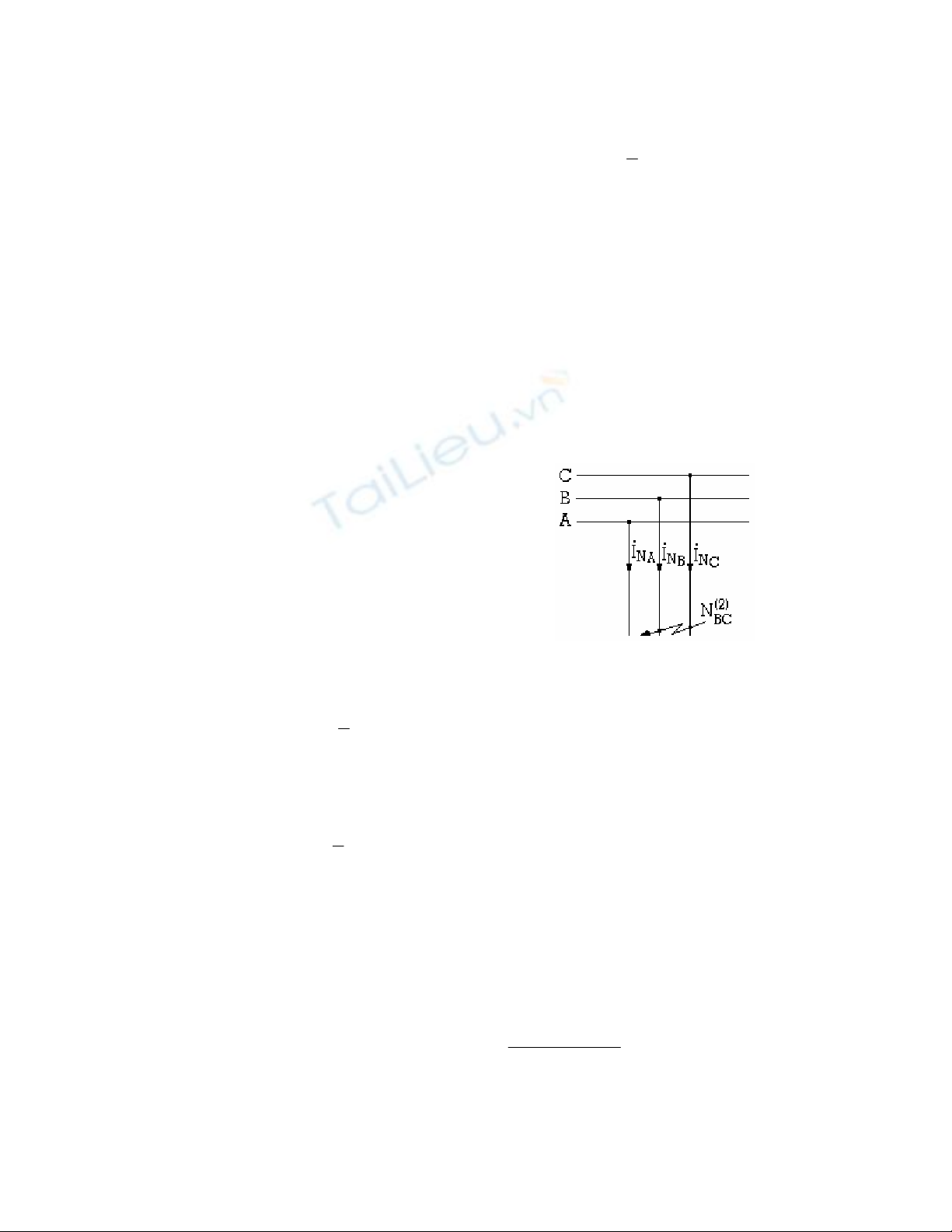
8
I
I
I
aa
aa
I
I
I
NA
NB
NC
N
NA
NA
.
.
.
.
.
.
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
111
1
1
2
2
0
1
2
và
I
I
I
aa
aa
I
I
I
N
NA
NA
NA
NB
NC
.
.
.
.
.
.
0
1
2
2
2
1
3
111
1
1
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
và các phương trình cơ bản:
UEjIX
UjI
UjI
NA A NA
NA NA
NN
...
..
..
.
.
.
11
1
22
2
00
0
0
0
=−
=−
=−
ΣΣ
Σ
Σ
X
X
(7.1)
(7.2)
(7.3)
VI.1. Ngắn mạch 2 pha:
Xét ngắn mạch giữa 2 pha B,
C (hình 7.8). Điều kiện ngắn mạch
là:
I
II
UU
NA
NB NC
NB NC
.
..
..
(7.4)
(7.5)
(7.6)
=
=−
=
0
Thay vào các phương trình
thứ tự:
Hình 7.8
U
U
U
aa
aa
U
U
U
UU
N
NA
NA
NA
NB
NB
NA NA
.
.
.
.
.
.
..
0
1
2
2
2
12
1
3
111
1
1
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⇒
= (7.7)
I
I
I
aa
aa
I
I
I
II
N
NA
NA
NB
NB
N
NA NA
.
.
.
.
.
.
..
0
1
2
2
2
0
12
1
3
111
1
1
00
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⇒=
=−
(7.8)
(7.9)
Giải các phương trình từ (7.1) đến (7.9) ta có:
EjIX jIX jIX
ANA NA NA
.. . .
.
ΣΣΣ
−=− +
112212
00.= .
Σ
Như vậy:
IE
jX X
NA A
..
()
1
12
=+
Σ
ΣΣ
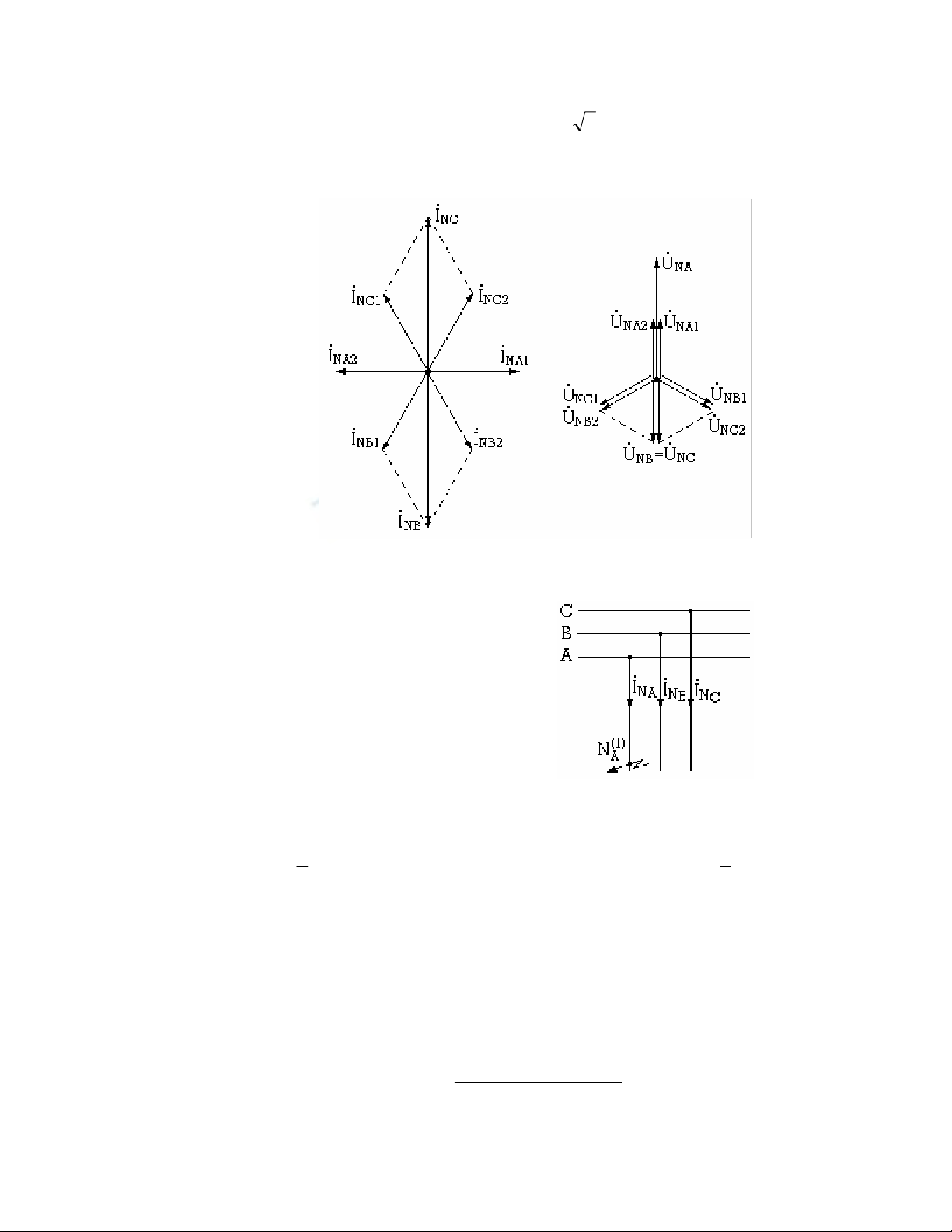
9
;
;
IIjI
UU jIX U
UU UUU
NB NC NA
NA NA NA N
NA NA NB NC NA
.. .
.. . .
.. ...
.
=− =−
==
==
3
0
2
1
121
20
11
Σ=
=−
Hình 7.9
VI.2. Ngắn mạch 1 pha:
Xét ngắn mạch 1 pha ở pha
A (hình 7.10). Điều kiện ngắn
mạch là:
I
I
U
NB
NC
NA
.
.
.
(7.10)
(7.11)
(7.12)
=
=
=
0
0
0
Thay vào phương trình thứ tự
dòng:
Hình 7.10
I
I
I
aa
aa
I
II I I
N
NA
NA
NA
NNANA NA
.
.
.
.
.. . .
0
1
2
2
2
012
1
3
111
1
1
0
0
1
3
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⇒===
(7.13)
Từ phương trình thứ tự áp ta có:
UUUU
NA NA NA N
... .
=++=
120
0
Và từ các phương trình cơ bản (7.1) ÷ (7.3) ta có:
EjIXXX
ANA
..
()
ΣΣΣΣ
−+
1120
0+ =
Như vậy: IE
jX X X
NA A
..
()
1
120
=++
Σ
ΣΣΣ
10
UjXIjXI U jXI I
UUUjIXX
N N NA NA NA NA
NA N NA NA
... . .
....
()(
000012
2221
1021
02
=− =− =−
=− + = +
ΣΣ Σ Σ
ΣΣ
; = -jX
)
.
Dòng tại chỗ ngắn mạch, cũng là dòng đi qua đất IĐ:
III
NA Â NA
...
==31
Ap tại chỗ ngắn mạch:
UUaUaU jaaX aXI
IXaX IX a
X
X
NB N NA NA NA
NA NA
.. . . .
..
[( ) ( ) ]
((
=+ + = − +−
=−= −
021222201
120 120
2
1
331
)
ΣΣ
ΣΣ Σ Σ
Σ
)
UUaUaU jaaXaXI
IXaX IX a
X
X
NC N NA NA NA
NA NA
.. . . .
..
[( ) ( ) ]
((
=+ + =− +−
=− − =− −
01
22220
1
12201220
2
1
331
)
ΣΣ
ΣΣ Σ Σ
Σ
)
Hình 7.11
VI.3. Ngắn mạch 2 pha chạm đất:
Xét ngắn mạch 2 pha B, C
chạm đất (hình 7.12). Điều kiện
ngắn mạch là:
I
U
U
NA
NB
NC
.
.
.
(7.14)
(7.15)
(7.16)
=
=
=
0
0
0
Thay vào phương trình thứ tự
áp:
Hình 7.12
U
U
U
aa
aa
U
UU U U
N
NA
NA
NA
NNANA NA
.
.
.
.
.. . .
0
1
2
2
2
012
1
3
111
1
1
0
0
1
3
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⇒= =
= (7.17)
Từ (7.14) ta có: II
II
NA NA NA N
... .
=++=
120
0
Và từ các phương trình cơ bản (7.1) ÷ (7.3) ta có:
jX I jX I
NA N
2200
ΣΣ
..
=