ĐIỀU KIỆN CÂN BẰNG KHỐI LƯỢNG CƠ CẤU PHẲNG
NHIỀU BẬC TỰ DO
ThS. ĐỖ TRỌNG PHÚ
Bộ môn Thiết kế Máy - Khoa Cơ khí
Trường Đại học Giao thông Vận tải
GS. TSKH NGUYỄN VĂN KHANG
Bộ môn Cơ học Ứng dụng - Khoa Cơ khí
Trường Đại học Bách khoa Hà Nội
Tóm tắt: Bài báo giới thiệu một phương pháp thiết lập các điều kiện cân bằng cho cơ
cấu phẳng nhiều bậc tự do. Phương pháp có ưu điểm là thích hợp với việc áp dụng các
chương trình tính toán số đang được sử dụng rộng rãi như MATLAB, MAPLE. Các điều kiện
cân bằng hoàn toàn lực quán tính và mô men quán tính của cơ cấu 8 khâu phẳng 3 bậc tự do
được trình bày trong một thí dụ áp dụng.
Summary: This paper presents a method for deriving the balancing conditions of planar
mechanics with multi - degree of freedom. The method has advantage of being suitable for the
applications of the widely accessible computer algebra systems such as MATLAB, MAPLE. In
the example, the conditions for complete shaking force and shaking moment balaning of a
planar eight-bar linkage with 3 degree of freedom are given. CT 2
I. ĐẶT VẤN ĐỀ
Để cân bằng khối lượng cơ cấu phẳng trước hết phải thiết lập được các điều kiện cân bằng.
Những điều kiện cân bằng đó sẽ được sử dụng để xác định kích thước và vị trí của các đối trọng
hoặc các khâu phụ thêm vào cơ cấu ban đầu để triệt tiêu lực quán tính và mô men quán tính sinh
ra bởi các khâu động. Các phương pháp cân bằng cho cơ cấu phẳng một bậc tự do đã được công
bố rộng rãi trong nhiều công trình nghiên cứu. Tuy nhiên, các nghiên cứu về cở sở lý thuyết cân
bằng cơ cấu phẳng nhiều bậc tự do vẫn còn hạn chế, chưa có nhiều công trình được công bố.
Trong bài báo này, chúng tôi giới thiệu một phương pháp thiết lập các điều kiện cân bằng
tổng quát cho cơ cấu phẳng nhiều bậc tự do với cấu trúc bất kỳ. Thuật toán này rất phù hợp với
các trình ứng dụng tính toán số hiện đang được sử dụng rộng rãi như MATLAB, MAPLE. Các
điều kiện cân bằng của cơ cấu 8 khâu phẳng 3 bậc tự do sẽ được trình bày trong một thí dụ áp
dụng với sự trợ giúp của hệ chương trình tính MAPLE.
II. ĐIỀU KIỆN CÂN BẰNG KHỐI LƯỢNG CƠ CẤU PHẲNG NHIỀU BẬC TỰ DO
Xét hệ nhiều vật phẳng gồm
p
khâu, dẫn động bằng các khớp quay. Để biểu diễn hệ, sử
dụng các hệ toạ độ suy rộng 12 p i i
q ,q ,...,q ; q
=
ϕ. Các toạ độ suy rộng này được gọi là toạ độ
suy rộng loại 1. Véctơ các toạ độ suy rộng loại 1 có dạng: T
12 p
q ,q ,...,q
⎡
⎤
=
⎣
⎦
q (2.1)
Để biểu diễn hệ, cũng có thể sử dụng các toạ độ suy rộng loại 2. Các toạ độ suy rộng loại 2
được chọn như sau:
() ()
(
)
(
)
(
)
iiii
12
ucos,usin,i=1,..,p=ϕ =ϕ (2.2)
Véctơ các toạ độ suy rộng loại 2 có dạng: 11
cos ,sin ,...,cos ,sin T
pp
⎡
⎤
=ϕϕ ϕϕ
⎣
⎦
u (2.3)
Khi đó vị trí khối tâm của các khâu có thể biểu diễn dưới dạng sau:
; (2.4)
*T *T
Si xi i xi i
x=e e+=+au ua *T *T
Si yi i yi i
y=e e+=+bu ub
Trong đó các véctơ i
gồm các phần tử không phụ thuộc vào véctơ toạ độ suy rộng u,
và là các hằng số. Tương tự như cách biểu diễn phương trình (2.4), các phương trình
liên kết của cơ cấu có thể viết dưới dạng ma trận:
i
,ab
i
*
x
ei
*
y
e
[
]
III
,=Du d D = D D (2.5)
Trong đó ma trận D gồm các phần tử là các tham số hình học của cơ cấu và không phụ
thuộc vào véctơ các toạ độ suy rộng u, và d là véctơ hằng. Nếu hệ có r phương trình liên kết, ký
hiệu , khi đó cỡ của các véctơ và ma trận lần lượt là: .
m = 2p r×m r×1
,Dd
Phân chia các phần tử của véctơ u thành hai nhóm: T
TT
⎤
=
⎦
uvw (2.6)
Với v là véctơ hàm các toạ độ suy rộng tối thiểu, (2.5) có thể viết lại dưới dạng:
CT 2
[]
III I II
⎡⎤
=
⇒+ =
⎢⎥
⎣⎦
v
DD d DvDwd
w (2.7)
Ma trận được chọn sao cho là ma trận vuông không suy biến, số phần tử của véctơ
chính là số phương trình biểu diễn liên kết hình học của cơ cấu. Cỡ của các véctơ và ma trận có
dạng:
II
Dw
()
()
()
()
r×1 II I
m-r ×1 r× m-r r×r
,, ,vwD D
Điều kiện cân bằng lực quán tính:
pp
*
ii ii
i=1 i=1
d
F = ma =0 mv =0
dt
−⇒
∑∑
rrr (2.8)
Do là điều kiện đủ, từ (2.8) có thể suy ra:
p
ii
i1
m
=
0
=
∑v (2.9)
Viết lại (2.9) dưới dạng: (2.10)
pp
iSi iSi
i=1 i=1
mx =0, my =0
∑∑
&&
Từ (2.5), do
[
]
III
D= D D ta có: III
=
+=Du D v D w d (2.11)
11
II I II II I
−−
=− ⇒ = −Dw d Dv w D d D Dv
(2.12)
Vì d là véctơ hằng số, đạo hàm (2.12) thu được: (2.13)
1
II I
−
=−wDD
&v
&
Với v là véctơ các toạ độ suy rộng dư loại 2 tối thiểu, phương trình (2.4) có thể viết lại dưới
dạng: (2.14)
T
*TT *TT
Si xi iI iII xi iI iII
x=e+ e
⎡⎤
⎡⎤
=+ +
⎢⎥
⎣⎦
⎣⎦
v
aa avaw
w
(2.15)
T
*TT *TT
Si yi iI iII yi iI iII
y=e+ e
⎡⎤
⎡⎤
=+ +
⎢⎥
⎣⎦
⎣⎦
v
bb bvbw
w
CT 2
,ab
với . Và việc phân chia các phần tử của các véctơ i
tương ứng với việc
phân chia véctơ u:
i = 1, 2,..., p i
[]
[
]
T
i iI iII i iI iII
,==aaa bbb
T
(2.16)
Trong đó các véctơ có các thành phần không phụ thuộc vào véctơ u.
iI iII iI iII
,,,aa bb
Thay (2.12) vào (2.14) và (2.16) ta thu được:
TT
Si xi i xi i
x=e e+=+
g
vv
g
; (2.17)
T
Si yi i yi i
y=e e+=+hv vh
T
Trong đó ta đặt:
*T1
xi xi iII II
e=e −
+aDd
; ;
*T1
yi yi iII II
e=e −
+bDd TTT1
i iI iII II I
−
=−
g
aaDD
, (2.18)
TTT1
i iI iII II I
−
=−hbbDD
Đạo hàm (2.17) ta thu được: T
Si i Si i
x,y==
T
g
v
&&&
hv
&
=
0
(2.19)
Thay (2.19) vào (2.10) ta có: (2.20)
pp
TT
ii ii
i1 i1
m0,m0
==
=
∑∑
gv hv
&&
Từ (2.20) thu được các điều kiện đủ cân bằng lực quán tính:
pp
TT
ii ii
i1 i1
m0,m
==
=
=
∑∑
gh
. Có
thể viết lại dưới dạng: (2.21)
pp
ii ii
i1 i1
m0,m
==
=
∑∑
gh0=
⎤
Điều kiện cân bằng mô men lực quán tính: (2.22)
()
p
iSiSi SiSi Sii
i=1
mxy-yx +I =0⎡ϕ
⎣⎦
∑&
&&
Viết lại phương trình (2.22):
()
pp
iSiSi SiSi Sii 1 2
i=1 i=1
mxy-yx + I =K+K 0
ϕ
=
∑∑
&
&& (2.23)
Trong đó: ;
()
p
1 i Si Si Si Si
i=1
K= m xy yx−
∑&&
p
2Si
i=1
K= I i
ϕ
∑& (2.24)
Thay (2.14), (2.15) và (2.19) vào (2.24) thu được: (2.25)
T
11
K=+vSv lv
&
T
1
&
i1
m
=
=−
∑hhg
()
p
TTT
1ixiiyii
i1
me e
=
=−
∑
lhg
Trong đó: Sg ; (2.26)
()
pTT
1iiii
i
Theo cách chọn (2.2), với chú ý rằng:
(
)
(
)
(
)
(
)
(
)
ii ii 22
i12 21 i i i
=u u u u cos sin
ϕ
−=ϕϕ+
&&
&& ϕ (2.27)
CT 2
i
i
Viết lại (2.27) dưới dạng ma trận:
() () ()
()
()
()
()
()
T
ii
ii
21 2
i12 ii
12 1
uu u
01
uu = 10
uu u
⎡
⎤⎡ ⎤ ⎡ ⎤
⎡⎤
⎡⎤
ϕ=
⎢
⎥⎢ ⎥ ⎢ ⎥
⎢⎥
⎣⎦ −
⎣⎦
⎢
⎥⎢ ⎥ ⎢ ⎥
⎣
⎦⎣ ⎦ ⎣ ⎦
&&
&
&&
(2.28)
Khi đó (2.24) có dạng: (2.29)
()
()
()
()
T
ii
pp Si12
T
2Sii ii
i=1 i=1 Si
21
0Iuu
K= I I0
uu
⎡⎤ ⎡⎤
⎡⎤
ϕ= =
⎢⎥ ⎢⎥
⎢⎥
−
⎢⎥⎣ ⎦⎢⎥
⎣⎦ ⎣⎦
∑∑ uHu
&
&&
&
Trong đó:
(2.30)
=
⎡⎤
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥
⎣⎦
1
1
m-r
m-r
m-r+1
m-r+1
m
mm×m
0I |
-I 0 |
... |
0I |
-I 0 |
H--- - -| - - -- -
|0I
|-I 0
| ...
|0
|-I
I
0
Chia H thành ma trận khối: 12
34
m×m
⎡
⎤
=
⎢
⎥
⎣
⎦
HH
HHH (2.31)
Trong đó: ma trận phản đối xứng cỡ
1:H
(
)
(
)
mr×mr
−
−
4:H ma trận phản đối xứng cỡ r×r
2:H ma trận không hình chữ nhật cỡ
(
)
mr×r−
3:H ma trận không hình chữ nhật cỡ
(
)
r× m r
−
Với chú ý rằng là các ma trận không. Khi đó có dạng:
2
,HH
3
TT
14
&&
T
2
&
2
K
T
T
1
T
2
T
4
K⎡⎤
⎡⎤
⎡⎤
== = +
⎢⎥
⎢⎥
⎢⎥
⎣⎦
⎣⎦
⎣⎦
H0v
v
uHu vHv wHw
0H w
w
&
&
& (2.32)
Thế (2.12) và (2.13) vào (2.32) ta có: (2.33)
T
22
K=+vSv lv
&
Trong đó:
(
)
(
)
T
11
2 1 II I 4 II I
−−
=+SH DDHDD
;
(
)
(
)
T
T1 1
2II4II
−−
=−lDdHDD
I
=
(2.34)
Viết lại (2.23): (2.35)
() ()
()
pp
TTT
iSiSi SiSi Sii 1 2 1 2
i=1 i=1
mxy yx + J = 0−ϕ+++
∑∑
vS Sv l lv
&
&& & &
Từ (2.35) ta thu được các điều kiện đủ để cân bằng mô men lực quán tính là:
12 12
0, 0
+
=+=SS ll (2.36)
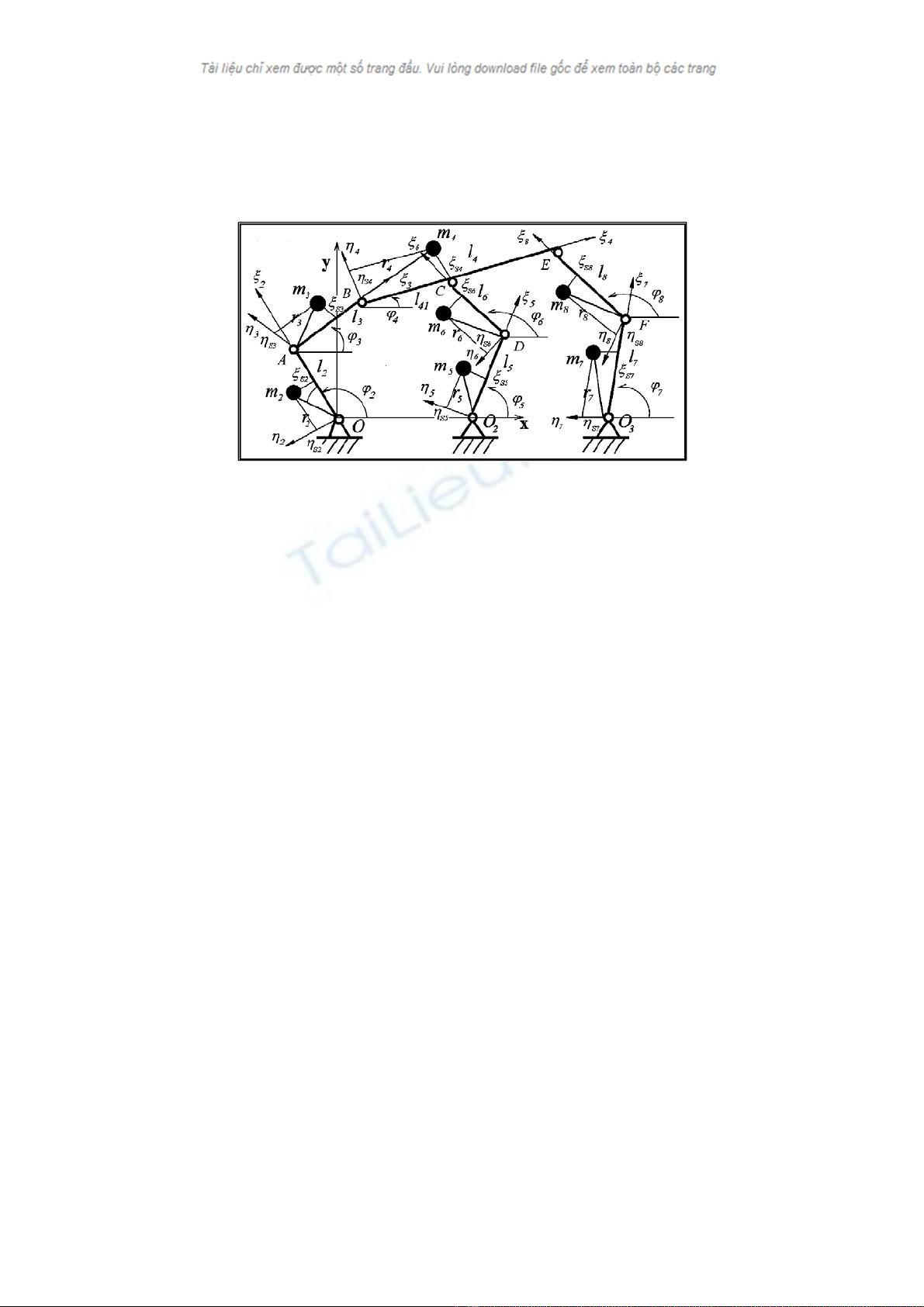
III. CÂN BẰNG KHỐI LƯỢNG CƠ CẤU 8 KHÂU PHẲNG 3 BẬC TỰ DO
Xét cơ cấu phẳng 3 bậc tự do gồm 8 khâu như hình 3.1.
Hình 3.1. Mô hình cơ cấu 8 khâu phẳng 3 bậc tự do
Hệ toạ độ cố định gắn chặt với nền, các hệ toạ độ Oxyz
(
)
iii
Oξη i=2,..,8 gắn chặt với các
khâu . Khối tâm của các khâu tương ứng là: ,
2
OA,AB,BE,CD,DO ,EF,FO3
()
2S2S2
Sξ,η
()
3S3S3
Sξ,η,
()
44
4S S
Sξ,η,
(
)
55
5S S
Sξ,η,
(
)
66
6S S
Sξ,η,
(
)
77
7S S
Sξ,η,
(
)
88
8S S
Sξ,η.
Các toạ độ suy rộng lần lượt là các góc quay:
2
34567
ϕ
,ϕ ,ϕ ,ϕ ,ϕ ,ϕ và
8
ϕ
.
Sử dụng các ký hiệu: là độ dài của khâu thứ
i
l
(
)
i i = 2,..,8 , trong đó và ;
toạ độ điểm
4
l=BE 41
l=BC
()
(
)
(
)
22 33
2O O 3O O
0,0 ,O x , y ,O x , y
1
Ο≡Ο ; là khối lượng của khâu thứ i; là mô
men quán tính khối tâm của khâu thứ i đối với trục đi qua khối tâm ; là ma trận cosin chỉ
hướng của khâu thứ i so với hệ toạ độ cố định : (3.1)
i
mi
I
i
Si
A
Oxyz
(
ii
i
ii
cos sin ,i=2,..,8
sin cos
ϕ− ϕ
⎡⎤
=⎢⎥
ϕϕ
⎣⎦
A
CT 2
)
6
8
Từ điều kiện ràng buộc của hai vòng kín độc lập và ,
ta có phương trình liên kết của cơ cấu 8 khâu 3 bậc tự do cho trên hình vẽ trên có dạng:
l=0
∑rr
2
OABCDO O 3
OABEFO O
2
2
3
3
2233414O556
2233414O5566
223344O778
223344O7788
l cos + l cos + l cos = x + l cos + l cos
l sin + l sin + l sin = y + l sin + l sin
l cos + l cos + l cos = x + l cos + l cos
l sin + l sin + l sin = y + l sin + l sin
ϕϕ ϕ ϕϕ
⎧
⎪ϕϕ ϕ ϕϕ
⎪
⎨
ϕϕϕ ϕϕ
⎪
⎪ϕϕϕ ϕϕ
⎩
(3.2)
Theo phương pháp véctơ các toạ độ suy rộng loại 2, căn cứ vào các ma trận cosin chỉ
hướng ta chọn véctơ u chứa các toạ độ suy rộng như sau:
(3.3)
[
]
2233 44 5
T
66 77 88
cos ,sin ,cos ,sin ,cos ,sin ,cos ,sin ,
cos ,sin ,cos ,sin ,cos ,sin
ϕ
=ϕϕ ϕ ϕϕ ϕϕ
ϕϕ ϕϕ ϕϕ
u5
Bốn phương trình liên kết (3.2) có thể biểu diễn dưới dạng ma trận như sau: