
CÁC ĐIỀU KIỆN CÂN BẰNG TĨNH CƠ CẤU SONG SONG
KHÔNG GIAN 4 BẬC TỰ DO
ThS. ĐỖ TRỌNG PHÚ
Bộ môn Thiết kế Máy - Khoa Cơ khí
Trường Đại học Giao thông Vận tải
GS. TSKH NGUYỄN VĂN KHANG
Bộ môn Cơ học Ứng dụng - Khoa Cơ khí
Trường Đại học Bách khoa
CT 2
I. MỞ ĐẦU
Cân bằng khối lượng của cơ cấu là các biện pháp làm giảm hoặc triệt tiêu véctơ lực quán
tính chính và véctơ mômen lực quán tính chính của các khâu động của cơ cấu. Bài toán cân
bằng khối lượng của các cơ cấu máy đã được nhiều nhà nghiên cứu quan tâm, nhiều công trình
nghiên cứu cân bằng khối lượng của cơ cấu được công bố trên nhiều tạp chí chuyên khảo.
Một đánh giá tổng quan các nghiên cứu về cân bằng khối lượng cơ cấu được trình bày
trong công trình [1, 2, 3, 6] và nhiều công trình khác. Các kết quả cân bằng lực quán tính các cơ
cấu chấp hành song song ba, bốn và sáu bậc tự do bằng cách thêm vào các khối lượng phụ trên
các khâu đã được đăng tải trong các công trình [4, 5].
Các tay máy song song không gian ngày càng có nhiều ứng dụng trong lĩnh vực cơ khí. Do
đó sự cân bằng khối lượng cơ cấu hoặc tay máy song song không gian trở thành một nhiệm vụ
quan trọng. Trong bài báo này thiết lập một dạng các điều kiện cân bằng của các cơ cấu không
gian dựa trên khái niệm véctơ hàm các toạ độ suy rộng dư [3].
II. CÁC ĐIỀU KIỆN CÂN BẰNG HỆ LỰC QUÁN TÍNH CỦA CƠ CẤU KHÔNG GIAN
Xét hệ nhiều vật không gian gồm p khâu, được dẫn động quay. Sử dụng các hệ toạ độ suy
rộng q1, q2, …, qq . Véctơ các toạ độ suy rộng có dạng: T
12 p
=q,q,...,q
⎡
⎤
⎣
⎦
q
Tóm tắt: Bài báo giới thiệu một phương pháp thiết lập các điều kiện cân bằng tĩnh cho
cơ cấu không gian nhiều bậc tự do. Phương pháp có ưu điểm là thích hợp với việc áp dụng
các chương trình tính toán số đang được sử dụng rộng rãi như Maple, Mathematica. Các điều
kiện cân bằng hoàn toàn lực quán tính của cơ cấu song song không gian 4 bậc tự do được
trình bày trong một thí dụ áp dụng.
Summary: This paper presents a method for deriving the static balancing conditions of
spatial mechanisms with multi - degree - of - freedom. The method has advantage of being
suitable for the applications of the widely accessible computer algebra systems such as Maple,
Mathematica. In the example, the static balancing conditions for complete shaking force of a
spatial four - degree - of - freedom parallel mechanism are given.
(2.1)
Biểu thức cân bằng lực quán tính theo [6]:
pp
*
ii ii
i=1 i=1
d
Fma0 mv
dt 0
=
−=⇒
∑∑
rrr=
p
i=1
(2.2)
Do là điều kiện đủ, từ (2.2) có thể suy ra: ii
m0
=
∑ (2.3)
v
Viết lại (2.3) dưới dạng: (2.4)
ppp
iSi iSi iSi
i=1 i=1 i=1
mx =0, my =0, mz =0
∑∑∑
&&&
Việc biểu diễn vị trí ( r), vận tốc ( ) của khối tâm của khâu thứ i của một cơ cấu
dưới dạng giải tích tường minh rất khó thực hiện. Để biến đổi các điều kiện cân bằng dạng vi
phân về dạng đại số, ta cần sử dụng số toạ độ suy rộng lớn hơn số bậc tự do của hệ.
i
Si
S
vi
S
Sử dụng ma trận côsin chỉ hướng để xác định vị trí khối tâm của khâu thứ i đối với hệ
toạ độ cố định theo hệ thức: rr (2.5) trong đó là véctơ toạ độ của điểm gốc
của hệ toạ độ động
{
i
S
()
ii
i
SO iS
=+Ar
ii
O
ri
O
}
iii
Oξηζ
i gắn liền với khâu thứ i đối với hệ toạ độ cố định
{
}
Oxyz và r
là véctơ toạ độ của điểm trên hệ toạ độ
động
()
i
i
S
i
S
{
}
iiii
Oξηζ
iii
SSS
ξη
⎡
⎣
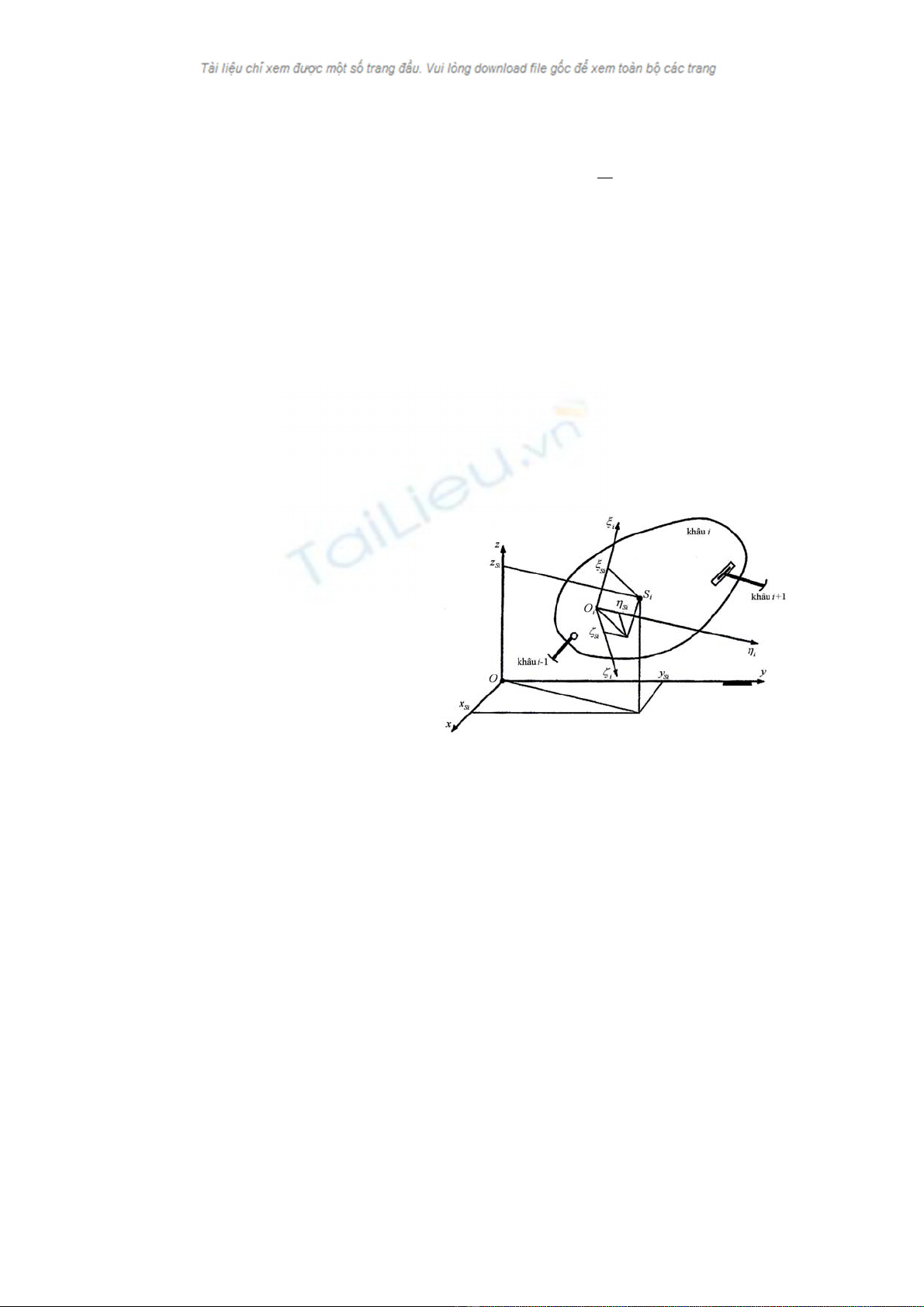
như trên hình 2.1. là
ma trận cosin chỉ hướng của khâu thứ i:
(2.6)
i
A
()
i=ζri
T
S
⎤
⎦
Chọn một véctơ hàm các toạ độ suy
rộng dư bao gồm
các phần tử là hàm của các toạ độ suy rộng
dư, sao cho vị trí của khối tâm có thể
biểu diễn dưới dạng: Hình 2.1. Định nghĩa hệ trục toạ độ không gian
[]
T
12 m
z z ... z=z
i
S
CT 2
(2.7)
iii
*T *T *T
Sxii Syii Szii
x = e + , y = e , z = e , i = 1,2,...,p++az bz cz
Véctơ có các thành phần không phụ thuộc vào toạ độ suy rộng , các thành phần
của véctơ là các hàm của các toạ độ suy rộng, và là hằng số.
iii
,,abc
z
q
**
yi
e,e
xi
*
zi
e
Tương tự như cách biểu diễn phương trình (2.7), các phương trình liên kết của cơ cấu có
thể viết dưới dạng ma trận:
[
]
=,
*
III
Dz + f 0 D = D D (2.8)
Các ma trận D và f chỉ gồm các phần tử là các tham số hình học của cơ cấu và không phụ
thuộc vào toạ độ suy rộng . Phân véctơ z thành hai nhóm:
*
q
[
]
T
z= v w (2.9) với v là véctơ
hàm các toạ độ suy rộng tối thiểu, (2.7) có thể viết lại dưới dạng:
(2.10)
ii i
*T T *T T *T T
SxiiI iII SxiiI iIISxiiI iII
x = e + , y = e , z = e , i = 1,2,...,p+++++av aw bv b w cv cw
Trong đó:
[
]
[
]
[
]
TT
i iI iII i iI iII i iI iII
,,===aaa bbb ccc
T
(2.11)

Phương trình liên kết (2.8) có thể viết lại dưới dạng: III
*0
+
+Dv D w
M
=f (2.12)
a trận được chọn sao cho là ma trận vuông không suy biến, số phần tử của véctơ
chín
II
D
ươ
w
tơh là số ph ng trình biểu diễn liên kết hình học của cơ cấu. Từ (2.12) có thể biểu diễn véc
wqua véctơ v như sau:
(
)
1*
II I
−
=− +wDfDv (2.13)
Thế (2.13) vào (2.10) ta được: T
+
(2.14)
Từ đó suy ra:
iii
TT
Sxii Syii Szii
x=e ,y=e ,z=e++gv hv kv
()
i
TTT
Si S i 12 n
, , q ,q ,...,q
ii
Si,∂∂
′′′
====
∂∂∂
vv
xg yh zk q
qqq (2.15)
Trong đó và có dạng:
−
−
−
(2.16)
Thế phương trình (2.15) vào các điều kiện cân bằng (2.4) thu được:
∂v
ii
,gh i
k
T T T1 T T T1 T T T1
i iI iII II I i iI iII II I i iI iII II I
* T 1* * T 1* * T 1*
xi xi iII II yi yi iII II zi zi iII II
,,
e=e , e=e , e=e
−−
−−
=− =− =−
−−
gaaDDhbbDDkccDD
aDf bDf cDf
pp p
TT T
ii ii i i
i=1 i=1 i=1
m0,m0,m
⎛⎞⎛⎞ ⎛⎞
∂∂ 0
∂
=
==
⎜⎟⎜⎟ ⎜⎟
∂∂
⎝⎠⎝⎠ ⎝⎠
∑∑∑
vv
gh k
qq∂
v
q
(2.17)
Để cho điều kiện (2.17) được thoả mãn với mọi giá trị của v
T
k
(2.18)
Các phương trình (2.18) chính là các điều kiện cân bằng lực quán tính của cơ cấu dưới
dạng
III. CÂN BẰNG CƠ CẤU SONG SONG KHÔNG GIAN BỐN BẬC TỰ DO
ơ cấu gồm 5
chân
i tâm của mỗi khâu, trên mỗi khâu định nghĩa một toạ độ tham chiếu. Hệ
trục
thì:
TT
ii ii i i
i=1 i=1 i=1
m = 0, m = 0, m = 0
∑∑∑
gh
ppp
CT 2
đại số. Việc dẫn ra các phần tử của i
g, i
h và i
k là tương đối phức tạp về mặt toán học,
thí dụ trong mục 3 sẽ cho thấy phương phá nà rất phù hợp với hệ chương trình như Maple. p y
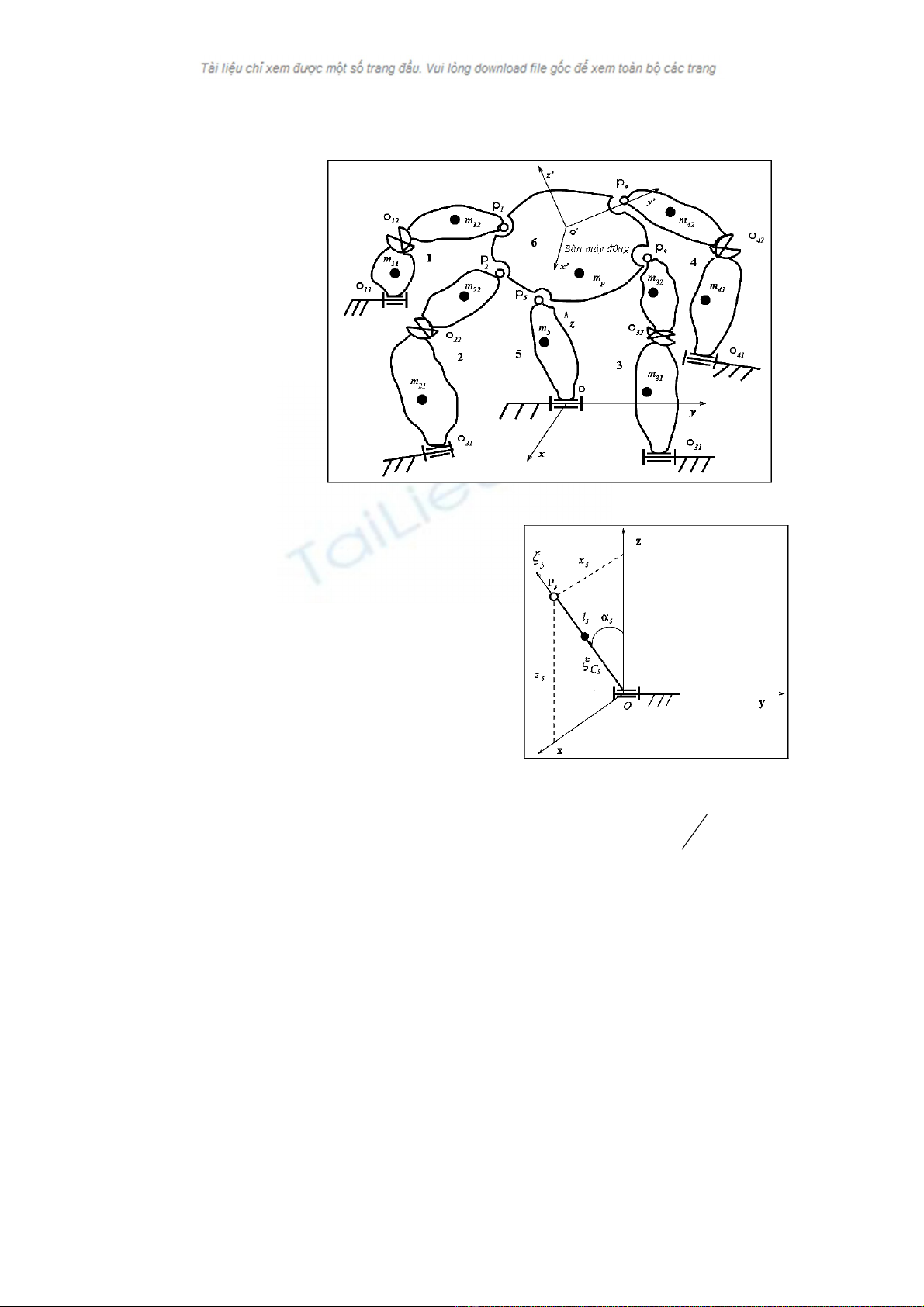
Xét cơ cấu song song không gian 4 bậc tự do dẫn động quay như hình 3.1. C
liên kết bệ máy với bàn máy động, trong đó 4 chân được dẫn động. Mỗi chân nối với bàn
máy cố định bằng một khớp bản lề và nối với bàn máy động bằng một khớp cầu. Chân 5 không
được dẫn động và chỉ gồm một khâu, bốn chân được dẫn động đều gồm có 2 khâu, nối với nhau
bằng khớp các - đăng.
Để mô tả vị trí khố
toạ độ cố định Oxyz với trục z hướng lên trên và gốc toạ độ O được đặt tại tâm của khớp
bản lề của chân thứ 5 n trên hình .2. Hệ toạ độ di động Oxyz
hư 3
′
′′′ ược gán với bàn máy động
tại điểm O′ thuộc bàn máy động.
Toạ đề - các của bàn máy
đ
độ động được xác định qua vị trí của gốc O' so với hệ toạ độ cố
định Oxyz và được ký hiệu là
[
]
T
x, y,z=p, hướng của bàn máy động (hướng của hệ toạ độ
động z
′′
với hệ toạ
độ cố định) đh
qua ma trận quay Q. Các
phần tử của ma trận quay
là các ủa các góc
Euler, các bất biến bậc
hai, bất biến tuyến tính
hoặc các thành phần
khác.
Toạ độ các điểm nối
i
P trong hệ toạ độ động
của bàn máy động được
ký hiệu là
(
O x y
′′
ư
hàm c
ợc xác địn
)
iii
a,b,c với
CT 2
i
=1,..,5. Khi đó: H h 3.1. Sơ đồ cơ cấu song song không gian 4 bậc tự do dẫn động quay
)
5
, i 1,..,4
′=
pQ (3.1)
trong đó p là
ìn
ểm trong hệ toạ
độ c
(
i
′
p
ctơ v
,
i5
=+
p
i
định Ox
−
p
vé ị trí của các đi
ốyz i
i
P
′
p
củ
h 3.
ơ vị
là véctơ vị trí
Véct ệ toạ độ cố định
như
ứ 5 nằm trên đường nối giữ và , khi đó có
thể trí khối tâm
của các điểm i
P
trong hệ to độ động O x y z
′′′′
:
[][]
T
iiii i ii
xyz , abc
==pp
(3.2)
ạ
5
p là vị
mô tả trên hìn
=
xác định véct
T
i
′
ơ trí a điểm 5
P trong h
2, được xác định theo:
[]
T
55 5
lcosα0lcosp (3.3)
Giả thiết rằng vị trí khối tâm của chân th
α
a O5
P
H
ình 3.2. Hệ toạ độ gắn với chân thứ 5
5c
55
l
l
⎛⎞
=⎜⎟
rp (3.4
của chân thứ 5 theo hình 2 như sau:
5
⎝
Trong đó 5
r là véctơ vị trí khối tâm, 5
l là chiều dài của chân và ài từO tới
⎠)
là chiều d
khố ủa chân thứ i củ cấu được mô tả như hình 3.3, hai hệ toạ độ am
chiế
5c
l
t
i tâm 5
S .
ạ
âu thứ 2
Hai khâu c a cơ
n
th
thu i1 i1 i1
Oξηζ và i2 i2 i2 i2
Oξηζ lần lượt gắ với khâu động thứ nhất và hứ hai của chân ứ i.
Hai gốc to độ i1
O và i2
O lần lượt được đặt tại tâm của hai khớp. Giả thiết rằng khối tâm i2
C
của kh thuộc chân th i (i=1 ,.., 4) nằm trên đường nối i2
O và i
P. Như hình 3.3, sử
dụng các ký hiệu i2 i i2 i2 i2
l=OP,ξ=O C và gọi i
Ci2i
l=CP hay ii2
Ci2C
l=l ξ
i1
ứ
i2
−
.
Các toạ độ củ toạ độ ới bàn ng,
(
ác điểm trong hệđộng gắn v máy di độ được ký hiệu là
i
Pa c
)
, và h ng của hệ toạ độ độngướ O x y z
′
′′′
iii
,c với ia,b 1,..,4= đối với hệ toạ độ cố định Oxyz

CT 2
đượcy
được đặt t của kh
với
ủa trụcủa hệ toạ độ cố định với trục
mô tả bằng ma trận qua Q. Điểm i1
O
ại tâm ớp bản lề của chân thứ
i. Toạ độ của điểm i1
O biểu diễn rong hệ to
độ cố định là
()
T
i0 i0 i0
x,y,z , với i 1,...,4=.
Ta cũng dùng ký hiệu i1
C và ượt
là vị trí khối t hâu d
t
ướ
iữ
ạ
ối
i2
C lần l
i (khâu n
(k
i
âm c a kủa củ
bàn máy cố định) và kh trên hâu nối
với bàn máy động) của chân thứ i. Gọi i1
θ và
i2
θ lần lượt là các góc giữa khâu động thứ
nhất và khâu động thứ hai của chân thứvới
c z của hệ toạ độ cố định, i
γ là góc giữa
hướng dương của trục x của hệ toạ độ cố
định với trục i1
ζ, và i
β là góc g a hướng dương c
âu
trụ
c x 2i
ξ
Hình 3.3. Hệ toạ độ gắn với chân thứ i
,
t
ó,
trong đó giả thiết rằng véc tơ i1
ζ nằm trong mặ
ký hiệu đ có thể ết các ma trận cosin chỉ hướng:
ii1 i i1 i
i1 i i1 i i1 i
sinγsinθsi cosθcosγ
cosγsinθcosγcosθsinγ,
−
⎡⎤
⎢⎥
=−
⎢⎥
Q
i2 i i2 i
i2 i i2 i
co sinθcosβcosθsinβ
sinβsinθsinβcos
−
phẳng xy của hệ trục toạ độ cố định. Với các
vi
i1
sθ
i1
γ
sinθ
n
co 0
⎢⎥
⎣⎦
i
i2 i
i2 i2
sβ
θcosβ
cosθsinθ0
⎡
⎤
⎢
⎥
Q=
⎢
⎥
⎢
⎥
−
⎣
⎦
(3.5)
iả thi i tâm c hai của chân thứ i nằm trên đường thẳn
như mô tả đ
Đã g g nối OP ết rằ ố
trên hìn 3. Khi
ng, kh
h 3.
ủ
ó có th
a khâu th
ể viế
ứ
t: i1
i2 i
i 0 i1 i1 ,i 1,..,4
=
+=prQl
định
Oừ On
(3.7)
ừà khoảng cách từ ớ
trí củđượ công thức:
(3.6)
Trong đó i1
p và i0
r lần lượt là véctơ vị trí của các điểm 2
O,O đối với hệ toạ độ cố
(hình 3.3), lvà llần lượt là véctơ từ O t ro g hệ toạ độ khâu.
i1 i
tới i
P t
i1 i2
ách t
điểm ũng
i1
i1
i1
i1
zz
⎢
⎣
ới i2
O,
đị
ới
⎥
⎥
⎥
⎦
i2
l l
nh theo
i2 và t i2
i0
i0 i0 i1 i1 i2
xxll
y , y , , , i 1,..., 4
⎡⎤ ⎡⎤ ⎡⎤ ⎡⎤
⎢⎥ ⎢ ⎥ ⎥
====
⎢⎥ ⎢ ⎥ ⎥
rpll
c
i
Pc
i1 i2
i0
0 0
00
⎢ ⎢ =
⎢ ⎢
⎢⎥ ⎢⎥ ⎢⎥
⎣⎦ ⎣⎦ ⎣⎦
Với l là khoảng P i 1,...,4
=). Véctơ vị
i1
a các
i1
O t
c xác
i2
Oti i
ii
(
i
p
′
=
+ppQp
(3.8)
Trong đó :
[
]
[
]
TT
iiii
x y z , a b c , i 1,...,4
′
===
pp (3.9)
Véctơ vị ủ , của khâu thứ nhất và của khâu thứ hai
của:
trí i tâm c
nh qu
khố
đị
a bàn máy
=+rp
động
PP
Qc ;
P
r
i1
i1
a chân thứ i xác
r
i2
ri0 i1 i1
=
+Qbrr ; i2 i0 i1 i1 i2 i2
=
++rrQ Qbl (3.10)
Trong đó : Pi1i2
,,cbb lần lượt là véctơ vị trí hối tâm của bàn máy động, của khâu thứ nhất
thứ hai của chân thứ i xác địnoạ độ
k
và gắn liền với khâu. h trong hệ t

























![Giáo trình Solidworks nâng cao: Phần nâng cao [Full]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260128/cristianoronaldo02/135x160/62821769594561.jpg)
