Ti u lu n: Xác su t – Th ng kê ể ậ ấ ố GVHD: Tr n Chi nầ ế
KHOA: KHOA H C C B NỌ Ơ Ả
TI U LU NỂ Ậ
XÁC SU T TH NG KÊẤ Ố
Đ TÀI:Ề
Đ NH LÝ GI I H N TRUNG TÂM – CÁC X P X XÁC SU TỊ Ớ Ạ Ấ Ỉ Ấ
VÀ BÀI T PẬ
GVHD: Tr n Chi n ầ ế
L p: 211301101ớ
Khoa: K Toán – Ki m Toánế ể
Nhóm 1:
1. Nguy n Ng c Th nh (08106071ễ ọ ị )
2. Bùi Văn Ti p (08267261)ệ
3. Ph m Văn Toàn (08096701)ạ
4. Nguy n Nh Tuân (08251411)ễ ư
Thành ph H Chí Minh, 11/2009ố ồ
L p: ớ211301101 Tr ng Đ i h c Công Nghi p Thành ph H Chí Minhườ ạ ọ ệ ố ồ
Ti u lu n: Xác su t – Th ng kê ể ậ ấ ố GVHD: Tr n Chi nầ ế
KHOA: KHOA H C C B NỌ Ơ Ả
TI U LU NỂ Ậ
XÁC SU T TH NG KÊẤ Ố
Đ TÀI:Ề
Đ NH LÝ GI I H N TRUNG TÂM – CÁC X P X XÁC SU TỊ Ớ Ạ Ấ Ỉ Ấ
VÀ BÀI T PẬ
GVHD: Tr n Chi n ầ ế
L p: 211301101ớ
Khoa: K Toán – Ki m Toánế ể
Nhóm 1:
1. Nguy n Ng c Th nh (08106071)ễ ọ ị
2. Bùi Văn Ti p (08267261)ệ
3. Ph m Văn Toàn (08096701)ạ
4. Nguy n Nh Tuân (08251411)ễ ư
Thành ph H Chí Minh, 11/2009ố ồ
L p: ớ211301101 Tr ng Đ i h c Công Nghi p Thành ph H Chí Minhườ ạ ọ ệ ố ồ
Ti u lu n: Xác su t – Th ng kê ể ậ ấ ố GVHD: Tr n Chi nầ ế
PH N I: LÝ THUY TẦ Ế
Bài 3: Đ nh lý gi i h n trung tâm – các x p x xác su tị ớ ạ ấ ỉ ấ
3.1. Phân ph i liên t c: Phân ph i đ u và phân ph i chu nố ụ ố ề ố ẩ
3.1.1. Phân ph i đ u:ố ề
•Đ nh nghĩa:ị Bi n ng u nhiên X đ c g i là bi n ng u nhiên có phân ph i đ uế ẫ ượ ọ ế ẫ ố ề
trên đo n [a,b] n u có hàm m t đ là: ạ ế ậ ộ
•Hàm phân ph i xác su t:ố ấ Hàm phân ph i xác su t c a bi n ng u nhiên có phânố ấ ủ ế ẫ
ph i đ u là:ố ề
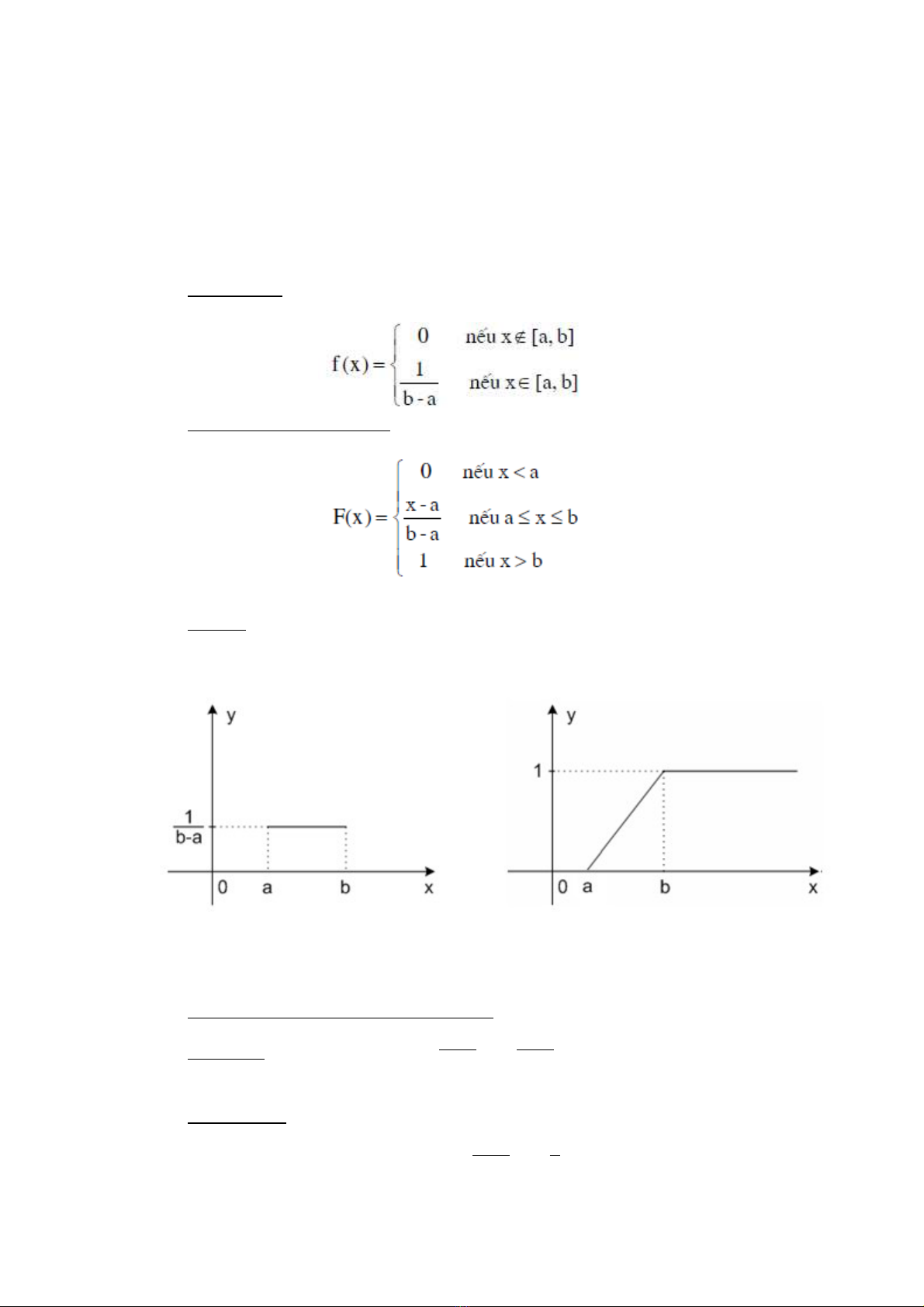
•Đ th :ồ ị Ta xét đ th c a hàm m t đ và hàm phân ph i xác su t c a phânồ ị ủ ậ ộ ố ấ ủ
ph i đ u trên [a,b] là:ố ề
Hình 1: Đ th hàm m t đ Hình 2: Đ th hàm phân ph i xác su tồ ị ậ ộ ồ ị ố ấ
c a phân ph i đ u.ủ ố ề c a phân ph i đ u.ủ ố ề
•Các đ c tr ng s c a phân ph i đ u:ặ ư ố ủ ố ề
Kỳ v ng:ọ
( ) ( ) ( )
2
b
a
x a b
E X xf x dx dx Med X
b a
+∞
−∞
+
= = = =
−
∫ ∫
Ph ng sai:ươ D(X) = E(X2) – E2(X)
V i: E(Xớ2) =
2
2 2 2
1
( ) ( )
3
b
a
x
x f x dx dx b ab a
b a
+∞
−∞
= = + +
−
∫ ∫
L p: ớ211301101 Tr ng Đ i h c Công Nghi p Thành ph H Chí Minhườ ạ ọ ệ ố ồ
Ti u lu n: Xác su t – Th ng kê ể ậ ấ ố GVHD: Tr n Chi nầ ế
( ) ( ) 2
b
a
x a b
E X xf x dx dx
b a
+∞
−∞
+
= = =
−
∫ ∫
(Tính trên)ở
Suy ra ph ng sai: D(X) = E(Xươ 2) – E2(X)
=
2 2
1( )
3b ab a+ +
- (
2
a b+
)2 =
2
( )
12
b a−
3.1.2. Phân ph i chu n:ố ẩ
•Đ nh nghĩa:ị Bi n ng u nhiên X đ c g i là bi n ng u nhiên có phân ph iế ẫ ượ ọ ế ẫ ố
chu n v i hai tham s µ và σẩ ớ ố 2 n u có hàm m t đ là: ế ậ ộ
f(x)=
2
2
( )
2
1
2
x
e
µ
σ
σ π
−
−
Kí hi u: X ~ N(µ;σệ2)
•Hàm phân ph i xác su t:ố ấ Phân ph i chu n có hàm phân ph i xác su t là: ố ẩ ố ấ
F(X)=
2
2
( )
2
1
2
t
x
e dt
µ
σ
σ π
−
−
−∞
∫
Do hàm m t đ c a phân ph i chu n không có nguyên hàm s c p nên taậ ộ ủ ố ẩ ơ ấ
không th bi u di n hàm phân ph i xác su t F(X) b i m t hàm s s c p.ể ể ễ ố ấ ở ộ ố ơ ấ
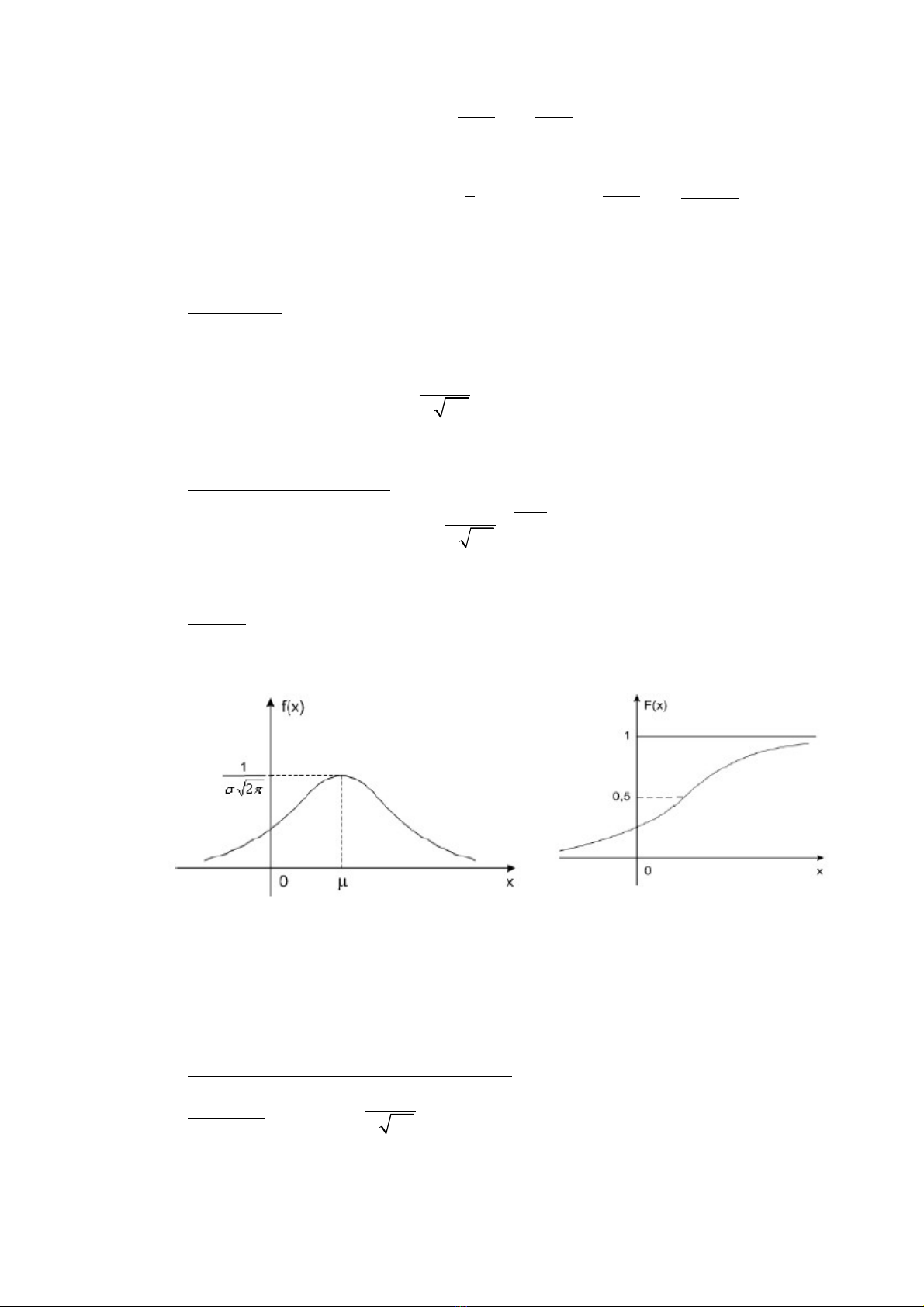
•Đ th :ồ ị Ta xét đ th c a hàm m t đ và hàm phân ph i xác su t c a phânồ ị ủ ậ ộ ố ấ ủ
ph i chu n nh sau:ố ẩ ư
Hình 3: Đ th hàm m t đ c aồ ị ậ ộ ủ Hình 4: Đ th hàm phân ph i xácồ ị ố
phân ph i chu n.ố ẩ su t c a phân ph iấ ủ ố
chu n.ẩ
Đ th hàm m t đ c a phân ph i chu n có d ng hình chuông nên phânồ ị ậ ộ ủ ố ẩ ạ
ph i chu n còn có tên g i là phân ph i hình chuông. ố ẩ ọ ố
•Các đ c tr ng s c a phân ph i chu n:ặ ư ố ủ ố ẩ
Kỳ v ng:ọ E(X) =
=
µ
Ph ng sai:ươ D(X) = E(X2) – E2(X)
L p: ớ211301101 Tr ng Đ i h c Công Nghi p Thành ph H Chí Minhườ ạ ọ ệ ố ồ
Ti u lu n: Xác su t – Th ng kê ể ậ ấ ố GVHD: Tr n Chi nầ ế
V i: E(Xớ2) =
2
2
( )
22
1
.2
x
x e dx
µ
σ
σ π
−
+∞ −
−∞
∫
= µ2 + σ2
E2(X) =
µ
2
Suy ra: D(X) = E(X2) – E2(X) = µ2 + σ2 –
µ
2 = σ2
V y ph ng saiậ ươ : D(X) = σ2
Ta th y hai tham s ấ ố
µ
và σ2 chính là kì v ng và ph ng sai c a phân ph iọ ươ ủ ố
chu n. T i đây ta có th kh ng đ nh phân ph i chu n hoàn toàn xác đ nh khiẩ ớ ể ẳ ị ố ẩ ị
bi t kì v ng và ph ng sai c a nó.ế ọ ươ ủ
•Tính xác su t:ấ Gi s X ~ N(ả ử
µ
;σ2)
P[a≤ X ≤b] =
2
2
( )
2
1
2
x
b
a
e dx
µ
σ
σ π
−
−
∫
=
( ) ( )
b a
µ µ
φ φ
σ σ
− −
−
•Quy t c ắ 3
σ
: Xét bi n ng u nhiên X v i kì v ng ế ẫ ớ ọ
µ
và ph ng sai σươ 2
[ ] 2 ( ) 1
X
P X P
µ ε ε
µ ε φ
σ σ σ
−
− < = < = −
V i ớ
ε σ
=
ta có:
[ ]=2 (1) - 1 = 0,6826P X
µ σ φ
− <
V i ớ
2
ε σ
=
ta có:
[ 2 ]=2 (2) - 1 = 0,9544P X
µ σ φ
− <
V i ớ
3
ε σ
=
ta có:
[ 3 ]=2 (3) - 1 = 0,9973P X
µ σ φ
− <
Nh v y n u X ~ N((ư ậ ế
µ
;σ2) thì
[ ] 1P X
µ ε
− < =
khi
3
ε σ
>
. Đi u này cóề
nghĩa là n u bi n ng u nhiên X có phân ph i chu n v i kì v ng µ và ph ngế ế ẫ ố ẩ ớ ọ ươ
sai σ2 thì g n nh ch c ch n r ng X s nh n giá tr trong kho ng [ầ ư ắ ắ ằ ẽ ậ ị ả
µ
- 3σ ,
µ
+
3σ]
•B sung v ki n th c phân ph i chu n t c: ổ ề ế ứ ố ẩ ắ N u bi n ng u nhiên X cóế ế ẫ
phân ph i v i kì v ng µ = 0 và ph ng sai ố ớ ọ ươ σ2 = 1 thì X đ c g i là bi n ng uượ ọ ế ẫ
nhiên có phân ph i chu n t c ho c phân ph i Gauss. Hàm m t đ c a phânố ẩ ắ ặ ố ậ ộ ủ
ph i chu n t c đ c kí hi u là ố ẩ ắ ượ ệ
( )x
ϕ
còn g i là hàm Gauss, hàm phân ph iọ ố
đ c kí hi u là ượ ệ
( )x
φ
còn g i là hàm Laplace.ọ
- Hàm
( )x
ϕ
là hàm ch n, ẵ
( ) ( )x x
ϕ ϕ
− =
, trong kho ng (0, +∞) thì hàm ả
( )x
ϕ
đ nơ
đi u gi m. ệ ả
(0) 0,3989
ϕ
=
,
(1) 0,2420
ϕ
=
,
(2) 0,0540
ϕ
=
,
(3) 0,0044
ϕ
=
,
(4) 0,0001
ϕ
=
và n u x≥4 thì ế
( )x
ϕ
0
≈
- Hàm
( )x
φ
=
( )
x
t dt
ϕ
−∞
∫
Hàm
( )x
φ
là hàm l .ẻ
Ta có:
(0) 0,5
φ
=
,
(1) 0,2420
φ
=
,
(2) 0,0540
φ
=
,
(3) 0,0044
φ
=
,
(3,9) 0,0001
φ
=
và
n u x≥4 thì ế
( ) 1x
φ
≈
và n u x < -4 thì ế
( ) 0x
φ
≈
L p: ớ211301101 Tr ng Đ i h c Công Nghi p Thành ph H Chí Minhườ ạ ọ ệ ố ồ