CÂU 2 CH NG 3ƯƠ
Đ bài :ềXác đ nh đ th Bode c a hàm truy n đ tị ồ ị ủ ề ạ
đi n áp sau:ệ
F(p)=
2
1
( )
( )
U p
U P
Trong đó R1=80 k
Ω
R2=20 k
Ω
,L=1mH
ZL=j L=PL
Zc= =
L i gi i:ờ ả
F(p)=
2
1
( )
( )
U p
U P
=
2 1
1 2 1
/ / ( )
( / / ) ( )
R PL U p
R R PL U P+
=
2
1 2
/ /
( / / )
R PL
R R PL
+
=
2
2
2
1
2
R PL
R PL
R PL
RR PL
+
++
=
2
1 2 1 2
( )
R PL
R R R L R L P
+ +
=
=
K=
2
1 2
R L
R R
=
3 3
6
20.10 .10
80.20.10
−
=1,25.10-8
P10=0
1 2
1
1 2
R R
PR L R L
∞
= − +
=-16 .106
F(P)=k F(j )=k+j0
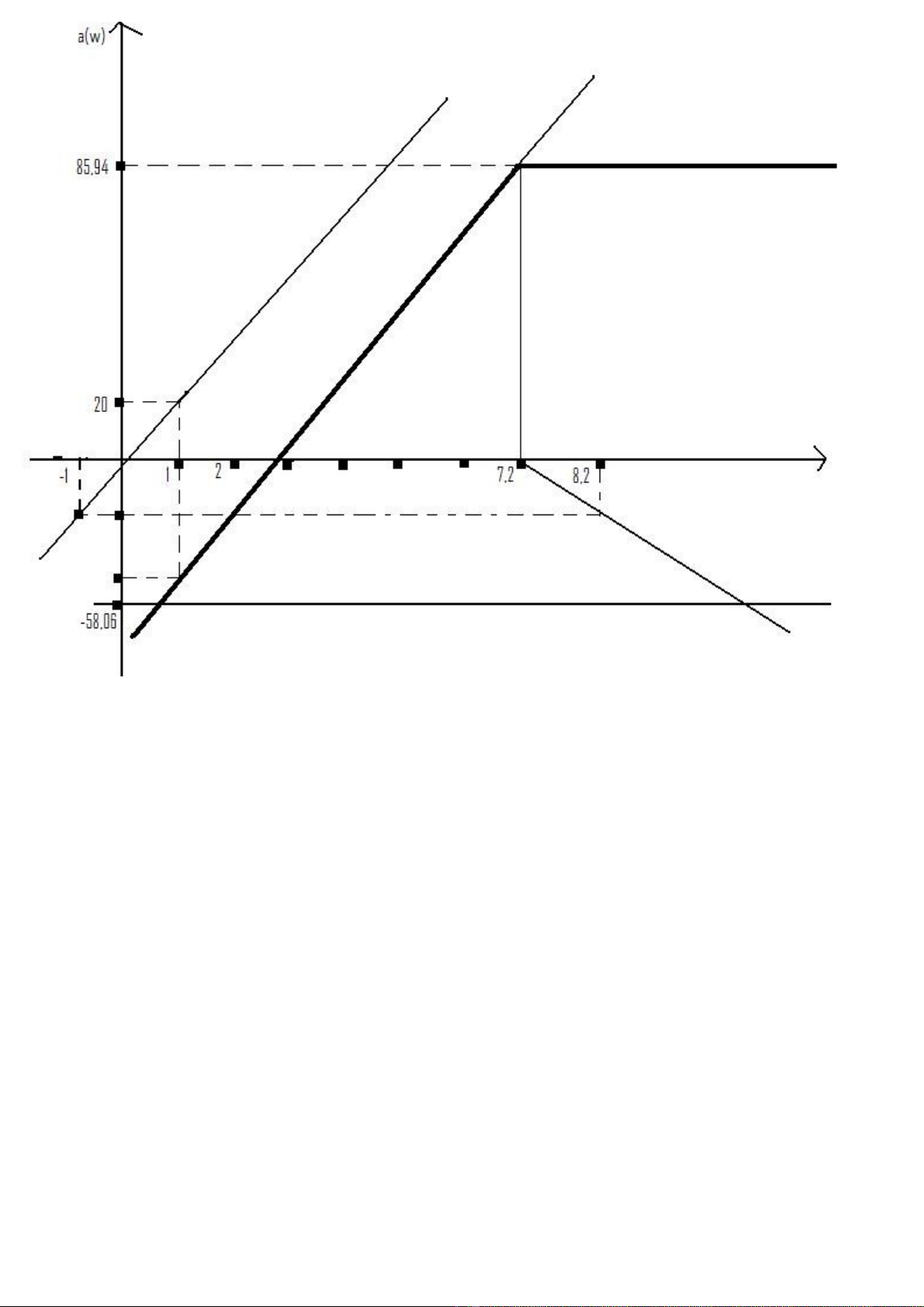
a( )=20lg| F(j |=20lg|k|=-58,06
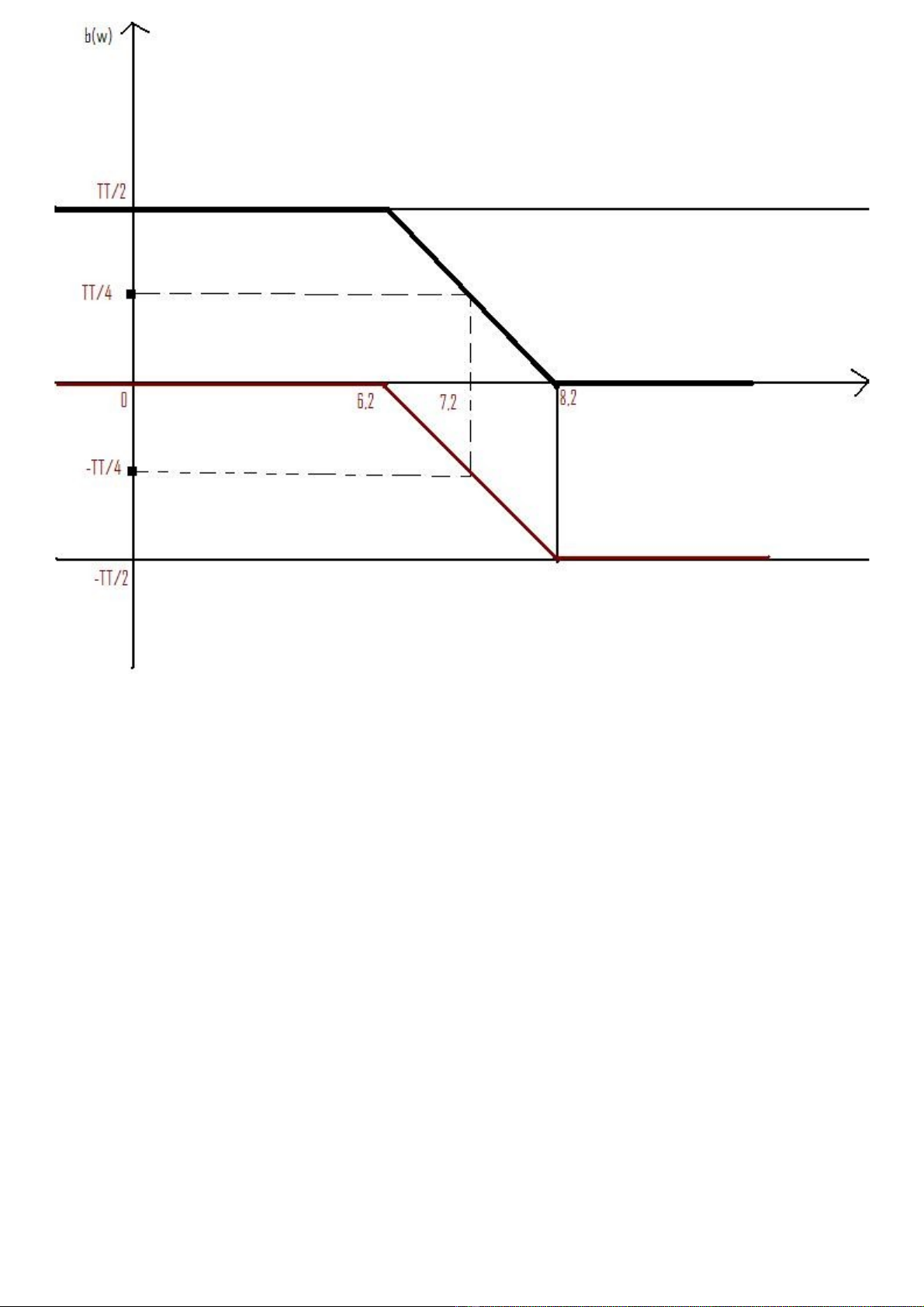
b( =0 (k>0)
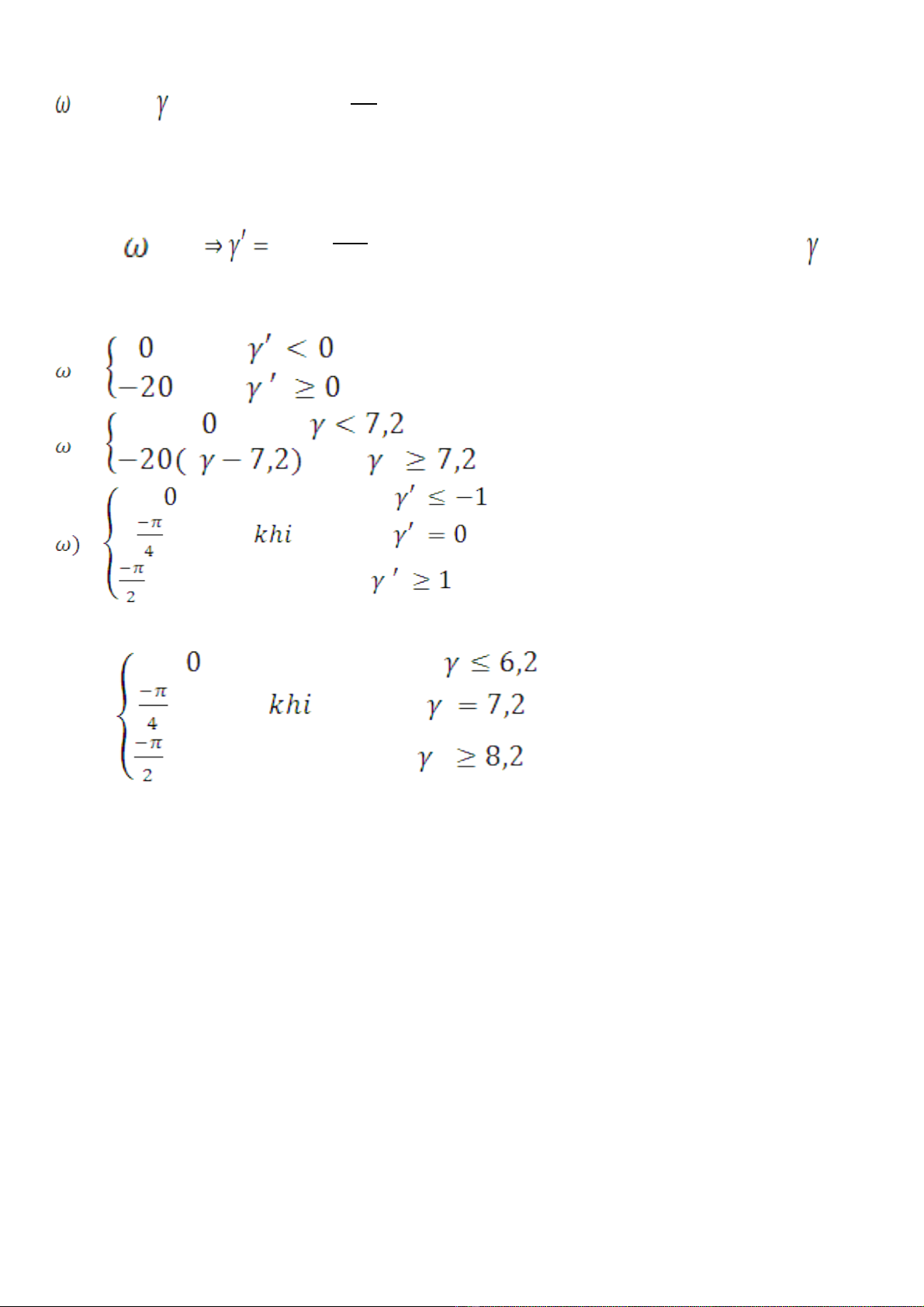
P(i0)=0
a( )=20 ,
( ) 2
b
ω
Π
=
6
1
16.10
h
P
ω
∞
= − = −
Ch n ọ0=1
6
lg lg lg lg lg(16.10 )
h
h
ωω ω ω
ω
= − = − =
-7,2
a( )=
a( )=
b( =
=
CÂU 5 CH NG 4ƯƠ
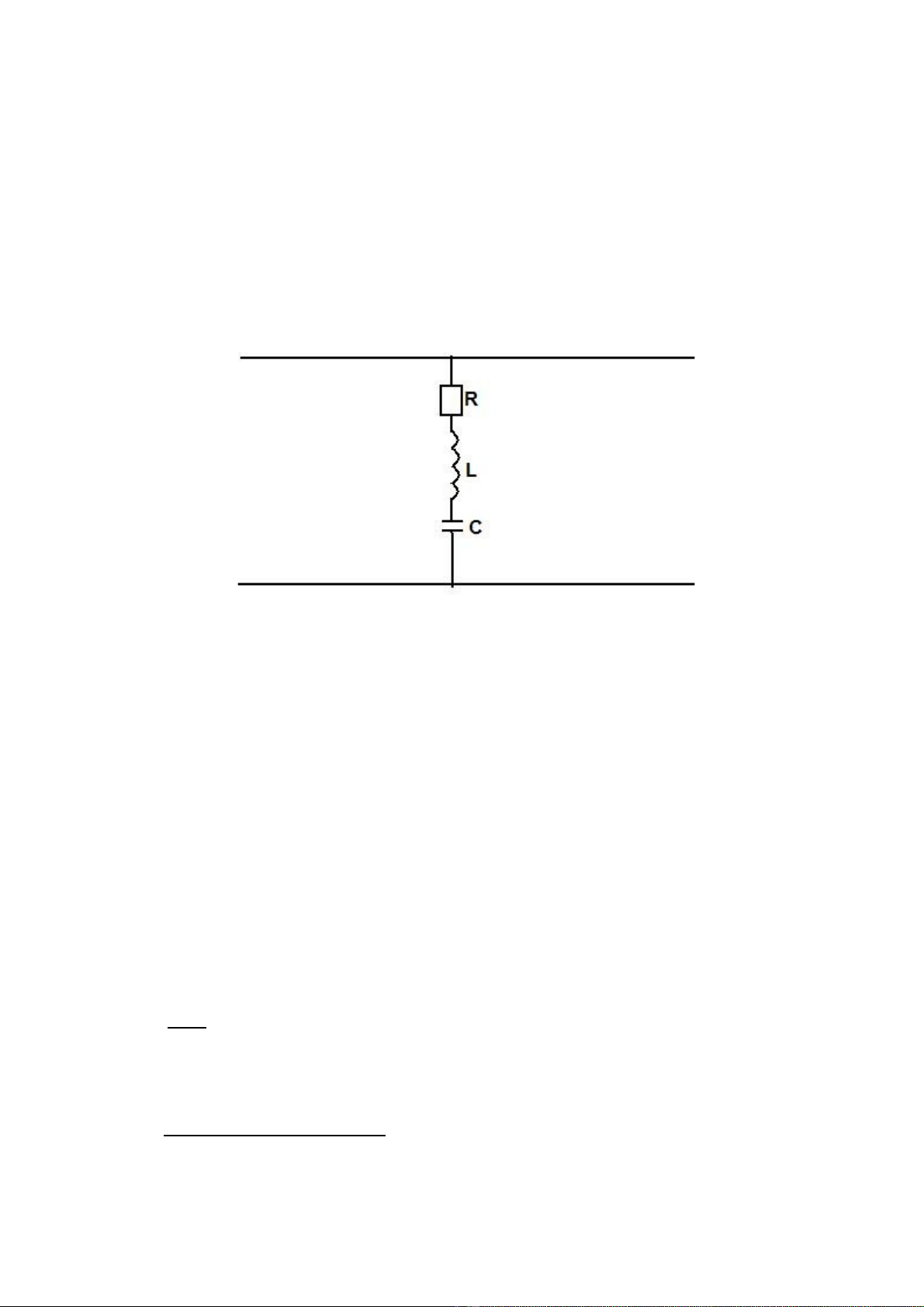
Đ bài : ềHãy xác đ nh 2 d ng ph ng trình đ c tínhị ạ ươ ặ
b t kỳ c a m ch 4 c c trong đó ấ ủ ạ ự
R= 10Ω ;
ω
L=5Ω ;1/
ω
C=5Ω.
L i gi i : ờ ả
Ph ng trình đ c tính tr kháng h m ch:ươ ặ ở ở ạ
Bi t Iế1,I2
→
U1, U2
U1 = Z11I1 + Z12I2
U2 = Z21I1 + Z21I2
→
Z11 =
1
1
I
U
khi I2 =0
=
1
).(1
I
ZcZlRI
++
=R +Zl +Zc = 10+5j+5/j(Ω)