Đơn Cực Từ (Phần 2)

Đơn Cực Từ (Phần 2)

Hệ phương trình Mắc-xoen

Định luật Gau-xơ cho từ học

Định luật Gau-xơ cho từ học một trong những phương trình

cơ bản của điện từ học – là một cách hình thức để ta diễn

đạt kết luận rút ra từ những hiện tượng từ mà ta quan sát

được, cụ thể là không tồn tại các cực từ cô lập. Phương

trình này khẳng định là từ thông toàn phần qua một mặt

Gau-xơ kín phải bằng 0:

Định luật Gau-xơ cho từ học: (p.t 1)

Ta đối chiếu phương trình này với định luật Gau-xơ cho

điện học đó là: (p.t. 2)

Trong cả hai định luật này, tích phân được lấy theo một mặt

Gau-xơ hoàn toàn kín. Việc số không chỉ xuất hiện ở vế

phải của p.t.1 mà không có ở vế phải của p.t. 2 có nghĩa là

trong từ học không có “từ tích tự do” tương ứng với điện

tích tự do trong điện học

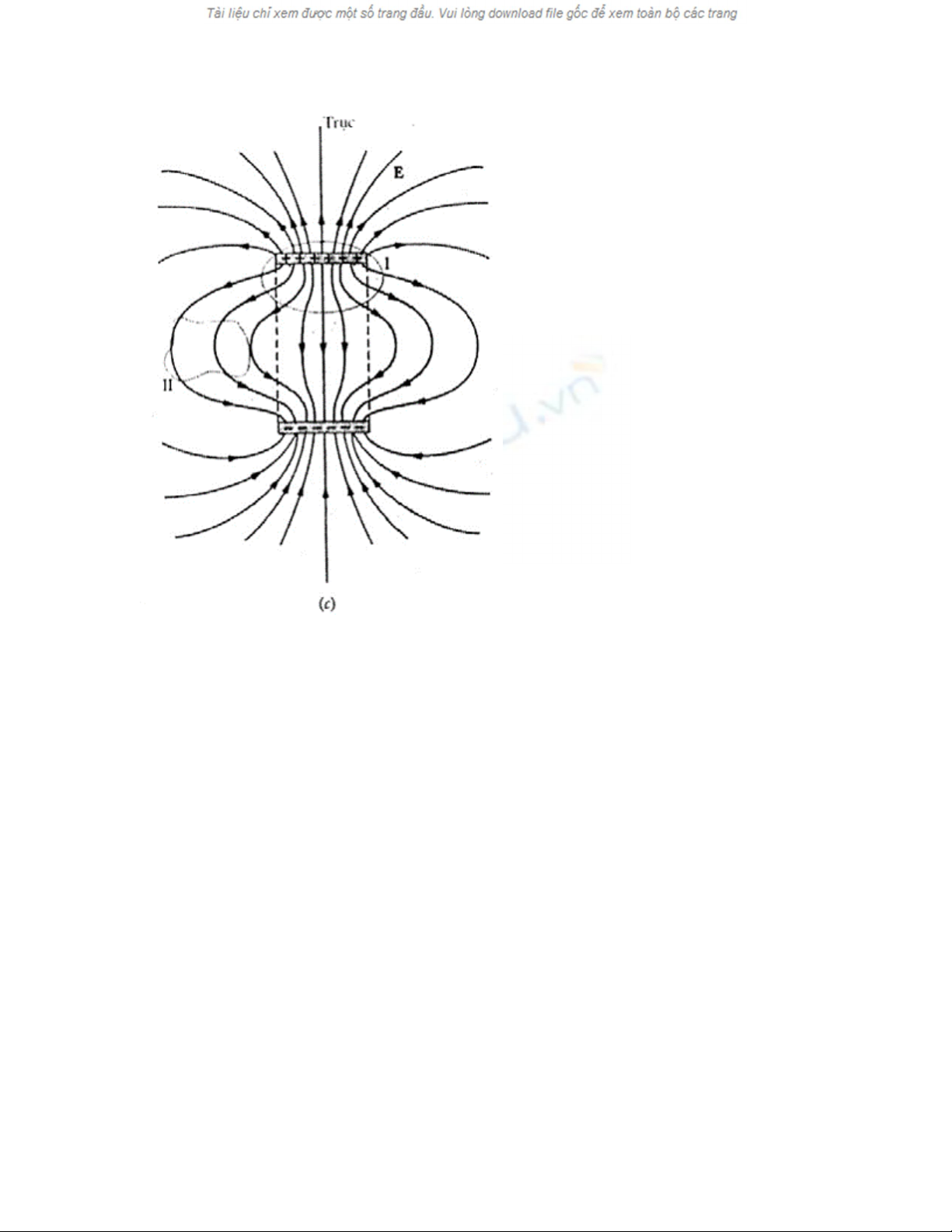
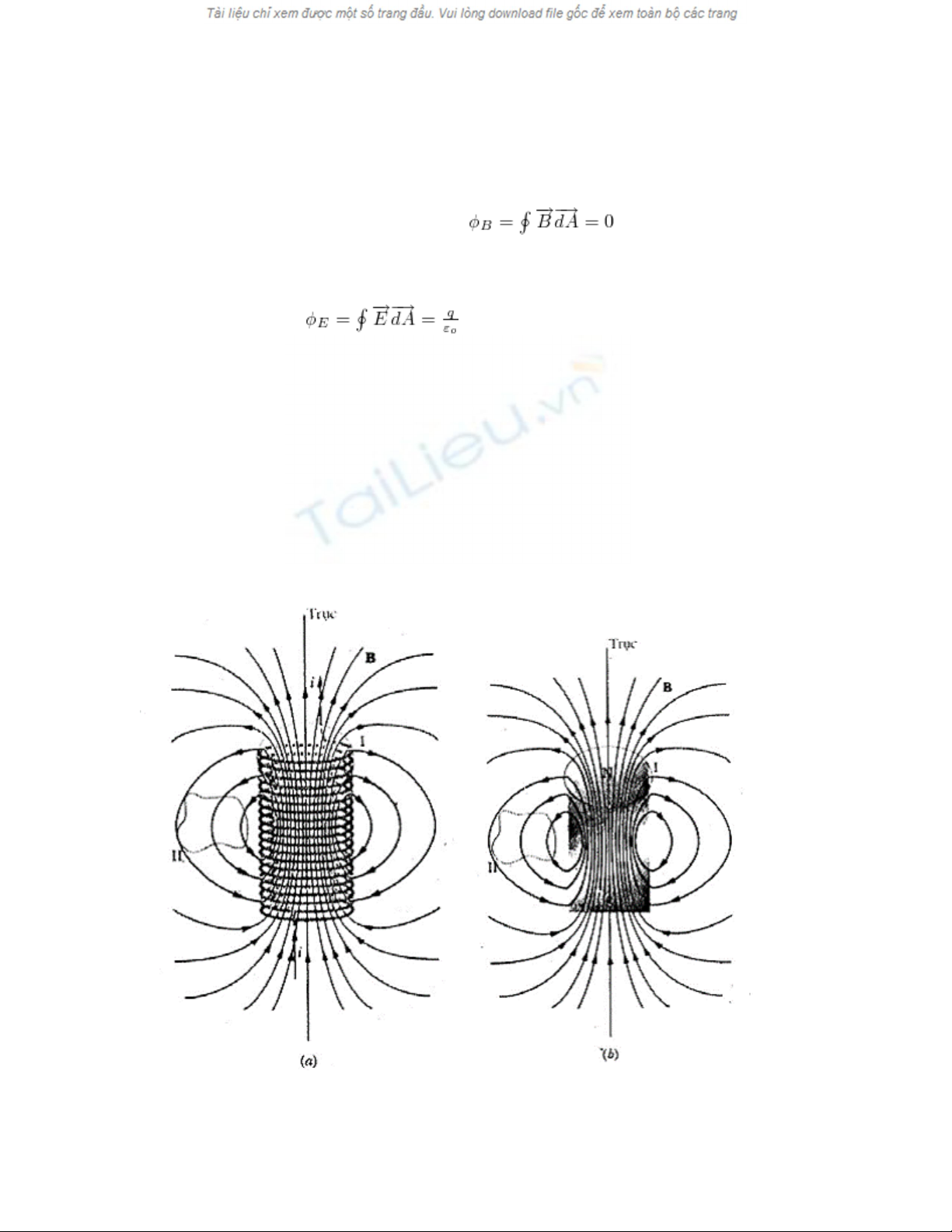
Các đường sức từ của (a) một ống dây thẳng và (b) một

nam châm ngắn. Trong cả hai trường hợp đầu trên đều là

cực bắc. (c) Đường sức điện trường của hai đĩa nhiễm điện.

Ở khoảng cách lớn cả ba trường hợp này giống như trường

cảu một lưỡng cực các đường ký hiệu I và II chỉ các mặt

Gau-xơ kín

Hình a cho thấy mặt Gau-xơ được đánh dấu I, bao một đầu

của ống dây ngắn. Như đã thấy, ống dây thẳng như vậy tạo

ra một từ trường giống trường của một lưỡng cực từ ở

khoảng cách xa. Đối với những điểm xa như thế, đầu của

ống dây thẳng bị bao bởi mặt I thể hiện giống cực từ bắc.

Lưu ý đường sức từ đi vào mặt Gau-xơ ở trong ống dây

thẳng và đi ra khỏi mặt ở ngoài ống dây thẳng. Không có

đường nào được sinh ra hoặc kết thúc ở trong mặt này, nói

cách khác không có nguồn sinh hoặc hủy , hay nói cách

khác nữa không có các cực từ tự do. Như vậy đối với mặt I

ở hình a, thông lượng toàn phần bằng 0, như định luật

Gau-xơ cho từ học (p.t. 1) đòi hỏi.

Ta cũng có bằng không cho mặt II trên hình b, và cho

mọi mặt kín có thể vẽ trên hình này. Sự việc cũng không

thay đổi nếu ta thay ống dây thẳng ngắn bằng một thỏi nam

châm ngắn, như trên hình b. Ở đây cũng bằng 0 cho mọi

mặt kín mà ta có thể vẽ.

Hình c cho thấy một sự tương tự tĩnh điện với hai lưỡng

cực từ này. Nó gồm hai đĩa tròn tích điện trái dấu đặt đối

diện với nhau. Ở những điểm ở xa điện trườg của hệ đĩa

này cũng là điện trường của một lưỡng cực. Tuy nhiên,

trong trường hợp này có thông lượng toàn phần (hướng ra

ngoài) của đường sức qua mặt Gau-xơ đánh dấu I; có

nguồn sinh ở bên trong mặt, cụ thể là mặt I bao quanh điện

tích dương (các điện tích âm ở đĩa kia hủy các đường sức

điện trường). Dĩ nhiên đối với mặt Gau-xơ đánh dấu II

ở hình c, ta có vì mặt này không bao điện tích gì cả.

Các phương trình cơ bản của điện từ học

Định luật Gau-xơ về điện học (p.t. 3)

Định luật Gau-xơ về từ học (p.t. 4)

Định luật cảm ứng của Fa-ra-đây (p.t. 5)

Định luật Am-pe (p.t. 6)

Sự bất đối xứng thứ nhất

Sự bất đối xứng này gắn liền một sự thực là trong tự nhiên

tồn tại các tâm tích điện cô lập như electron, proton…

nhưng hình như không có các tâm mang từ tích (đơn cực

từ). Như vậy ta phải đoán nhận như thế nào về việc có đại

lượng q ở vế phải của p.t. 3 nhưng lại không có đại lượng

từ tương tự ở vế phải của p.t. 4. Tương tự như vậy vế phải

của p.t.6 có số hạng nhưng vế phải của p.t. 5 lại

không có số hạng tương tự (tức là dòng của các đơn cực

từ).

“Sự thiếu đối xứng” này, kết hợp với sự tiên đoán chi tiết

của vài lí thuyết sơ bộ về bản chất của các hạt sơ cấp và các

lực, đã thúc đẩy các nhà vật lí tìm kiếm một cách rất

nghiêm túc và bằng nhiều con đường khác nhau các đơn

cực từ, song không ai tìm thấy cả. Tuy nhiên cũng có một

vài đầu mối, như thể thiên nhiên đang gợi ý và hướng dẫn

các nhà vật lí trên bước đường khám phá của họ.

Sự bất đối xứng thứ hai

Sự bất đối xứng này nổi cộm lên như một ngón tay đau

vậy: ở vế phải của định luật Fa-ra-đây về cảm ứng (p.t. 5)

ta thấy có số hạng , và ta đoán nhận định luật này

một cách linh hoạt như sau: Nếu ta thay đổi một từ trường

ta sẽ tạo ra một điện trường Từ nguyên lí đối

xứng, ta có quyền nghĩ rằng phải có một quan hệ đối xứng

với quan hệ trên, cụ thể là: Nếu ta thay đổi một điện trường

ta sẽ tạo ra một từ trường này chỉ dựa trên

đơn thuần vào lập luận đối xứng và đã tỏ ra là đúng khi ta

kiểm tra bằng thực nghiệm trong phòng thí nghiệm – Nó

cung cấp cho chúng ta số hạng còn thiếu trong p.t 6.

Thật khó tin rằng ở đây thiên nhiên lại cố tình xoá bỏ đi

tính đối xứng đẹp đẽ vốn có của mình. Một số nhà vật lí đã

nghĩ như vậy. Do đó ngay sau khi lí thuyết Mắc-xoen vừa

mới ra đời, người ta cố tìm những bằng chứng chứng tỏ

rằng trong tự nhiên có từ tích. Người ta coi lớp từ tích kép

(tương tự lớp điện tích kép) là một trong những bằng chứng

đó. Một số nhà vật lí có niềm tin vào sự tồn tại của các từ

tích rất mãnh liệt. Họ coi định luật tương tác giữa các từ

tích cũng giống như định luật tương tác giữa các điện tích,

nghĩa là tương tác giữa các từ tích cũng tuân theo định luật

Cu-lông

Trong một thời gian dài không có một quan sát nào, không

có một sự kiện thực nghiệm nào chứng tỏ về sự tồn tại của

các từ tích. Vì vậy giả thiết về từ tích, về định luật tương

tác giữa các từ tích hầu như không được nhắc đến.

Tuy nhiên, điều đó không có nghĩa là giả thiết về từ tích đã

bị loại bỏ, mà ngược lại, nó còn được khôi phục và phát

triển. Việc khôi phục này bắt đầu từ ý kiến của Đi-rắc, một

trong những nhà vật lí lỗi lạc nhất của thời đại chúng ta

Paul Adrien maurice Dirac (1902-1984)

Nhà vật lí lí thuyết người Anh

Năm 1931, Đi-rắc đưa thêm vào trong hệ phương trình

Mắc-xoen đại lượng từ tích và dòng từ (nói đúng hơn là

mật độ từ tích và mật độ dòng từ) tương tự như điện tích và

dòng điện.Việc đưa ra các đại lượng đó xuất phát từ lập

luận của ông là, không có một định luật vật lí nào cấm khả

năng tồn tại các từ tích dương, các từ tích âm một cách tách

biệt nhau. Hay nói đúng hơn là cho đến lúc đó chưa tìm

thấy một định luật nào như thế. Đi-rắc gọi các từ tích

dương, các từ tích âm tồn tại một cách tách biệt là các đơn

cực từ. Ý tưởng đó sẽ được trình bày trong bài viết tiếp

theo