
Trường THPT BC Nguyễn Trường Tộ GIÁO ÁN ĐIỆN TỬ
Gv:Nguyễn Đức Diệu Trang
Tiết 25 ÔN TẬP CUỐI HỌC KỲ I
----oOo----
I. MỤC TIÊU BÀI DẠY
1. Về hình thức:
Học sinh nhớ lại những kiến thức cơ bản nhất đã được học trong chương I,II :
Tổng,hiệu của hai vectơ,tích của vectơ với một số,trục toạ độ,hệ trục toạ độ,giá trị của
một góc bất kỳ,tích vô hướng của hai vectơ,hệ thức lượng trong tam giác.
2. Về kỹ năng :
Dùng kiến thức về tích vô hướng để xác định trực tâm,trọng tâm,tâm đường tròn
ngoại tiếp tam giác.
Sử dụng định lý sin tính bán kính đường tròn ngoại tiếp.
Công thức tính diện tích tam giác để giải quyết một số bài toán tính toán hình học.
3. Về tư duy và thái độ :
Biết chuyển đổi giữa bài toán hình học tổng hợp -toạ độ-vectơ.
Biết đầu hiểu được việc đại số hoá hình học.
Tích cực hoạt động,có tinh thần làm việc tập thể.
II. CHUẨN BỊ
Bảng hệ thống kiến thức
Các hình vẽ.
Máy chiếu.
Đề bài phát cho học sinh.
III. PHƯƠNG PHÁP DẠY HỌC
1.Gợi mở vấn đáp.
2.Chia nhóm nhỏ để học tập.
IV.TIẾN TRÌNH BÀI DẠY VÀ CÁC HOẠT ĐỘNG
Hoạt động 1 : Giáo viên trình chiếu bảng hệ thống kiến thức của chương I,chương
II và nhắc lại cho học sinh,không đi sâu.
1. Vectơ
. Vectơ Oa
. Vectơ O
. Vectơ
CDAB
CDAB
CDAB híng cïng ,
2. Tổng và hiệu các vectơ
. Quy tắc ba điểm : Với M,N,P bất kỳ ta có: MPNPMN .
. Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì ACADAB .
. Quy tắc về hiệu hai vectơ : Cho vectơ MN ,với điểm O bất kỳ ta có:
OMONMN
3. Tích của vectơ với một số
. Nếu akb thì bcùng hướng với a khi k 0
bngược hướng với a khi k 0
và độ dài đại số akb
.
. Điểm M là trung điểm của AB
với mọi điểm O bất kỳ ta có
OBOAOM 2
1
. Điểm G là trọng tam giác ABC
với mọi điểm O bất kỳ ta có:
OCOBOAOG 3
1.
Trường THPT BC Nguyễn Trường Tộ GIÁO ÁN ĐIỆN TỬ
Gv:Nguyễn Đức Diệu Trang
4. Toạ độ của vectơ và của điểm
.Nếu A(x,y),B(x',y') thì
yyxxAB ','
.Nếu u(x,y) và v(x',y') thì
',' yyxxvu
kykxuk ,
5. Giá trị lượng giác của một góc.
6. Tích vô hướng của hai vectơ: baba
.. .cos ),( ba
Biểu thức toạ độ của tích vô hướng
Nếu a(x,y) và b(x',y') thì '.'.. yyxxba
7.Định lý cosin trong tam giác: bacba .2
222 cosA
8.Định lý sin trong tam giác:
R
c
c
b
b
a
a2
sin
sin
sin
9.Công thức trung tuyến của tam giác:
4
2
222
2acb
ma
10.Công thức tính diện tích tam giác:
))()((
4
sin.
2
1
.
2
1cpbpapppr
R
abc
cabhaS a
Hoạt động 2: Giáo viên phát đề bài tập :
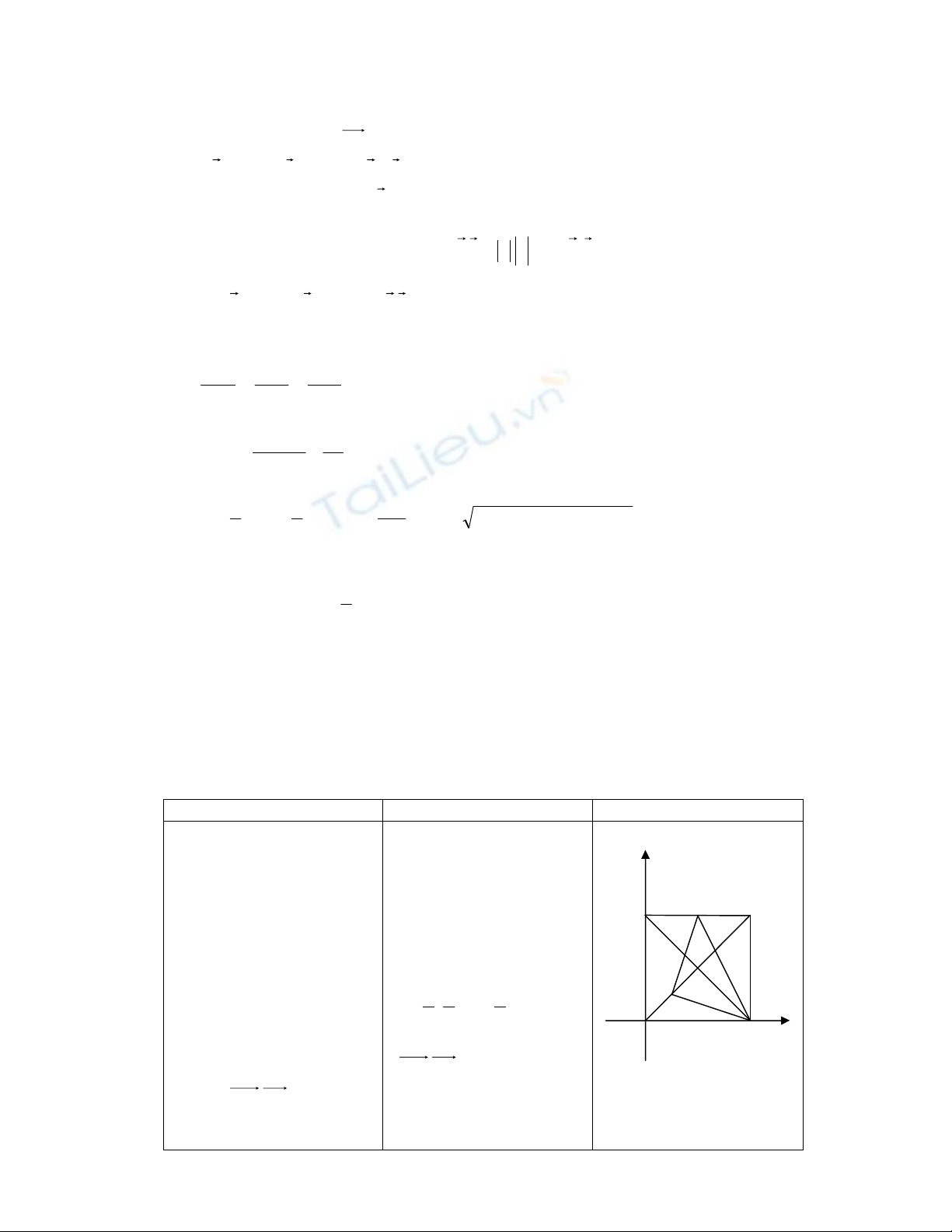
Đề bài tập : Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD. M là điểm
trên AC sao cho ACAM
4
1
a. Tìm toạ độ trực tâm của tam giác BMN. Nhận xét gì về vị trí của trực tâm? Tính
góc
BMN ?.
b. Tìm toạ độ tâm I đường tròn ngoại tiếp tam giác BMN.
c. Tính chu vi tam giác BMN.Nhận xét gì về tam giác BMN.
d. Tính diện tích tam giác BMN.
e. Tính bán kính đường tròn nội tiếp tam giác BMN.
Hoạt động 3 : Tiến hành tìm lời giải câu hỏi 1.
Tìm toạ độ trực tâm của tam giác BMN.
Hoạt động của giáo viên Hoạt động của học sinh Màn hình
- Giáo viên định hướng cho
học sinh giải bài tập theo
phương pháp toạ độ.
- Giáo viên vẽ hình,lập hệ
trục toạ độ vuông góc với
gốc trùng với điểm A sao
cho :
A(0,0),B(a,0),C(a,a),D(0,a).
- Yêu cầu học sinh tìm toạ
độ M,N.
- Gọi H(x,y) là trực tâm tam
giác BMN.
- Yêu cầu học sinh cho biết
kết quả BNMH.?
- Yêu cầu học sinh làm
nhóm để tìm toạ độ H.
- Học sinh vẽ hình.
-M
4
,
4
aa ;N
a
a,
2.
-0. BNMH .
y
N
D C
M
a x
A
O B
Trường THPT BC Nguyễn Trường Tộ GIÁO ÁN ĐIỆN TỬ
Gv:Nguyễn Đức Diệu Trang
- Giáo viên giúp đỡ khi cần
thiết và chính xác hoá kết
quả bằng trình chiếu trên
màn hình.
- Hỏi học sinh có nhận xét
gì về vị trí điểm H ? và góc
BMN ?
- Từ đó học sinh có thể
nhanh chóng chuyển qua
câu b.
- Học sinh tìm toạ độ trực
tâm H.
0
90
BMN
M
H
- Chọn hệ trục toạ độ
A(0,0),B(a,0),C(a,a),D(0,a)
N( a
a,
2
),M(
4
,
4
aa ).
Gọi H(x,y)
4
,
4
a
y
a
xMH
a
a
BN ,
2
Ta có 0. BNMH
0
4
0
42
a
ya
a
x
a
4
4
a
y
a
x
Suy ra H(
4
,
4
aa )
Vậy
M
H
Hoạt động 4 : Tìm toạ độ tâm I đường tròn ngoại tiếp.
Hoạt động của giáo viên Hoạt động của học sinh Màn hình
- Ở câu a ta có
0
90
BMN .Giáo viên đặt
câu hỏi tâm đường tròn
ngoại tiếp tam giác BMN
nằm ở vị trí nào? Có toạ độ?
- Sau đó chiếu kết quả lên
màn hình cho học sinh.
- I là trung điểm BN.
2
,
4
3
2
0
,
22
2
,
2
aa
I
a
a
a
I
yyxx
INBNB
- Ta có 0
90
BMN .
Gọi I là trung điểm BN.
Lúc đó IM=IN=IB.
Vậy I là tâm đường tròn
ngoại tiếp tam giác BMN.
22
02
4
3
22
2
aa
yy
y
a
a
a
xx
x
I
NB
I
NB
I
Vậy
2
,
4
3aa
I.
Trường THPT BC Nguyễn Trường Tộ GIÁO ÁN ĐIỆN TỬ
Gv:Nguyễn Đức Diệu Trang
Hoạt động 5 : Tiến hành tìm chu vi tam giác BMN.Nhận xét gì về tam giác BMN.
Hoạt động của giáo viên Hoạt động của học sinh Màn hình
- Giáo viên hướng dẫn học
sinh để tìm chu vi thì ta cần
tìm ?
- Giáo viên tổ chức cho học
sinh làm nhóm.
- Chọn một học sinh lên
trình bày và nhận xét gì về
tam giác BMN.
- Chính xác hoá kết quả
bằng cách chiếu lên màn
hình.
- Ba cạnh MN,NB,MB.
- Học sinh làm nhóm.
- Học sinh trình bày kết
quả của nhóm.
- Ta có
4
,
4
3aa
MB
a
a
NB ,
2
4
3
,
4
aa
MN
Do đó
4
10
16
10
1616
9
2
22
aa
aa
MBMB
2
5
4
5
4
2
2
2
aa
a
a
NBNB
4
10
16
10
16
9
16
2
22
aa
aa
MNMN
Vậy C=MB+NB+MN=
=
4
10
2
5
4
10 aaa
=
510
2
a
Ta có
MB=MN và 0
90
BMN
Vậy tam giác BMN vuông
cân tại M.
Hoạt động 6 :
Hoạt động của giáo viên Hoạt động của học sinh Màn hình
- Từ kết quả câu c: Tam giác
vuông cân tại M
- Giáo viên hỏi học sinh
công thức tính diện tích tam
giác BMN.
- Diện tích tam giác BMN
2
2
1
.
2
1MNMBMNS
Ta có:
Tam giác BMN vuông cân
tại M,do đó diện tích tam
giác BMN là :

Trường THPT BC Nguyễn Trường Tộ GIÁO ÁN ĐIỆN TỬ
Gv:Nguyễn Đức Diệu Trang
- Yêu cầu học sinh tính
nhanh kết quả.
- Giáo viên trình chiếu lên
màn hình kết quả chính xác.
16
5
16
10
.
2
1
2
1
.
2
1
22
2
aa
MNMBMNS
Vậy
16
52
a
S
Hoạt động 7 :
Hoạt động của giáo viên Hoạt động của học sinh Màn hình
- Từ kết quả câu c,d giáo
viên đặt câu hỏi cho học
sinh liên tưởng đến công
thức nào để tính bán kính
đường tròn nội tiếp tam
giác.
- Yêu cầu học sinh tính
nhanh.
- Giáo viên trình chiếu kết
quả chính xác lên màn hình.
- Học sinh đưa ra công
thức : rpS .
Theo câu c,d ta có
C=
510
2
a
Suy ra p=
510
4
a
S=
16
52
a
Mặt khác rpS .
Suy ra
)510(4
5
a
p
S
r


























