BomonKTDT-§HGTVT
113
Ch−¬ng 11
M¹ch d∙y ®ång bé
M¹ch d·y ®ång bé lµ mét m¹ch sè bao gåm c¸c m¹ch tæ hîp vµ c¸c phÇn
tö nhí FF, m¹ch ho¹t ®éng theo sù ®ång bé cña xung nhÞp Ck.
I. Ph©n tÝch
Bµi to¸n ph©n tÝch lµ bµi to¸n x¸c ®Þnh chøc n¨ng cho tr−íc;
- S¬ ®å m¹ch:
Tõ s¬ ®å m¹ch cho tr−íc cÇn x¸c ®Þnh chøc n¨ng tõng phÇn tö c¬ b¶n cña s¬ ®å, vµ
mèi liªn hÖ gi÷a c¸c s¬ ®å ®ã
- X¸c ®Þnh ®Çu vµo, ®Çu ra, sè tr¹ng th¸i trong cña m¹ch:
Coi m¹ch nh− mét hép ®en, cÇn ph¶i x¸c ®Þnh sè ®Çu vµo, ®Çu ra, ®Æc ®iÓm c¸c ®Çu
vµo ra, x¸c ®Þnh tr¹ng th¸i cña m¹ch
- X¸c ®Þnh ph−¬ng tr×nh hµm ra, hµm kÝch cho c¸c FF
Dùa vµo s¬ ®å cho tr−íc x¸c ®Þnh hÖ ph−¬ng tr×nh hµm ra, hµm kÝch cho c¸c FF
- LËp b¶ng tr¹ng th¸i, b¶ng ra nhÞ ph©n:
B¶ng tr¹ng th¸i, b¶ng ra nhÞ ph©n lµ b¶ng biÓu diÔn quan hÖ gi÷a tr¹ng th¸i chuyÓn
®Õn, tÝn hiÖu ra nhÞ ph©n víi tr¹ng th¸i hiÖn t¹i vµ tÝn hiÖu vµo t−¬ng øng. Dùa vµo
c¸c ph−¬ng tr×nh hµm kÝch, hµm ra x¸c ®Þnh ®−îc ë trªn, vµ dùa vµo ph−¬ng tr×nh
®Æc tÝnh cña FF x¸c ®Þnh ®−îc tr¹ng th¸i chuyÓn tíi vµ tÝn hiÖu ra t−¬ng øng víi tÝn
hiÖu vµo vµ tr¹ng th¸i hiÖn t¹i cña m¹ch.
- §å h×nh tr¹ng th¸i:
Tõ b¶ng tr¹ng th¸i vµ b¶ng ra ®· lËp ë trªn, x©y dùng ®−îc ®å h×nh tr¹ng th¸i vµ tÝn
hiÖu ra cña m¹ch.
- Chøc n¨ng cña m¹ch:
Sau khi lËp ®−îc ®å h×nh tr¹ng th¸i, dùa vµo ®å h×nh ®ã x¸c ®Þnh ®−îc chøc n¨ng
cña m¹ch. Cô thÓ lµ tõ sù ph©n tÝch ®ã mµ rót ra ®−îc chøc n¨ng cña m¹ch.
II. ThiÕt kÕ
1. C¸c b−íc thiÕt kÕ:
C¸c b−íc thiÕt kÕ ng−îc l¹i víi c¸c b−íc ph©n tÝch, tuy nhiªn m¹ch thiÕt kÕ ph¶i
thùc hiÖn chøc n¨ng cho tr−íc víi s¬ ®å cµng ®¬n gi¶n cµng tèt, ®iÒu nµy ®ång
nghÜa víi viÖc tèi thiÓu ho¸ tr¹ng th¸i.
- B−íc 1: X¸c ®Þnh bµi to¸n
§©y lµ b−íc ®Çu tiªn vµ còng lµ b−íc quan träng ®Ó thùc hiÖn tèt viÖc thiÕt kÕ m¹ch,
tr−íc tiªn ph¶i x¸c ®Þnh ®−îc yªu cÇu ®Æt ra cho m¹ch vµ ph¶i x¸c ®Þnh m¹ch ®−îc
thiÕt kÕ tõ nh÷ng yÕu tè nµo?
- B−íc 2: X¸c ®Þnh tÝn hiÖu vµo/ra:
X¸c ®Þnh tÝn hiÖu vµo, ra còng nh− ®Æc ®iÓm cña chóng
- B−íc 3: X©y dùng ®å h×nh tr¹ng th¸i, b¶ng tr¹ng th¸i, b¶ng tÝn hiÖu ra
Nãi chung viÖc x©y ®å h×nh tr¹ng th¸i kh«ng dùa trªn mét quy t¾c nµo, mµ
phÇn lín dùa vµo kinh nghiÖm cña ng−êi thùc hiÖn, nh−ng quy t¾c lµ dùa vµo yªu
cÇu cña bµi to¸n ®Æt ra(tÝn hiÖu vµo ra ), tõ ®ã lËp ®å h×nh tr¹ng th¸i, x¸c ®Þnh ®−îc
®iÒu kiÖn ®Ó cho m¹ch cã thÓ chuyÓn ®æi tõ tr¹ng th¸i nµy sang tr¹ng th¸i tiÕp theo
vµ khi nµo th× m¹ch cho tÝn hiÖu ra.
PTH-DTT
114
Tõ ®å h×nh tr¹ng th¸i lËp trªn, x©y dùng b¶ng tr¹ng th¸i vµ b¶ng tÝn hiÖu
ra
- B−íc 4: Tèi thiÓu ho¸
Nh− ®· biÕt sè tr¹ng th¸i trong cña m¹ch gÇn nh− tØ lÖ víi sè FF ®−îc dïng trong
m¹ch, viÖc tèi thiÓu ho¸ tr¹ng th¸i chñ yÕu dùa vµo kh¸i niÖm t−¬ng ®−¬ng, ta sÏ
xÐt sau.
- B−íc 5: M· ho¸ nhÞ ph©n
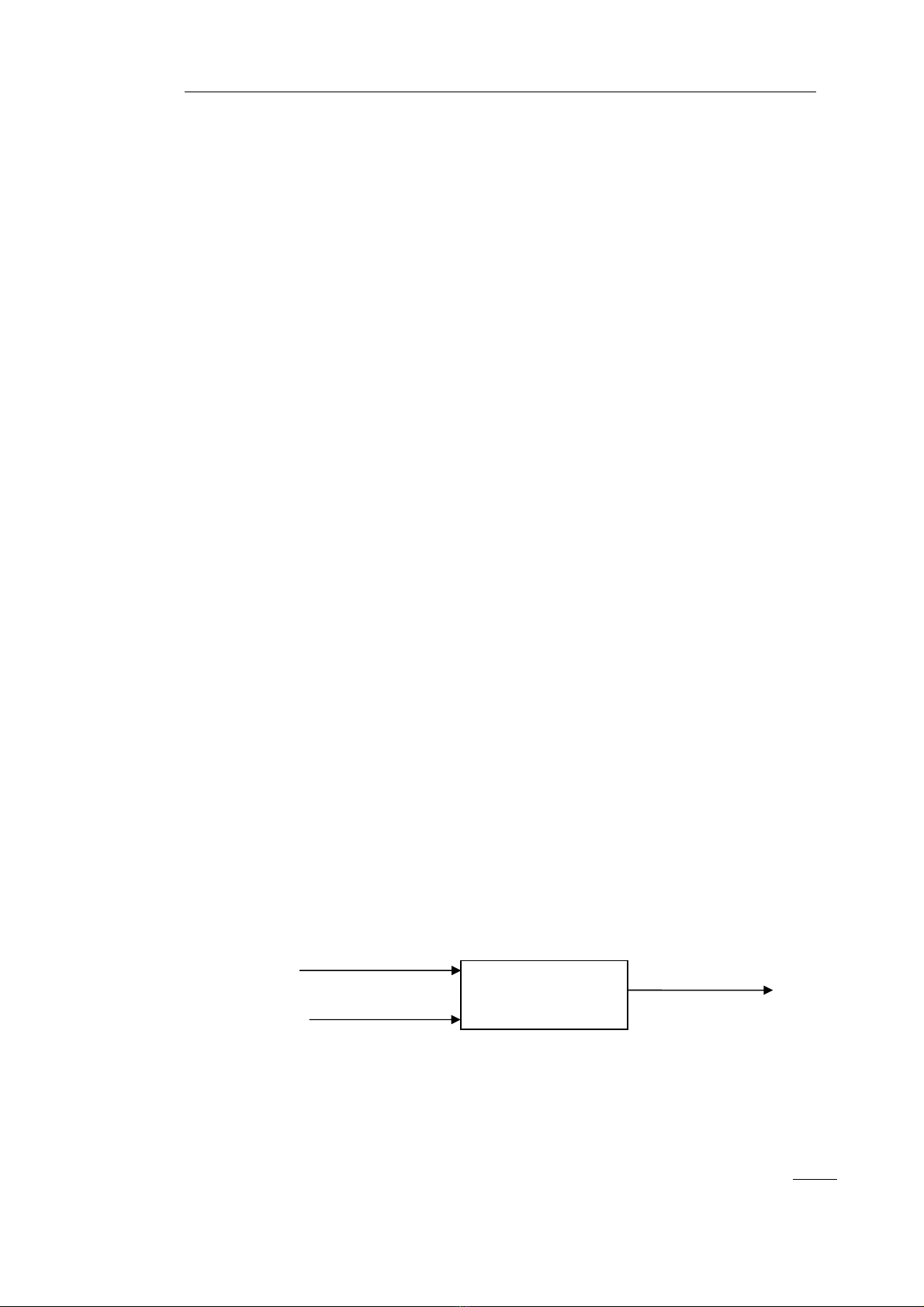
X¸c ®Þnh bµi to¸n
X¸c ®Þnh tÝn hiÖu vµo ra
§å h×nh tr¹ng th¸i, b¶ng tr¹ng th¸i, b¶ng ra
Rót gän tr¹ng th¸i
M· ho¸ nhÞ ph©n
X¸c ®Þnh hÖ ph−¬ng tr×nh cña m¹ch
S¬ ®å m¹ch thùc hiÖn
BomonKTDT-§HGTVT
115
Sau khi tèi thiÓu ho¸ c¸c tr¹ng th¸i, vµ ®−a vµo ®å h×nh tr¹ng th¸i t−¬ng øng, dïng
c¸c biÕn nhÞ ph©n ®Ó m· ho¸ cho c¸c tr¹ng th¸i, sè biÕn nhÞ ph©n dïng ®Ó m· ho¸
c¸c tr¹ng th¸i phô thuéc vµo sè tr¹ng th¸i trong.
NÕu sè l−îng tr¹ng th¸i trong lµ N, sè l−îng biÕn nhÞ ph©n dïng lµ n, th× n
ph¶i tho¶ m·n ®iÒu kiÖn: n≥log2N
Cã nhiÒu c¸ch ®Ó m· ho¸ kh¸c nhau, mçi c¸ch cho mét s¬ ®å kh¸c nhau, yªu
cÇu ph¶i m· ho¸ sao cho s¬ ®å lµ ®¬n gi¶n nhÊt.
- B−íc 6: X¸c ®Þnh hÖ ph−¬ng tr×nh cña m¹ch:
Sau khi ®· m· ho¸ ®−îc c¸c tr¹ng th¸i trong cña m¹ch, cã thÓ x¸c ®Þnh hÖ
ph−¬ng tr×nh cña m¹ch theo 2 c¸ch:
+ LËp b¶ng chuyÓn ®æi tr¹ng th¸i vµ tÝn hiÖu ra nhÞ ph©n, tõ ®ã x¸c ®Þnh ®−îc
ph−¬ng tr×nh ®Çu vµo kÝch cho c¸c FF vµ ph−¬ng tr×nh cña tÝn hiÖu ra, sau ®ã chóng
ta tiÕn hµnh tèi thiÓu ho¸ c¸c ph−¬ng tr×nh ®ã.
+ Dùa trùc tiÕp vµo ®å h×nh tr¹ng th¸i, viÕt hÖ ph−¬ng tr×nh Ton , Toff cña c¸c FF vµ
ph−¬ng tr×nh tÝn hiÖu ra cña m¹ch sau ®ã tiÕn hµnh tèi thiÓu ho¸ hÖ ph−¬ng tr×nh ®ã.
- B−íc 7: S¬ ®å m¹ch thùc hiÖn
Tõ c¸c ph−¬ng tr×nh ®· x¸c ®Þnh ®−îc ta x©y dùng s¬ ®å m¹ch
III. Tèi thiÓu ho¸:
NhiÖm vô ®Æt ra cho ng−êi thiÕt kÕ lµ ph¶i ®−a ra m¹ch ho¹t ®éng ®óng chøc
n¨ng cho tr−íc, s¬ ®å cµng ®¬n gi¶n cµng tèt, muèn vËy cÇn gi¶m nhá sè trang th¸i
trong.
ViÖc tèi thiÓu ho¸ chñ yÕu dùa vµo kh¸i niÖm"tr¹ng th¸i t−¬ng ®−¬ng", bµi
to¸n tèi thiÓu ho¸ tr¹ng th¸i chÝnh lµ bµi to¸n ®i t×m líp tr¹ng th¸i t−¬ng ®−¬ng lín
nhÊt, vµ ®−îc thay b»ng mét tr¹ng th¸i ®¹i diÖn, sè tr¹ng th¸i t−¬ng ®−¬ng chÝnh lµ
sè tr¹ng th¸i tèi thiÓu. Cã 3 ph−¬ng ph¸p tèi thiÓu hay dïng:
1, Ph−¬ng ph¸p Caldwell:
Ph−¬ng ph¸p nµy ®−îc minh häa qua vÝ dô sau:
ThiÕt kÕ mét m¹ch d·y ®ång bé thùc hiÖn nhiÖm vô kiÓm tra d·y tÝn hiÖu
vµo ë d¹ng nhÞ ph©n cã ®é dµi b»ng 3 ®−îc ®−a vµo liªn tiÕp ®Çu vµo X, nÕu d·y tÝn
hiÖu vµo cã d¹ng 010 huÆc 110 huÆc 111 th× tÝn hiÖu ra Z=1®Ó b¸o hiÖu lµ m¹ch ®·
nhËn ®−îc mét trong c¸c d·y tÝn hiÖu vµo ®ã.
- B−íc 1: X¸c ®Þnh bµi to¸n
M¹ch thiÕt kÕ cã nhiÖm vô ph¸t hiÖn d·y tÝn hiÖu vµo, nÕu d·y tÝn hiÖu vµo
cã d¹ng 010, huÆc 011, huÆc 110 huÆc 111 th× Z=1 ®Ó b¸o hiÖu m¹ch ®· nhËn ®−îc
mét trong c¸c d·y tÝn hiÖu ®ã.
- B−íc 2: X¸c ®Þnh tÝn hiÖu vµo ra
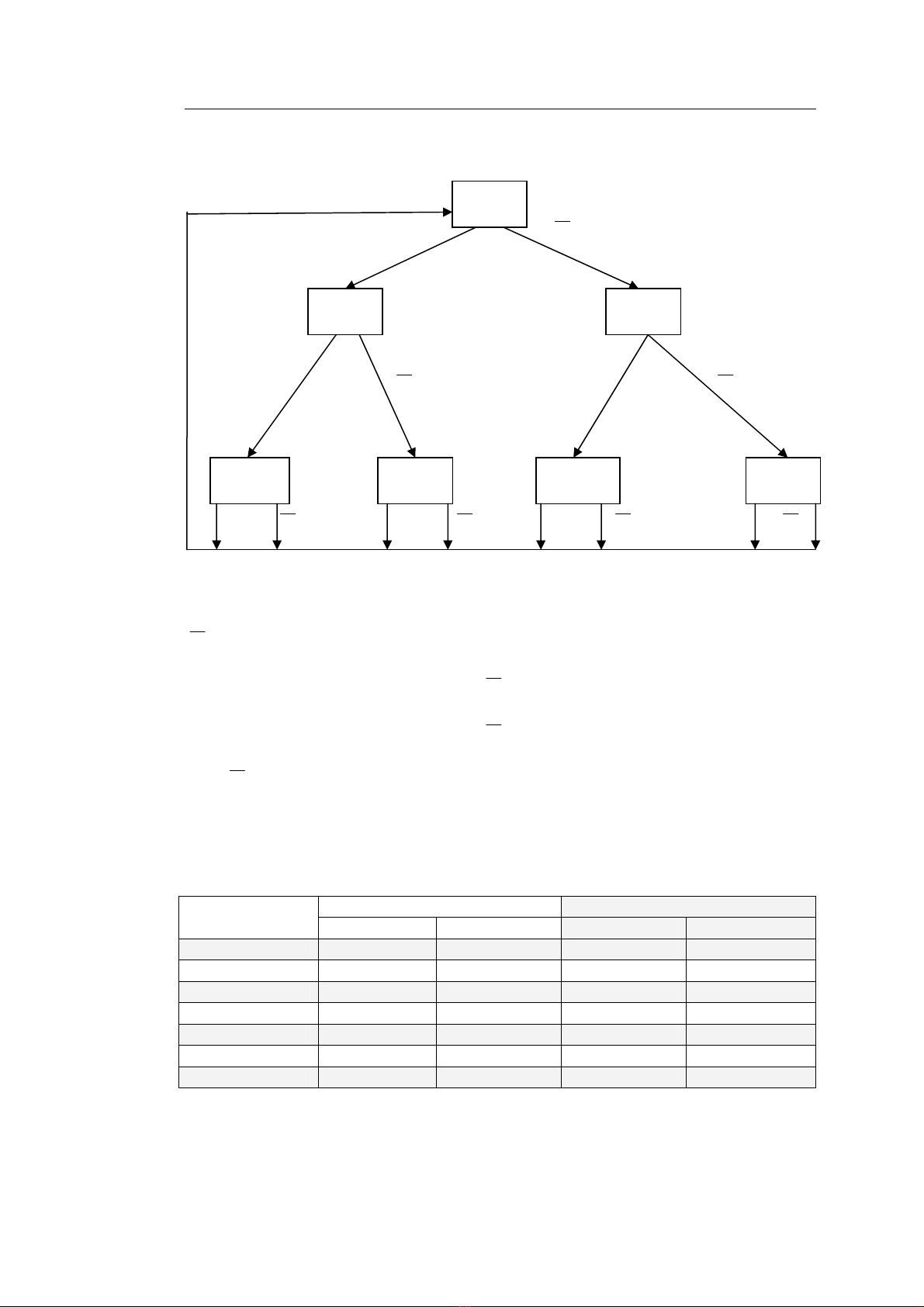
M¹ch ph¶i thiÕt kÕ lµ m¹ch ®ång bé, nªn ngoµi ®Çu vµo X cßn cã ®Çu vµo
xung nhÞp Ck mét ®Çu tÝn hiÖu ra lµ Z, theo d¹ng s¬ ®å khèi nh− sau:
Error!
- B−íc 3: ®å h×nh tr¹ng th¸i, b¶ng tr¹ng th¸i, b¶ng ra: Dùa vµo c¸c yªu cÇu
cña tÝn hiÖu vµo, ra lËp ®−îc ®å h×nh chuyÓn tr¹ng th¸i nh− sau:
S¬ ®å chuyÓn ®æi tr¹ng th¸i:
M¹ch logic
Z
X
Ck
PTH-DTT
116
Tr¹ng th¸i ban ®Çu lµ S0 : khi tÝn hiÖu vµo lµ XCK m¹ch chuyÓn ®Õn S1,
X
CK m¹ch chuyÓn ®Õn S2.
T−¬ng tù víi tr¹ng th¸i S1, m¹ch sÏ chuyÓn ®Õn S3 khi tÝn hiÖu vµo lµ XCK,
m¹ch chuyÓn ®Õn S2 khi tÝn hiÖu vµo lµ
X
CK
T−¬ng tù víi tr¹ng th¸i S2, m¹ch sÏ chuyÓn ®Õn S5 khi tÝn hiÖu vµo lµ XCK,
m¹ch chuyÓn ®Õn S2 khi tÝn hiÖu vµo lµ
X
CK.
NÕu m¹ch ë mét trong 4 tr¹ng th¸i S3, S4, S5, S6, khi cã tÝn hiÖu vµo lµ XCK
huÆc
X
CK m¹ch sÏ chuyÓn ®Õn tr¹ng th¸i ban ®Çu S0, vËy khi d·y tÝn hiÖu vµo lµ
110 huÆc 111 ®−êng chuyÓn ®æi tr¹ng th¸i: S0->S1->S3->S0 hay khi d·y tÝn hiÖu
vµo lµ 010 huÆc 011 ®−êng S0->S2->S5->S0 th× m¹ch sÏ cho tÝn hiÖu ra Z=1 t¹i thêi
®iÓm cña xung nhÞp thø 3. Víi ®−êng chuyÓn ®æi kh¸c Z=0, tõ ®å h×nh tr¹ng lËp
®−îc b¶ng tr¹ng th¸i nh− b¶ng sau:
S' Z
S X=0 X=1 X=0 X=1
S0 S2 S1 0 0
S1 S4 S2 0 0
S2 S6 S5 0 0
S3 S0 S0 1 1
S4 S0 S0 0 0
S5 S0 S0 1 1
S6 S0 S0 0 0
- B−íc 4: Tèi thiÓu ho¸ tr¹ng th¸i, ta sÏ dïng ph−¬ng ph¸p Caldwell:
+ Tr¹ng th¸i t−¬ng ®−¬ng:
000
001 010
100011,Z=1 011,Z=1 110
X
CK
X
CK
XCK
XCK
XCK
X
CK
X
CK
X
CK
X
CK
X
CK XCK
XCK
XCK
X
C
K
0
S
1
2
S
3 S4 S5S6
BomonKTDT-§HGTVT
117
Tr¹ng th¸i Si ®−îc gäi lµ t−¬ng ®−¬ng víi Sj khi vµ chØ khi nÕu lÊy Si vµ Sj lµ
2 tr¹ng th¸i ban ®Çu th× víi mäi tÝn hiÖu vµo cã thÓ cã chóng lu«n lu«n cho tÝn hiÖu
ra gièng nhau.
NÕu cã nhiÒu tr¹ng th¸i t−¬ng ®−¬ng víi nhau tõng ®«i mét th× chóng t−¬ng
®−¬ng víi nhau. §Ó kiÓm tra nhãm c¸c tr¹ng thai t−¬ng ®−¬ng víi nhau kh«ng, cã
thÓ sö dông b¶ng tr¹ng th¸i vµ tÝn hiÖu ra nh− sau:
- Nhãm c¸c tr¹ng th¸i t−¬ng ®−¬ng ph¶i cã nh÷ng hµng trong b¶ng tÝn hiÖu ra gièng
nhau.
- Nhãm c¸c tr¹ng th¸i t−¬ng ®−¬ng ph¶i cã nh÷ng hµng trong b¶ng tr¹ng th¸i ë cïng
mét cét(øng víi cïng tæ hîp tÝn hiÖu vµo ) lµ t−¬ng ®−¬ng. NghÜa lµ øng víi cïng
mét tæ hîp tÝn hiÖu vµo c¸c tr¹ng th¸i sÏ chuyÓn biÕn tíi, cña chóng lµ t−¬ng ®−¬ng.
§iÒu nµy cho thÊy thñ tôc kiÓm tra tÝnh t−¬ng ®−¬ng cña nhãm c¸c tr¹ng th¸i ph¶i
tiÕn hµnh tuÇn tù tõng b−íc cho ®Õn nhãm cã tr¹ng th¸i cuèi cïng, nÕu nhãm cã
tr¹ng th¸i cuèi cïng nµy lµ t−¬ng ®−¬ng th× nhãm tr¹ng th¸i ®−îc kiÓm tra lµ t−¬ng
®−¬ng.
Quy t¾c Caldwell:
Nh÷ng hµng(t−¬ng øng víi tr¹ng th¸i trong) cña b¶ng chuyÓn ®æi tr¹ng th¸i vµ
tÝn hiÖu ra sÏ kÕt hîp víi nhau vµ ®−îc biÓu diÔn mét hµnh chung- ®Æc tr−ng(tr¹ng
th¸i ®Æc tr−ng) cho chóng nÕu nh− chóng tho¶ m·n 2 ®iÒu kiÖn sau:
1- C¸c hµng t−¬ng øng trong ma trËn gièng nhau
2- Trong ma trËn ra, c¸c hµng t−¬ng øng ph¶i tho¶ m·n mét trong 3 ®iÓm:
- C¸c hµng trong ma trËn ph¶i gièng nhau
- C¸c tr¹ng th¸i trong cïng mét cét n»m trong nhãm tr¹ng th¸i ®−îc xÐt
- C¸c tr¹ng th¸i ë trong cïng mét cét lµ c¸c tr¹ng th¸i t−¬ng øng
Sau khi ®· thay thÕ c¸c tr¹ng th¸i t−¬ng ®−¬ng b»ng mét tr¹ng th¸i chung ®Æc
tr−ng cho chóng, lÆp l¹i c¸c c«ng viÖc t×m c¸c tr¹ng th¸i t−¬ng ®−¬ng(c¸c hµng
t−¬ng ®−¬ng) kh¸c, cho tíi khi nµo kh«ng thÓ t×m ®−îc c¸c hµng(c¸c tr¹ng th¸i)
t−¬ng ®−¬ng víi nhau n÷a th× dõng l¹i. Sè tr¹ng th¸i trong b¶ng tr¹ng th¸i lóc ®ã lµ
tèi thiÓu.
¸p dông quy t¾c Caldwell vµo bµi to¸n trªn, trong b¶ng trªn:
S' Z
S X=0 X=1 X=0 X=1
S0 S2 S1 0 0
S1 S4 S2 0 0
S2 S6 S5 0 0
S3 S0 S0 1 1
S4 S0 S0 0 0
S5 S0 S0 1 1
S6 S0 S0 0 0
S4 t−¬ng ®−¬ng S6, S3 t−¬ng ®−¬ng S5, thay thÕ c¸c tr¹ng th¸i t−¬ng ®−¬ng
b»ng tr¹ng th¸i ®Æc tr−ng cho chóng, ch¼ng h¹n thay thÕ S4, S6 b»ng S46, S3 vµ S5
b»ng S35, tõ ®ã lËp ®−îc b¶ng míi nh− sau: