Ch−¬ng 3 lý thuyÕt tuyÕn tÝnh vÒ sãng bÒ mÆt
trong vïng n−íc cã ®é s©u kh«ng ®æi
3.1 C¸c ph−¬ng tr×nh c¬ b¶n vµ ®iÒu kiÖn biªn
3.1.1 C¸c gi¶ thiÕt trong lý thuyÕt sãng tuyÕn tÝnh
Trong ch−¬ng nµy vµ ch−¬ng 4, chØ cã nh÷ng lý thuyÕt c¬ b¶n nhÊt vÒ sãng ®¹i d−¬ng
®−îc tr×nh bµy. Nãi mét c¸ch kh¸c, tÊt c¶ nh÷ng hiÖu øng kh«ng quan träng ®èi víi hiÖn
t−îng sãng träng lùc bÒ mÆt sÏ bÞ bá qua. H¬n n÷a, ®Ó ®¬n gi¶n hãa, c¸c gi¶ thiÕt sau ®©y
®−îc sö dông trong lý thuyÕt sãng tuyÕn tÝnh:
- chÊt láng kh«ng nhít cã mËt ®é kh«ng ®æi (kh«ng nÐn ®−îc vµ ®ång nhÊt) d−íi
¶nh h−ëng cña träng lùc;
- kh«ng cã lùc t¸c ®éng lªn bÒ mÆt tù do phÝa trªn cña chÊt láng;
- cã thÓ bá qua søc c¨ng mÆt ngoµI;
- ®¸y cña chÊt láng lµ ®¸y r¾n, kh«ng thÊm n−íc vµ n»m ngang;
- sãng tuÇn hoµn, ®Ønh dµi vµ lan truyÒn mµ kh«ng thay ®æi h×nh d¹ng.
C¸c th«ng sè ®éc lËp ®ñ ®Ó m« t¶ chuyÓn ®éng sãng t−¬ng øng víi nh÷ng gi¶ thiÕt
trªn lµ:
- khèi l−îng riªng (
ρ
)
- gia tèc träng tr−êng (g)
- ®é s©u trung b×nh (h)
- ®é cao sãng (H)
- b−íc sãng (L)
§é s©u t−¬ng ®èi h/L lµ mét biÕn quan träng ®Ó ®¸nh gi¸ ¶nh h−ëng cña ®¸y lªn
chuyÓn ®éng sãng, nh− ®· tr×nh bµy trong ch−¬ng 1. Tû sè H/L, ®−îc gäi lµ ®é dèc sãng, lµ
th−íc ®o c−êng ®é chuyÓn ®éng sãng. Tû sè nµy kh«ng thÓ v−ît qu¸ mét gi¸ trÞ cho tr−íc
cã bËc 10-1, bëi v× hiÖn t−îng sãng vì.
Trong ch−ong nµy, c¸c ph−¬ng tr×nh c¬ b¶n m« t¶ chuyÓn ®éng sãng víi nh÷ng gi¶
thiÕt trªn sÏ ®−îc rót ra.
Bëi v× sãng ®−îc nghiªn cøu lµ sãng tuÇn hoµn, cã ®Ønh dµi (sãng hai chiÒu hay sãng
®¬n) lan truyÒn mµ kh«ng thay ®æi h×nh d¹ng, nÕu h−íng trôc x theo h−íng lan truyÒn cña
21
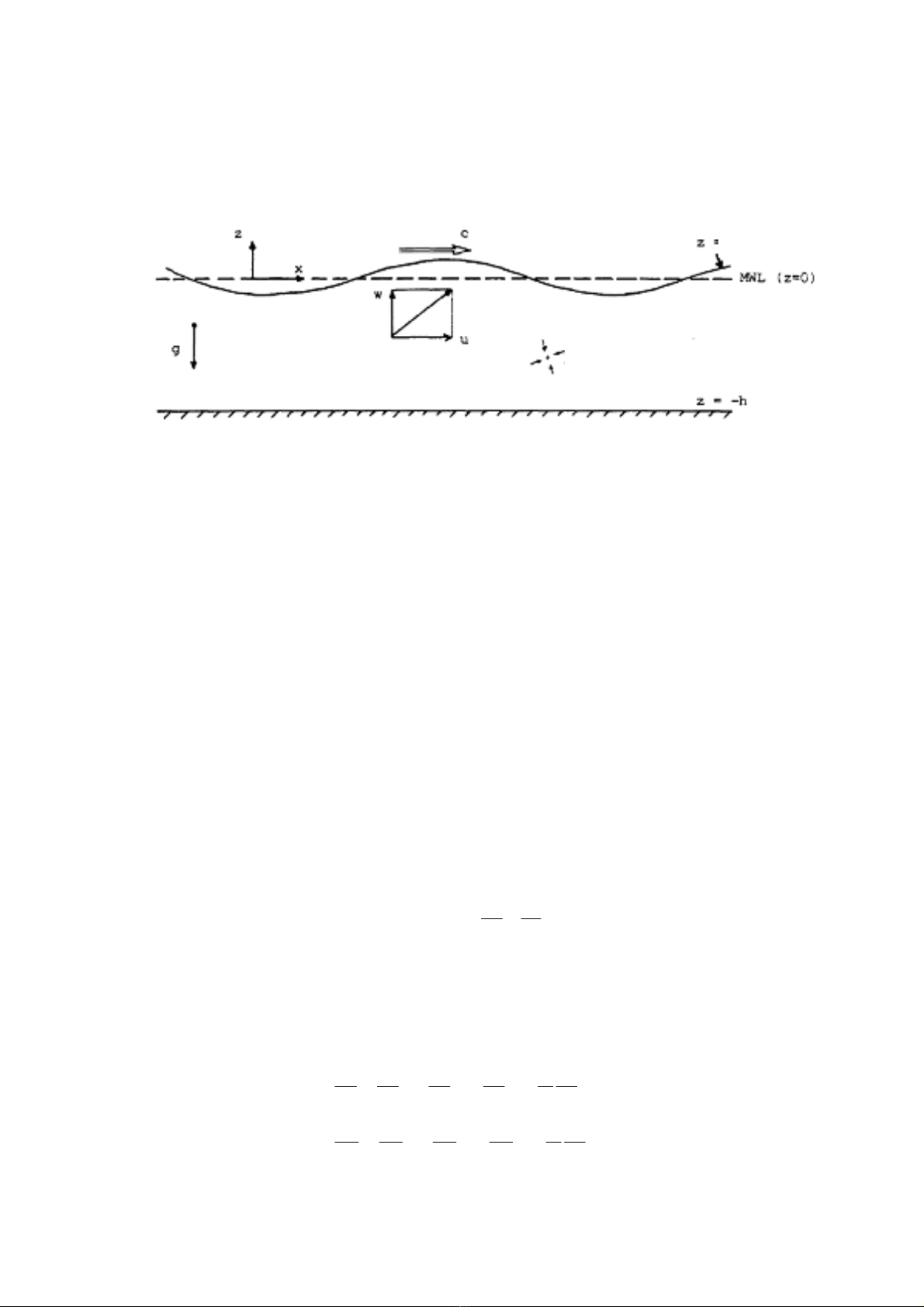
sãng, bµi to¸n biÕn thµnh bµi to¸n hai chiÒu. Nh− vËy, hÖ täa ®é mµ chóng ta chän sÏ gièng
nh− trªn h×nh 3.1.
¸p suÊt p
),( t
x
ζ
H×nh 3.1 HÖ täa ®é vµ c¸c th«ng sè cÇn thiÕt
DÔ dµng t×m ra r»ng víi hÖ täa ®é nµy, ph−¬ng tr×nh m« t¶ bÒ mÆt tù do khi cã mét
sãng truyÒn theo h−íng trôc x víi tèc ®é truyÒn sãng c cã thÓ ®−îc viÕt nh− sau:
(
)
ctxz
−
=
ζ
(3.1)
Mèi liªn hÖ gi÷a b−íc sãng, vËn tèc truyÒn sãng vµ chu kú cã thÓ ®−îc viÕt nh− sau:
cTL
=
(3.2)
C¸c biÕn phô thuéc m« t¶ tr−êng dßng ch¶y khi cã sãng lµ c¸c thµnh phÇn vËn tèc
dßng ch¶y theo c¸c trôc x vµ z vµ ¸p suÊt. C¸c biÕn nµy lÇn l−ît ®−îc ký hiÖu lÇn l−ît lµ u,
w vµ p.
3.1.2 §iÒu kiÖn kh«ng nÐn ®−îc – Ph−¬ng tr×nh liªn tôc
Nh− ®· chØ ra, bµi to¸n ®−îc xem xÐt cã thÓ coi lµ bµi to¸n hai chiÒu. Trong tr−êng
hîp nµy, nh− ®· chØ ra trong ch−¬ng 2 (ph−¬ng tr×nh 2.34), ®iÒu kiÖn kh«ng nÐn ®−îc cña
chÊt láng dÉn ®Õn ph−¬ng tr×nh liªn tôc cã d¹ng sau:
0=
∂
∂
+
∂
∂
y
v
x
u (3.3)
3.1.3 C¸c ph−¬ng tr×nh ®éng l−îng
Víi c¸c gi¶ thiÕt trong phÇn (3.1.1), ph−¬ng tr×nh ®éng l−îng cho chuyÓn ®éng hai
chiÒu cña chÊt láng (c¸c ph−¬ng tr×nh 2.35) khi cã sãng cã thÓ ®−îc viÕt nh− sau:
x
p
z
u
w
x
u
u
t
u
dt
du
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
=
ρ
1 (3.4)
g
z
p
z
w
w
x
w
u
t
w
dt
dw −
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
=
ρ
1 (3.5)
C¸c ph−¬ng tr×nh (3.4) vµ (3.5) kh«ng ®èi xøng v× cã sù xuÊt hiÖn cña g trong (3.5).
22
Hai ph−¬ng tr×nh nµy cã thÓ viÕt d−íi d¹ng t−¬ng tù b»ng c¸ch thÕ
()
)
gzzg ∂∂= /
vµo (3.5) vµ céng thªm mét ®¹i l−îng b»ng kh«ng
(
)
)
gzx
∂
∂
/ vµo (3.4). ViÖc nµy cho ta
mét ph−¬ng tr×nh ®èi xøng:
0=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂gz
p
xz
u
w
x
u
u
t
u
ρ
(3.6)
vµ:
0=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂gz
p
zz
w
w
x
w
u
t
w
ρ
(3.7)
V× sãng lµ sãng hai chiÒu, chóng ta chØ ®−a ra c¸c ®iÒu kiÖn biªn t¹i mÆt tho¸ng vµ t¹i
®¸y. §iÒu kiÖn ®éng häc cho chÊt láng kh«ng nhít chØ ra r»ng kh«ng cã h¹t láng nµo
xuyªn qua bÒ mÆt bao bäc chÊt láng. §iÒu nµy dÉn tíi c¸c ph−¬ng tr×nh sau:
0
=
w t¹i hz
−
=
(3.8)
vµ:
dt
d
w
ζ
= t¹i
(
)
txz ,
ζ
=
(3.9)
Ph−¬ng tr×nh (3.9) cã thÓ khai triÓn thµnh:
x
u
t
w∂
∂
+
∂
∂
=
ζ
ζ
t¹i
(
)
txz ,
ζ
=
(3.10)
§iÒu kiÖn biªn ®éng lùc liªn quan tíi øng suÊt. Bëi v× ®¸y lµ cøng nªn kh«ng mét
®iÒu kiÖn biªn nµo cÇn thiÕt t¹i ®¸y. §iÒu kiÖn kh«ng cã øng suÊt t¹i mÆt tho¸ng cho ta:
0
=
p t¹i
)
txz ,
ζ
=
(3.11)
§iÒu kiÖn lµ øng suÊt c¾t b»ng kh«ng t¹i mÆt tho¸ng kh«ng cÇn ®−a ra ë ®©y v× chÊt
láng ®−îc gi¶ thiÕt lµ kh«ng nhít, vµ nh− vËy øng suÊt c¾t b»ng kh«ng t¹i tÊt c¶ mäi n¬i.
Nh− ®· chØ ra trong ch−¬ng 2, c−êng ®é xo¸y cña mét chÊt láng lý t−ëng b»ng h»ng
sè. Nh− vËy, chuyÓn ®éng b¾t ®Çu kh«ng cã xo¸y sÏ m·i m·i kh«ng xo¸y.
§èi víi mét chÊt láng thùc khi cã sãng, c¸c xo¸y cã thÓ ®−îc t¹o thµnh trong líp biªn
do sãng. Tuy nhiªn, ngo¹i trõ ®íi sãng vì, ®é dµy cña líp biªn khi cã sãng lµ rÊt nhá. Bªn
ngoµi líp biªn máng nµy, dßng ch¶y do sãng t¹o nªn cã thÓ coi lµ kh«ng xo¸y.
Nh− ®· chØ ra trong ch−¬ng 2, ®iÒu kiÖn kh«ng xo¸y ®¶m b¶o sù tån t¹i cña mét thÕ
vËn tèc tháa m·n ph−¬ng tr×nh Laplace: Φ
0
2
2
2
2
=
∂
Φ∂
+
∂
Φ∂
z
x
(3.12)
Trong tr−êng hîp nµy, ta cã thÓ ®−a hµm f(t) trong vÕ ph¶i cña ph−¬ng tr×nh Bernoulli
(2.43) vµo trong thÕ vËn tèc mµ kh«ng ®¸nh mÊt tÝnh tæng qu¸t cña bµi to¸n. Nh− vËy,
ph−¬ng tr×nh Bernoulli (2.43) trë thµnh:
23
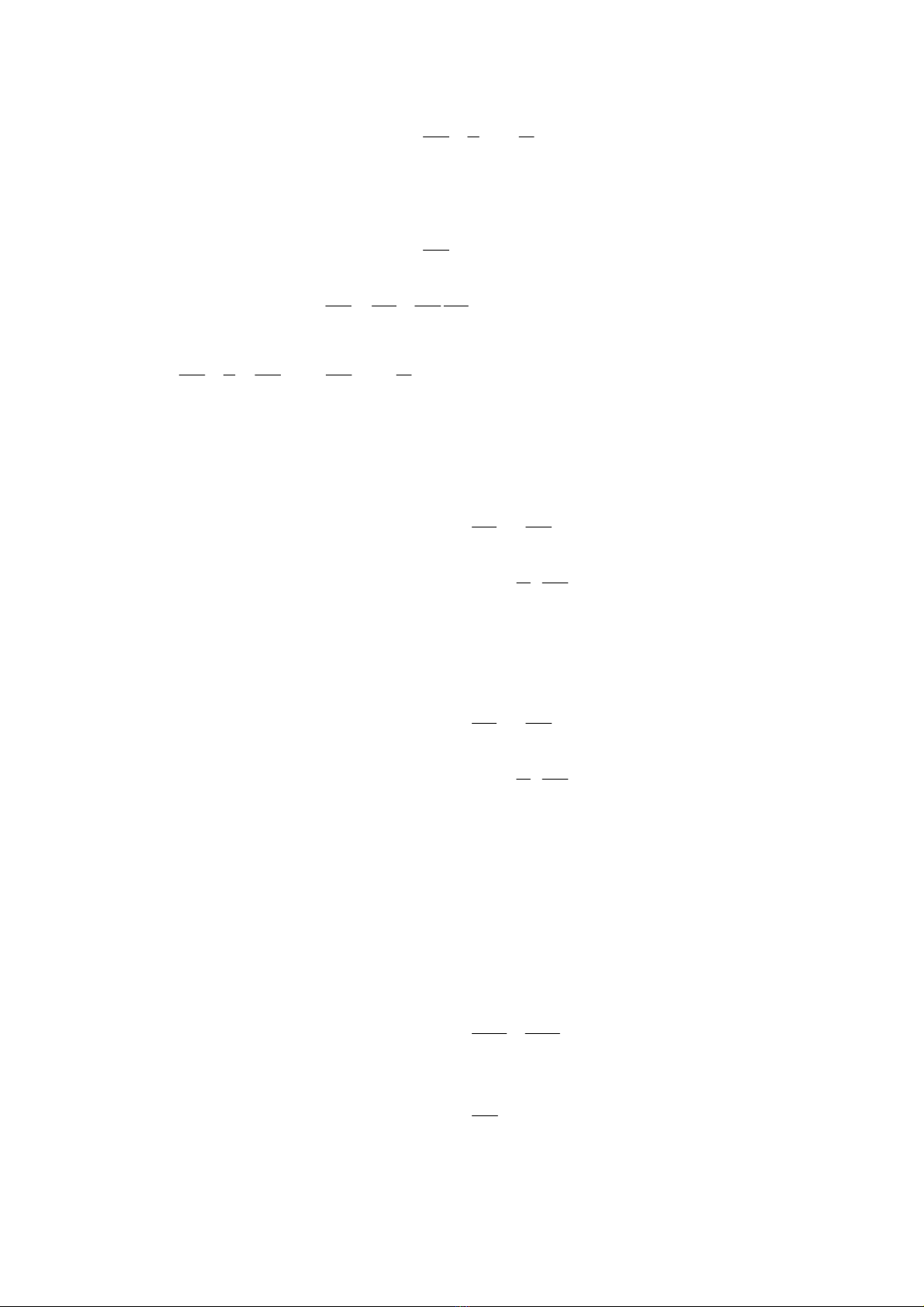
0
2
12=+++
∂
Φ
∂
gz
p
u
t
ρ
(3.13)
Víi thÕ vËn tèc, c¸c ph−¬ng tr×nh ®iÒu kiÖn biªn cho dßng ch¶y khi cã sãng ((3.8),
(3.10) vµ (3.13)) trë thµnh:
0=
∂
Φ
∂
z t¹i hz
−
=
(3.14)
xxtz ∂
∂
∂
Φ
∂
+
∂
∂
=
∂
Φ∂
ζ
ζ
t¹i
(
)
txz ,
ζ
=
(3.15)
0
2
122
=++
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
+
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
+
∂
Φ∂ gz
p
zxt
ρ
t¹i
(
)
txz ,
ζ
=
(3.16)
§ång thêi, ta tuyÕn tÝnh hãa c¸c ph−¬ng tr×nh (3.15) vµ (3.16) b»ng c¸ch bá qua c¸c
sè h¹ng bËc hai, tøc lµ vµ , vµ c¸c ®iÒu kiÖn biªn ®éng lùc trªn bÒ mÆt (3.15) vµ
(3.16) cho ta c¸c ®iÒu kiÖn biªn sau ®©y:
2
u2
v
ζ
ζ
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
=
∂
∂
z
zt (3.17)
ζ
ζ
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
−=
z
tg
1 (3.18)
§Ó cã thÓ sö dông c¸c ®iÒu kiÖn biªn nµy, cÇn ph¶i gi¶ thiÕt thªm lµ biªn ®é cña c¸c
sãng lµ ®ñ nhá ®Ó c¸c ph−¬ng tr×nh (3.17) vµ (3.18) cã thÓ ®−îc ®¬n gi¶n hãa thµnh c¸c
®iÒu kiÖn biªn:
0=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
=
∂
∂
z
zt
ζ
(3.19)
0
1
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
−=
z
tg
ζ
(3.20)
Cïng víi c¸c ®iÒu kiÖn biªn (3.14), (3.19) vµ (3.20), cÇn ph¶i chó ý r»ng nghiÖm vËt
lý cña bµi to¸n truyÒn sãng ph¶i lµ ®iÒu hßa c¶ theo biÕn kh«ng gian x vµ thêi gian t.
3.2 Lêi gi¶i gi¶i tÝch cña bµi to¸n sãng träng lùc bÒ mÆt
Bµi to¸n biªn hoµn chØnh cho sãng träng lùc bÒ mÆt cã thÓ ®−îc ph¸t biÓu l¹i nh− sau.
Ph−¬ng tr×nh vi ph©n:
0
2
2
2
2
=
∂
Φ∂
+
∂
Φ∂
z
x
(3.21)
víi c¸c ®iÒu kiÖn biªn:
0=
∂
Φ
∂
z t¹i hz
−
=
(3.22)
24
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
=
∂
∂
zt
ζ
t¹i 0
=
z (3.23)
⎟
⎠
⎞
⎜
⎝
⎛
∂
Φ∂
−= tg
1
ζ
t¹i 0
=
z (3.24)
§Ó gi¶i bµi to¸n nµy víi c¸c ®iÒu kiÖn biªn, ta gi¶ thiÕt r»ng thÕ vËn tèc cã thÓ ®−îc
biÓu thÞ nh− sau:
(
)
)
(
)
)
tTzZxXtzx
=
Φ
,, (3.25)
Víi X, Z vµ T lÇn l−ît lµ c¸c hµm chØ cña c¸c biÕn sè x, z vµ t.
ThÕ (3.25) vµo (3.21), chóng ta cã:
2
""
k
Z
Z
X
X−=−= (3.26)
víi dÊu phÈy kÐp biÓu thÞ ®¹o hµm bËc hai vµ lµ mét h»ng sè. KÕt qu¶ lµ ta cã hai
ph−¬ng tr×nh vi ph©n th−êng:
2
k
0" 2=+ XkX (3.27)
0" 2=− ZkZ (3.28)
NghiÖm cña (3.27) vµ (3.28) lµ kxDkxBX sincos
+
=
vµ bvíi B,
D, E vµ G lµ c¸c h»ng sè tÝch ph©n. Nh− vËy, nghiÖm cã thÓ viÕt d−íi d¹ng:
kzkz GeEeZ −
+=
()( )
(
)
(
)
tTGeEekxDkxBtzx kzkz −
++=Φ sincos,, (3.29)
Tõ quan ®iÓm vËt lý, ta cã thÓ thÊy r»ng ®èi víi sãng ®¬n, nghiÖm nhÊt thiÕt ph¶i lµ
hµm tuÇn hoµn ®¬n gi¶n cña biÕn thêi gian. Nh− vËy, cã thÓ biÓu thÞ T(t) b»ng c¸c hµm
t cos
ω
hay t sin
ω
.
Cã bèn tæ hîp ®éc lËp cña c¸c sè h¹ng tháa m·n ®iÒu kiÖn tuÇn hoµn c¶ víi x vµ t vµ
lµ nghiÖm cña ph−¬ng tr×nh Laplace lµ:
tkxzZA coscos)(
11
ω
=
Φ
(3.30)
tkxzZA sinsin)(
22
ω
=
Φ
(3.31)
tkxzZA cossin)(
33
ω
=
Φ
(3.32)
sincos)(
44 tkxzZA
ω
=
Φ
(3.33)
TriÓn khai nghiÖm d−íi d¹ng nµy cho phÐp ta t×m gi¸ trÞ cña c¸c h»ng sè tÝch ph©n.
Bëi v× ph−ong tr×nh Laplace lµ tuyÕn tÝnh, mét tæ hîp thÝch hîp cña c¸c nghiÖm nµy sÏ tháa
m·n c¶ ph−¬ng tr×nh Laplace vµ c¸c ®iÒu kiÖn biªn.
C¸c ®iÒu kiÖn biªn (3.22) vµ (3.24) b©y giê sÏ ®−îc ¸p dông cho nghiÖm (3.30). Tõ
(3.30),
(
)
tkxGeEekAz kzkz
ω
coscos/ 11
−
−=∂Φ∂ .
¸p dông ®iÒu kiÖn 0/
1
=
∂Φ∂ z t¹i hz
−
=
cho ta . V× vËy:
khkh GeEe =
−
25