
Tuyển tập Hội nghị Khoa học thường niên năm 2017. ISBN: 978-604-82-2274-1
478
LÝ THUYẾT SÓNG SPIN TUYẾN TÍNH CHO MÔ HÌNH HEISENBERG
TRÊN MẠNG TỔ ONG TRONG BIỂU DIỄN FERMION
Phạm Thị Thanh Nga
Trường Đại học Thủy lợi, email: nga_ptt@tlu.edu.vn
1. GIỚI THIỆU CHUNG
Sau các phát hiện gốm siêu dẫn nhiệt độ
cao và siêu dẫn trên các hợp chất chứa sắt,
tính chất từ của các vật liệu có cấu trúc lớp
đang thu hút sự quan tâm rất lớn của các nhà
vật lý. Ngoài các mạng cấu trúc hình vuông
đặc trưng cho các vật liệu siêu dẫn, mạng tổ
ong trong thời gian gần đây cũng đang được
quan tâm đặc biệt, do các tính chất chuyển
pha tô pô có liên quan tới kích thích từ và
kích thích mật độ điện tích. Tuy đã có nhiều
các công trình lý thuyết nghiên cứu tính chất
từ trên mạng tổ ong, tuy nhiên các kết quả
thu được chưa thể giải thích một cách thỏa
đáng các kết quả thực nghiệm, cũng như đôi
khi lại khác xa nhau. Có thể kể ra hai khó
khăn chính khi nghiên cứu từ tính của mạng
tổ ong. Một là, để nghiên cứu các hệ mô men
từ định xứ người ta thường xuất phát từ
Hamiltonian Heisenberg có dạng sau:
ij i j ij
ij
H J S .S (J 0 )
(1)
trong đó Jij là tương tác trao đổi có bản chất
là tương tác tĩnh điện Coulomb có chú ý tới
nguyên lý Pauli. i
S
là các toán tử véc tơ thỏa
mãn hệ thức giao hoán của các mô men động
lượng: ij ij i
S,S i S
, trong đó ij
là kí
hiệu delta Cronecker còn
là ten xơ hạng
hai phản xứng hoàn toàn. Như vậy các toán tử
spin không phải là toán tử chính tắc, nghĩa là
không thỏa mãn các hệ thức giao hoán (phản
giao hoán) kiểu: i, j ij
aa
. Đây chính là
nguồn gốc của các khó khăn khi nghiên cứu
mô hình Heisenberg (1), bởi vì lúc này ta
không thể áp dụng các kỹ thuật nhiễu loạn
hiện đại của lý thuyết trường lượng tử. Một
trong các phương pháp để khắc phục khó khăn
này là biểu diễn các toán tử spin qua các toán
tử chính tắc boson hoặc fermion. Tuy nhiên,
khi biểu diễn qua các toán tử mới này thì các
trạng thái phi vật lý xuất hiện và người ta phải
áp đặt các điều kiện ràng buộc để loại trừ các
trạng thái phi vật lý (đây là nguyên nhân các
boson hoặc fermion này được gọi là bị “cầm
tù” (slave)). Việc xử lý các điều kiện ràng
buộc thường không dễ dàng và phải tính gần
đúng. Khó khăn thứ hai bắt nguồn từ cấu trúc
của mạng tổ ong. Khác với mạng hình vuông
hoặc mạng tam giác, mạng tổ ong là mạng hai
thành phần (bipartite) trong đó có hai loại
nguyên tử không tương đương nhau về mặt
tương tác với các nguyên tử lân cận (xem
phần dưới đây). Như vậy mạng tổ ong không
phải là mạng Bravais và là mạng có hai
nguyên tử trên một ô cơ sở. Do vậy so với các
mạng hình vuông và mạng tam giác, tính toán
sẽ phức tạp hơn và nhiều khi không có lời giải
giải tích. Trong báo cáo này, chúng tôi sẽ
nghiên cứu trật tự từ cho mô hình Heisenberg
phản sắt từ trên mạng tổ ong, dựa trên biểu
diễn fermion mà Popov-Fedotov đề xuất [1].
2. MÔ HÌNH VÀ PHƯƠNG PHÁP NGHIÊN CỨU
Nghiên cứu mô hình Heisenberg (1) trên
mạng tổ ong được mô tả như trên hình 1.
Hình 1. Cấu trúc tinh thể mạng tổ ong

Tuyển tập Hội nghị Khoa học thường niên năm 2017. ISBN: 978-604-82-2274-1
479
Các véc tơ cơ sở của mạng tinh thể là:
12
aa
a 3,3 ; a 3,3
22
(2)
Từ đây suy ra các véc tơ cơ sở của mạng đảo là:
**
12
21 2 1
a1,; a 1,
33 3 3
(3)
Mỗi ô cơ sở gồm hai nguyên tử A và B.
Các véc tơ nối spin trên nút A với nút B là
i(i =1, 2, 3)
12 3
aa
3,1 ; 3,1 ; a 0, 1
22
(4)
Ta chỉ giới hạn tương tác Jij là phản sắt từ
trên các lân cận gần nhất Jij = J > 0. Vì tính
toán khá dài nên chúng tôi chỉ liệt kê các
bước chính sau đây.
1. Tham số hóa trạng thái cơ bản cổ điển
bằng véc tơ trật tự từ Q
và góc i
:
iiiii
S =S cos Qr u sin Qr v
(5)
trong đó u
và v
là các véc tơ đơn vị trực
giao, góc i
đưa vào để phân biệt hai loại
spin trong một ô cơ sở nên có thể chọn i0
nếu i thuộc phân mạng A còn i
nếu i
thuộc phân mạng B. Thay (5) vào (1) ta có
ngay năng lượng trạng thái cơ bản cổ điển:
i
2
cl i
NS
E = J cosQ
2
(6)
Cực tiểu hóa Ecl theo Q
và góc i
ta thu được:
Q,
và 0
(7)
2. Chuyển sang hệ tọa độ định xứ mà ở đó
trục lượng tử z trùng với hướng của mô men từ
tự phát cổ điển. Lúc đó Hamiltonian có dạng:
ij i j
ij
1
H
JQ,SS
2
(8)
trong đó
ij
J
Q,
là các hàm của Q,
và
các véc tơ lân cận i
.
3. Biểu diễn các toán tử spin qua các toán
tử fermion [5]:
2S 1
iii
,1
Saa
(9)
trong đó i
a
và i
a
là các toán tử fermion còn
là ma trận (2S + 1) x (2S + 1) ứng với spin S
(thí dụ nếu S = ½ thì
là ma trận Pauli.)
Có thể thấy với S = ½ thì có hai trạng thái
phi vật lý trong không gian Fock là trạng thái
chân không và trạng thái có hai fermion, còn
với S = 1 thì trạng thái chân không và trạng
thái có ba fermion là các trạng thái phi vật lý.
Để loại bỏ các trạng thái phi vật lý, Popov-
Fedotov đã biểu diễn tổng thống kê Z qua tích
phân phiếm hàm trong trạng thái kết hợp của
các biến phản giao hoán Grassmann ứng với
các toán tử fermion i
a
và i
a
. Sau đó các tác
giả đã đưa vào toán tử chiếu, tương đương với
việc đưa vào một thế hóa học ảo: i/2
cho S = ½ và i/3
cho S=1.
4. Vì Hamiltonian chứa tích 4 toán tử
fermion nên như thông thường ta đưa vào
trường phụ boson i
bằng cách dùng biến đổi
Hubbard-Stratonovich và ta có thể áp dụng
kỹ thuật nhiễu loạn với trường phụ i
.
5. Lý thuyết sóng spin tuyến tính tương
ứng với việc ta dừng lại ở số hạng bậc hai đối
với i
. Nhìn chung các tính toán là khá dài
và không đơn giản nên không đưa vào cụ thể
ở đây, tham khảo [2-4].
3. KẾT QUẢ NGHIÊN CỨU
3.1. Các kết quả giải tích
i) Năng lượng tự do của hệ:
MF
FF F
(10)
trong đó FMF là năng lượng tự do và mo là
mô men từ tự phát trên mỗi nút cho trường
hợp S = ½ như sau:
2
MF o o
F1/2m1/ln2coshm/2
(11)
oo
m 1 / 2 Tanh m / 2
(12)
với 3J
và F
là bổ chính do thăng giáng cho
năng lượng tự do:
z
z
FF F
, trong đó:
o
pBZ
pm
Flnshlnsh
2
22
(13)
zz
o
pBZ
1
FlnAp
(14)
với phổ magnon:
1/ 2
2
o
pm1 p
(15)
ii
i
ip
p1/3e
(16)
22
2
zz
o2
A
p1K 3J p
(17)
z
z2
2o
1
K14m
4
nếu i
2
(18a)
Tuyển tập Hội nghị Khoa học thường niên năm 2017. ISBN: 978-604-82-2274-1
480
z
z2
2o
1
K14m
8
nếu
0 (18b)
ii) Mô men từ tự phát:
z
z
o
mm m m
(19)
trong đó, mo là mô men từ tự phát trên mỗi
nút cho trường hợp S = ½ cho bởi (12) và m
là bổ chính do thăng giáng cho mô men từ tự
phát:
z
z
mm m
, trong đó:
o
o
o
p
1
m13Jm
4m
11
3J m p
2N p
(20)
zz 2
2
2
0zz
2
K
mp1p
13JK
; (21)
zz
po
11
mCp,
NA
(22)
2
2
zz
2
oo
oo
Cp 2K 3J p Dp
2m m , = i /2
Dp mm, = 0
(23)
3.2. Khảo sát số
i) Nhiệt độ chuyển pha ở gần đúng trường
trung bình:
Nếu ta lấy giới hạn o
m 0 ta sẽ thu được
nhiệt độ chuyển pha thuận từ - phản sắt từ:
C
T3J/4 (ràng buộc chính xác – đường nét liền
trong hình 2) trong khi với 0
(ràng buộc lấy
gần đúng - đường nét đứt trong hình 2) thì
C
T3J/8
. Tức là với S = ½ thì CC
T/T 2
[3].
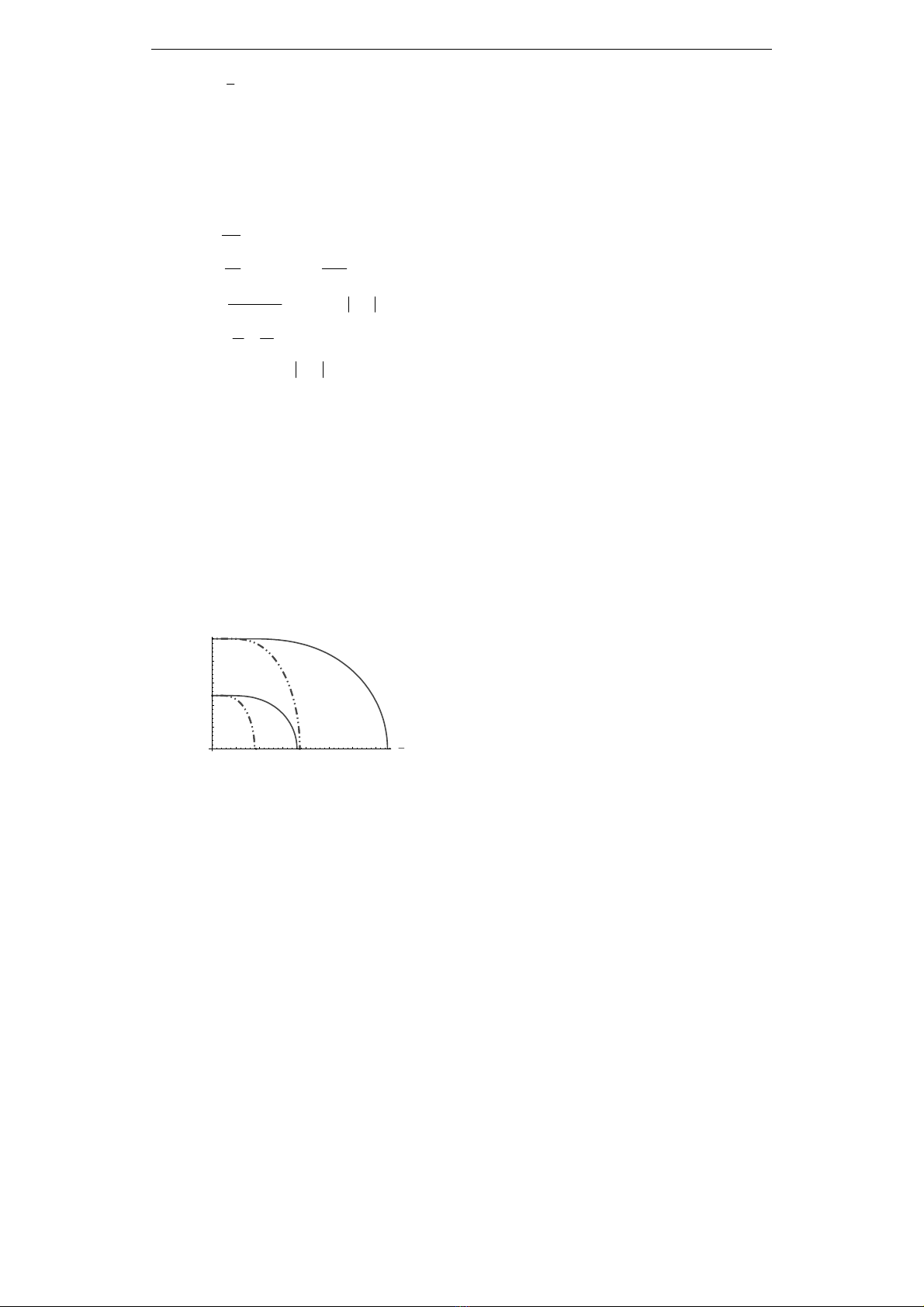
0.1 0.2 0.3 0.4 0.5 0.6 0.7
T
J
0.1
0.2
0.3
0.4
0.5
m
m
o
Hình 2. Đồ thị độ từ hóa tự phát phụ thuộc
nhiệt độ trong gần đúng trường trung bình
(mo – hai đường phía trên) và khi tính thăng
giáng (m - hai đường phía dưới) tương ứng khi
tính điều kiện ràng buộc chính xác (đường nét
liền) và khi tính điều kiện ràng buộc gần đúng
(đường nét đứt).
ii) Năng lượng trạng thái cơ bản có kể đến
thăng giáng với S = ½:
zz
gr T 0 K MF
lim F F F 0,5488
ii) Mô men từ tự phát mo ở gần đúng trường
trung bình với S = ½ (ứng với đồ thị hình 2, hai
đường phía trên, ta có:
o
mT 0K 0,5) và
mô men từ tự phát m khi tính tới bổ chính do
thăng giáng với S = ½ (ứng với đồ thị hình 2,
hai đường phía dưới, ta có:
zz
T0K o
m T 0K lim m m m 0,2418 )
Kết quả chỉ ra phương pháp Popov-Fedotov
áp dụng trong bài báo cáo cho thấy ảnh hưởng
do thăng giáng ở vùng nhiệt độ T 0Kkhác
biệt đáng kể so với các phương pháp khác [2, 3].
4. KẾT LUẬN
Kết luận chính của báo cáo này là:
i) Đã thu được biểu thức tường minh của
năng lượng tự do và độ từ hoá trên mỗi nút khi
chú ý tới ảnh hưởng của thăng giáng spin trong
lý thuyết sóng spin tuyến tính bằng phương
pháp tích phân phiếm hàm Popov-Fedotov.
ii) Phân tích kết quả cho độ từ hóa tự phát ở
gần đúng trường trung bình cho thấy khi tính
chính xác điều kiện ràng buộc sẽ cho nhiệt độ
chuyển pha tăng 2 lần so với các lý thuyết khác.
Điều này phù hợp với các lý giải vật lý [3, 4].
iii) Khảo sát số cho mô men từ tự phát cho
thấy ở vùng nhiệt độ T 0K khi tính đến điều
kiện ràng buộc chính xác, kết quả số có sự
khác biệt đáng kể so với khi ta tính điều kiện
ràng buộc gần đúng.
5. TÀI LIỆU THAM KHẢO
[1] Popov V. N. and Fedotov S. A. 1988.
“Functional integration method and diagram
technique for spin systems”. Sov. Phys. JETP
67, 535.
[2] Dillenschneider R. And Richert J. 2006.
“Site occupation constraint in mean-field
approaches of quantum spin systems at
finite temperature”. Phys. Rev. B 73,
024409.
[3] Nga P. T. T. and Thang N. T. 2012. “Néel
state in the fermionized spin ½ Heisenberg
antiferromagnet on the hypercubic and
triangular lattices”. Comm. in Phys.
22 and Erratum, Communications in
Physics 22, No 4.
[4] Nga P. T. T. and Thang N. T. 2017. “Magnetic
order of spin S = 1 antiferromagnetic”. Journal
of Physics: Conf. Series 865 012015./.











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














