Ch−¬ng 4 nh÷ng lý thuyÕt sãng phi tuyÕn cho
vïng cã ®é s©u kh«ng ®æi
4.1 Giíi thiÖu chung
Kh«ng cã mét lêi gi¶i chÝnh x¸c nµo cho c¸c ph−¬ng tr×nh ®Çy ®ñ vÒ sãng ®−îc tr×nh
bµy trong ch−¬ng 3. §iÒu nµy lµ do c¸c sè h¹ng phi tuyÕn trong c¸c ®iÒu kiÖn biªn trªn bÒ
mÆt tù do. Trong c¸c xÊp xØ tuyÕn tÝnh, c¸c sè h¹ng nµy bÞ bá qua hoµn toµn. Tuy nhiªn,
trong c¸c lý thuyÕt phi tuyÕn th× chóng ®−îc tÝnh ®Õn b»ng c¸ch xÊp xØ. RÊt nhiÒu lý thuyÕt
vÒ sãng phi tuyÕn víi ph−¬ng ph¸p gi¶i quyÕt vµ møc ®é chÝnh x¸c cña viÖc xÊp xØ kh¸c
nhau ®· ®−îc ®−a ra. Trong ch−¬ng nµy, ta sÏ tr×nh bµy mét c¸ch ®Þnh tÝnh tæng quan vÒ
nh÷ng lý thuyÕt nµy.
Lý thuyÕt sãng phi tuyÕn ®Çu tiªn do Stokes (1847) ®−a ra. Lý thuyÕt cña «ng vÒ mÆt
nguyªn t¾c lµ cã thÓ ¸p dông cho tÊt c¶ c¸c ®é s©u. Tuy nhiªn, trong thùc tÕ, ®èi víi n−íc
n«ng th× kÕt qu¶ lý thuyÕt nµy chØ chÊp nhËn ®−îc khi mµ ®é cao sãng rÊt nhá. Mét lo¹i lý
thuyÕt thø hai lµ chØ ¸p dông cho c¸c ®iÒu kiÖn sãng n−íc n«ng. Nh÷ng lý thuyÕt nµy sÏ
®−îc tr×nh bµy trong môc 4.3.
C¸c lý thuyÕt võa nãi cho ta c¸c biÓu thøc gi¶i tÝch vÒ nhiÒu hÖ sè cÇn thiÕt cho viÖc
tÝnh to¸n sãng. C¸c lý thuyÕt sè trÞ cho ta thuËt to¸n ®Ó x¸c ®Þnh gi¸ trÞ cña c¸c hÖ sè cho
mét tËp hîp cho tr−íc c¸c ®iÒu kiÖn ®Çu vµo. Mét sè lý thuyÕt sè trÞ sÏ ®−îc tr×nh bµy trong
môc 4.4. VÊn ®Ò vÒ tÝnh ®óng ®¾n cña c¸c lý thuyÕt sÏ ®−îc xö lý trong môc 4.5.
4.2 Lý thuyÕt Stokes
Stokes (1847) dïng ph−¬ng ph¸p xÊp xØ liªn tiÕp, cã thÓ ®−îc m« t¶ s¬ qua nh− sau.
KÕt qu¶ cña lý thuyÕt tuyÕn tÝnh ®−îc dïng ®Ó t×m mét xÊp xØ thø nhÊt cho c¸c sè h¹ng
phi tuyÕn bÞ bá qua. ViÖc hiÖu chØnh c¸c kÕt qu¶ cña phÐp xÊp xØ thø nhÊt (tuyÕn tÝnh) cña
nghiÖm ®−îc tiÕn hµnh b»ng c¸ch tÝnh ®Õn ®iÒu trªn.
B»ng c¸ch dïng nghiÖm ®· ®−îc hiÖu chØnh lÇn thø nhÊt, mét xÊp xØ lÇn thø hai cho
c¸c sè h¹ng phi tuyÕn ®−îc tiÕn hµnh. Sau ®ã lµ xÊp xØ lÇn thø ba. NÕu nh− qu¸ tr×nh nµy héi
tô th× nã cã thÓ cø ®−îc tiÕp tôc cho ®Õn khi ®¹i l−îng hiÖu chØnh trë nªn ®ñ bÐ. ThËt ra th×
mét giíi h¹n thùc tÕ sÏ ®¹t ®−îc sím mµ kh«ng ph¶i tiÕn hµnh nhiÒu phÐp xÊp xØ v× c¸c biÓu
thøc to¸n häc trë nªn rÊt dµi vµ rÊt khã t×m ra c¸c xÊp xØ bËc cao.
41
Nh− ®· tr×nh bµy ë trªn, c¸c biÓu thøc to¸n häc trong nh÷ng xÊp xØ bËc cao rÊt dµi. Bëi
vËy, ®Ó dÔ dµng h¬n trong viÖc ¸p dông nh÷ng lý thuyÕt nµy, ng−êi ta ®· chuÈn bÞ nh÷ng ®å
thÞ vµ b¶ng nh− lµ nh÷ng ®å thÞ vµ b¶ng cña Skjelbreia (1959) cho xÊp xØ bËc 3, trong ®ã tÊt
c¶ nh÷ng sè h¹ng cã bËc 3 hay nhá h¬n ®−îc gi÷ nguyªn vµ nh÷ng sè h¹ng kh¸c bÞ bá qua.
Trong phÇn tiÕp theo, mét sè kÕt qu¶ sÏ ®−îc tr×nh bµy chñ yÕu d−íi d¹ng ®Þnh tÝnh.
Mét sè ph−¬ng tr×nh cña lý thuyÕt bËc hai sÏ ®−îc tr×nh bµy víi môc ®Ých diÔn gi¶i.
4.2.1 MÆt c¾t bÒ mÆt n−íc
BiÓu thøc bËc 2 ®èi víi mÆt n−íc cã thÓ ®−îc viÕt nh− sau:
()
SSS sin
ˆ
cos
ˆ
ζζζ
+= 21
1
(4.1)
trong ®ã:
a=
ˆ
ζ
(4.2)
(
)
kh
khkh
ka 2
2
2sinh
2cosh2cosh
2
1
ˆ
+
=
ζ
(4.3)
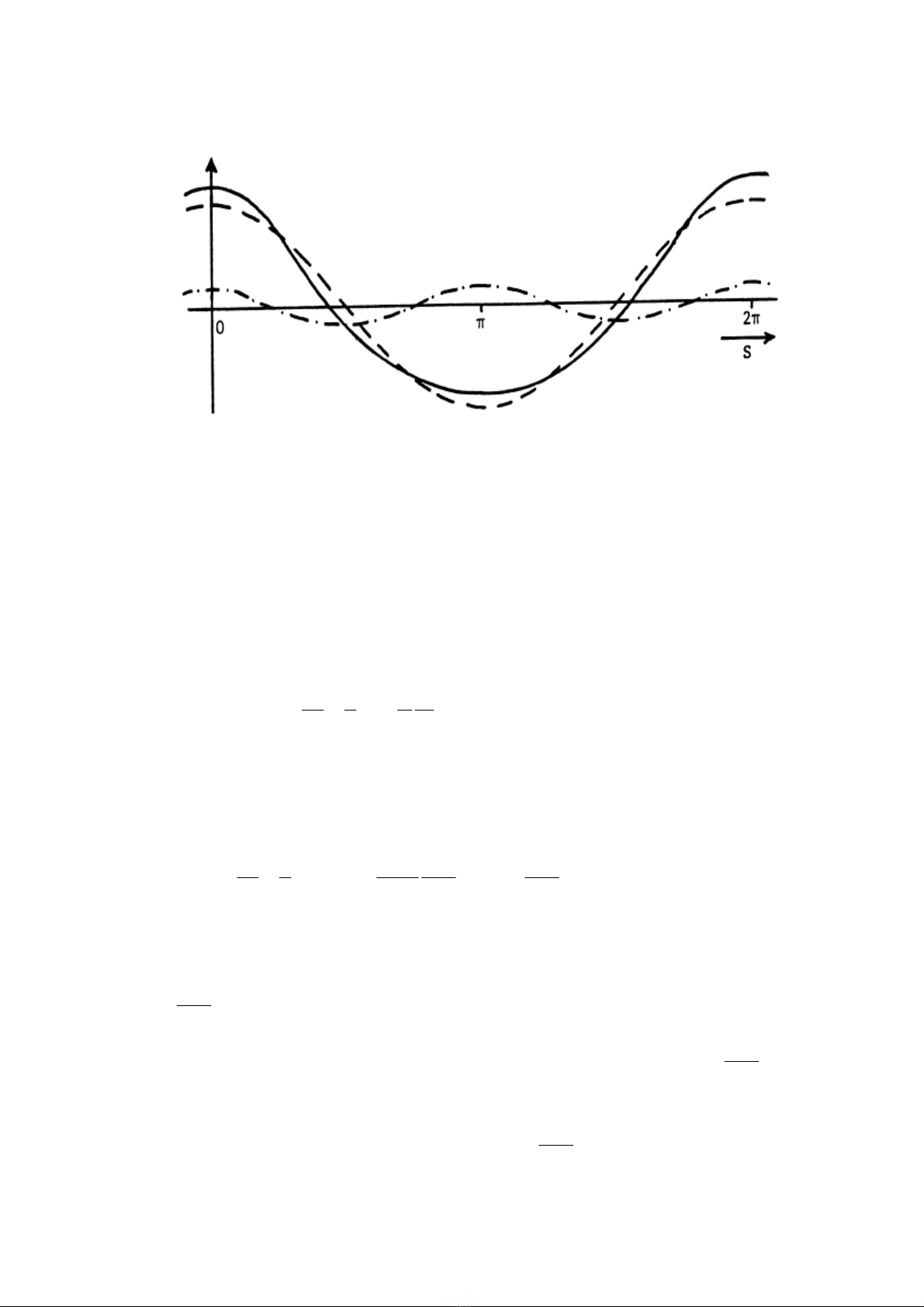
§iÓm S=0 ®−îc chän t¹i mét ®Ønh sãng. H×nh 4.1 tr×nh bµy mét ph¸c th¶o cña (4.1).
Mét sè h¹ng tuyÕn tÝnh ®iÓn h×nh lµ tû lÖ víi hay , trong ®ã a lµ biªn ®é
cña dao ®éng mùc n−íc trong phÐp xÊp xØ tuyÕn tÝnh, vµ
Sa cos Sa sin
(
)
kxtS
−
=
ω
lµ pha. Bëi v× c¸c
thµnh phÇn phi tuyÕn bao gåm c¸c tÝch nh− lµ , xÊp xØ ®Çu tiªn cho c¸c sè h¹ng nµy bao
gåm c¸c sè h¹ng tû lÖ víi
2
u
(
)
(
)
SaSa 2cos12/1cos 222 += , vµ c¸c sè h¹ng t−¬ng tù
víi . §iÒu nµy còng ¸p dông ®−îc cho hiÖu chØnh thø nhÊt cña xÊp xØ tuyÕn tÝnh cña
nghiÖm chÝnh x¸c. TiÕp tôc theo c¸ch nµy, ta cã thÓ t×m ®−îc nh÷ng xÊp xØ liªn tiÕp cña
nghiÖm chÝnh x¸c d−íi d¹ng nh÷ng sè h¹ng liªn tôc cña mét chuçi sè mò cña a (c¸c sè
h¹ng tû lÖ víi a, , , v.v...). NÕu a lµ ®ñ nhá (®èi víi L vµ h), mçi sè h¹ng bËc cao sÏ nhá
h¬n nhiÒu nh÷ng sè h¹ng bËc thÊp h¬n vµ nÕu nh− khi ®ã chuçi ®−îc kÕt thóc b»ng mét mét
vµi sè h¹ng th× ta cã thÓ t×m ®−îc mét xÊp xØ tiÖn lîi.
S
2
sin
2
a3
a
MÆt c¾t sãng d−êng nh− cã c¸c ®Ønh hÑp h¬n vµ nhän h¬n mÆt c¾t biÓu thÞ b»ng hµm
cosine, vµ bông réng h¬n vµ ph¼ng h¬n. HÖ qu¶ lµ mùc n−íc t¹i ®Ønh sãng trªn mùc biÓn
trung b×nh (MWL) cao h¬n mét nöa chiÒu cao sãng, víi gi¸ trÞ v−ît qu¸ lµ (tíi bËc 2).
§iÒu nµy quan träng cho viÖc tÝnh to¸n lùc sãng t¸c ®éng lªn c¸c c«ng tr×nh ë n−íc n«ng
hay lµ cho viÖc x¸c ®Þnh ®é cao cÇn thiÕt cña kho¶ng kh«ng gi÷a mÆt d−íi cña cÇu tµu hay
bÕn mµ mùc MWL (cßn ®−îc gäi lµ “kho¶ng kh«ng”).
2
ˆ
ζ
42
2
ζ
MWL
1
ζ
21
ζ
ζ
+
H×nh 4.1 MÆt c¾t bÒ mÆt n−íc khi cã sãng xÊp xØ b»ng lý thuyÕt bËc 2 cña Stokes
TÝnh bÊt ®èi xøng nh− ë trªn th−êng ®−îc quan s¸t thÊy râ rµng trong c¸c sãng thùc.
MÆt c¾t thùc ®o d−êng nh− ®−îc dù b¸o rÊt tèt b»ng lý thuyÕt Stokes bËc 2 vµ bËc 3 cho sãng
n−íc s©u, nh−ng sù phï hîp lµ kÐm h¬n cho c¸c ®iÒu kiÖn n−íc n«ng. Tõ lý thuyÕt cã thÓ rót
ra mét chØ thÞ cho qu¸ tr×nh nµy, thÝ dô nh− tû sè cña biªn ®é bËc hai vµ biªn ®é bËc nhÊt cÇn
ph¶i nhá ®Ó ph−¬ng ph¸p tiÕp cËn Stokes lµ cã gi¸ trÞ. T¹i n−íc s©u, tû sè nµy lµ (xem c¸c
ph−¬ng tr×nh 4.2 vµ 4.3):
L
H
ka 22
1
ˆ
ˆ
1
2
π
ζ
ζ
≅≅
(
)
1>>kh (4.4)
Tû sè nµy th−êng lµ nhá (lín nhÊt lµ vµo kho¶ng 0.2) v× r»ng sãng vì giíi h¹n ®é dèc
cã thÓ cã cña sãng. MÆt kh¸c t¹i n−íc s©u h¬n tû sè trªn trë thµnh (xem c¸c ph−¬ng tr×nh 4.2
vµ 4.3):
()
3
2
2
3
2
2
3
2
110
32
3
4
3
ˆ
ˆ
h
HL
h
HL
kakh ×≅≅≅ −
−
π
ζ
ζ
(
)
1
<kh (4.5)
NÕu ta yªu cÇu th× bÊt ®¼ng thøc sau sÏ ph¶i ®−îc tháa m·n:
12 ˆ
2.0
ˆ
ζζ
≤
20
3
2
≤
h
HL
§©y lµ mét yªu cÇu rÊt chÆt chÏ vÒ H/L v× r»ng L>>h t¹i n−íc n«ng. Tû sè 3
2
h
HL th−êng
®−îc gäi lµ sè Ursell, ký hiÖu bëi U:
r
3
2
h
HL
Ur= (4.6)
43
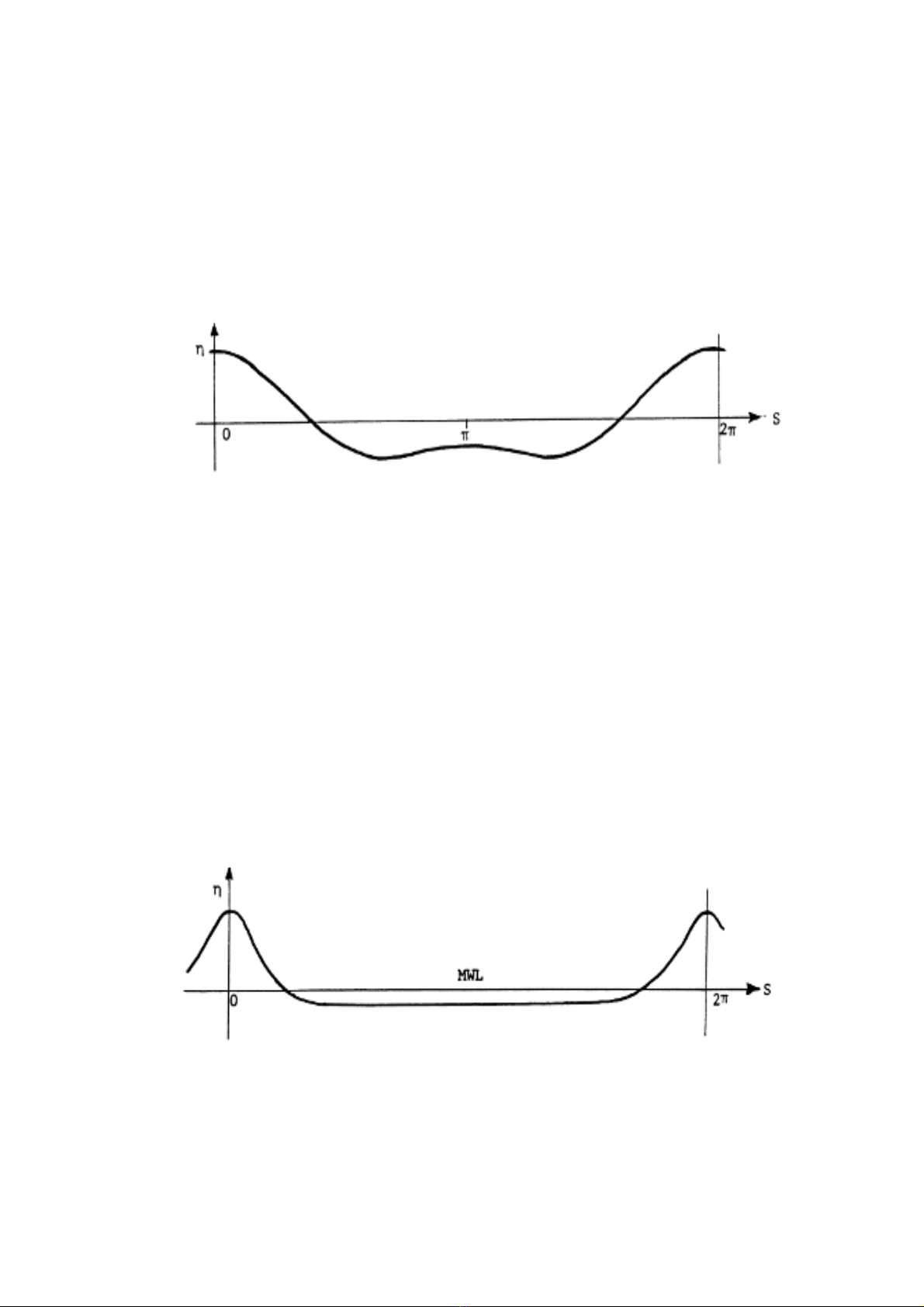
NÕu lµ qu¸ lín th× chuçi Stokes ph©n kú. Mét chØ thÞ cho ®iÒu nµy lµ sù xuÊt hiÖn
cña mét cùc ®¹i thø hai t¹i bông sãng khi mµ nh− ®−îc ph¸c th¶o trªn h×nh Fig.
4.2. Khi mµ cùc ®¹i thø hai t¹i bông sãng kh«ng ®−îc quan tr¾c ë sãng thùc t¹i n−íc n«ng
th× sù xuÊt hiÖn cña nã trong c¸c kÕt qu¶ tÝnh to¸n chØ ra r»ng lý thuyÕt ®−îc sö dông trong
c¸c ®iÒu kiÖn v−ît qu¸ giíi h¹n ¸p dông cña nã.
r
U
4/
ˆˆ
ζζ
>12
H×nh 4.2 Cùc ®¹i thø hai t¹i bông sãng do lý thuyÕt Stokes bËc 2 dù b¸o t¹i n−íc
rÊt n«ng.
C¸c ®o ®¹c mùc n−íc khi cã sãng lín t¹i n−íc n«ng cho thÊy c¸c profile mÆt n−íc víi
bông dµi vµ ph¼ng cïng víi ®Ønh hÑp vµ nhän, nh− chØ ra trªn h×nh 4.3.
NÕu profile nµy ®−îc xÊp xØ b»ng mét tæng c¸c thµnh phÇn ®iÒu hßa d¹ng cosin (cos S,
cos 2S v.v.) th× cÇn cã mét sè l−îng lín c¸c thµnh phÇn. §iÒu nµy cã nghÜa lµ chuçi cÇn ph¶i
®−îc tÝnh t¹i mét bËc rÊt cao. §©y lµ mét nhiÖm vô rÊt khã kh¨n vµ mÊt thêi gian, vµ do vËy
trong thùc tÕ, kh«ng nªn ¸p dông chuçi Stokes trong c¸c ®iÒu kiÖn ®ã, thËm chÝ c¶ khi mµ nã
kh«ng ph©n kú.
H×nh 4.3 Profile mÆt n−íc khi cã sãng ®o ®−îc t¹i n−íc n«ng.
4.2.2 VËn tèc vµ quü ®¹o h¹t n−íc
44
Trong xÊp xØ phi tuyÕn, vËn tèc h¹t n−íc kh«ng cßn lµ ®èi xøng qua gi¸ trÞ trung b×nh
(b»ng 0 nÕu chØ cã sãng). VËn tèc n»m ngang cña h¹t n−íc cã d¹ng bÊt ®èi xøng gÇn gièng
víi mÆt n−íc. V× vËy, vËn tèc cã gi¸ trÞ tuyÖt ®èi lín h¬n bªn d−íi ®Ønh so víi bªn d−íi bông.
§iÒu nµy ¶nh h−ëng m¹nh tíi viÖc tÝnh to¸n ¸p lùc sãng lªn c«ng tr×nh, ®Æc biÖt lµ trong c¸c
®iÒu kiÖn n−íc n«ng. C¸c sè h¹ng bËc cao trong c¸c chuçi vËn tèc h¹t n−íc gi¶m nhanh h¬n
theo kho¶ng c¸ch d−íi bÒ mÆt so víi c¸c sè h¹ng bËc thÊp. VËn tèc ë gÇn ®¸y ®−îc dù b¸o
kh¸ tèt b»ng lý thuyÕt tuyÕn tÝnh.
Trong lý thuyÕt tuyÕn tÝnh, quü ®¹o h¹t n−íc lµ ®èi xøng c¶ theo ph−¬ng ®øng vµ
ph−¬ng ngang. Trong c¸c lý thuyÕt phi tuyÕn, kh«ng thÓ bá qua sù bÊt ®èi xøng cña vËn tèc
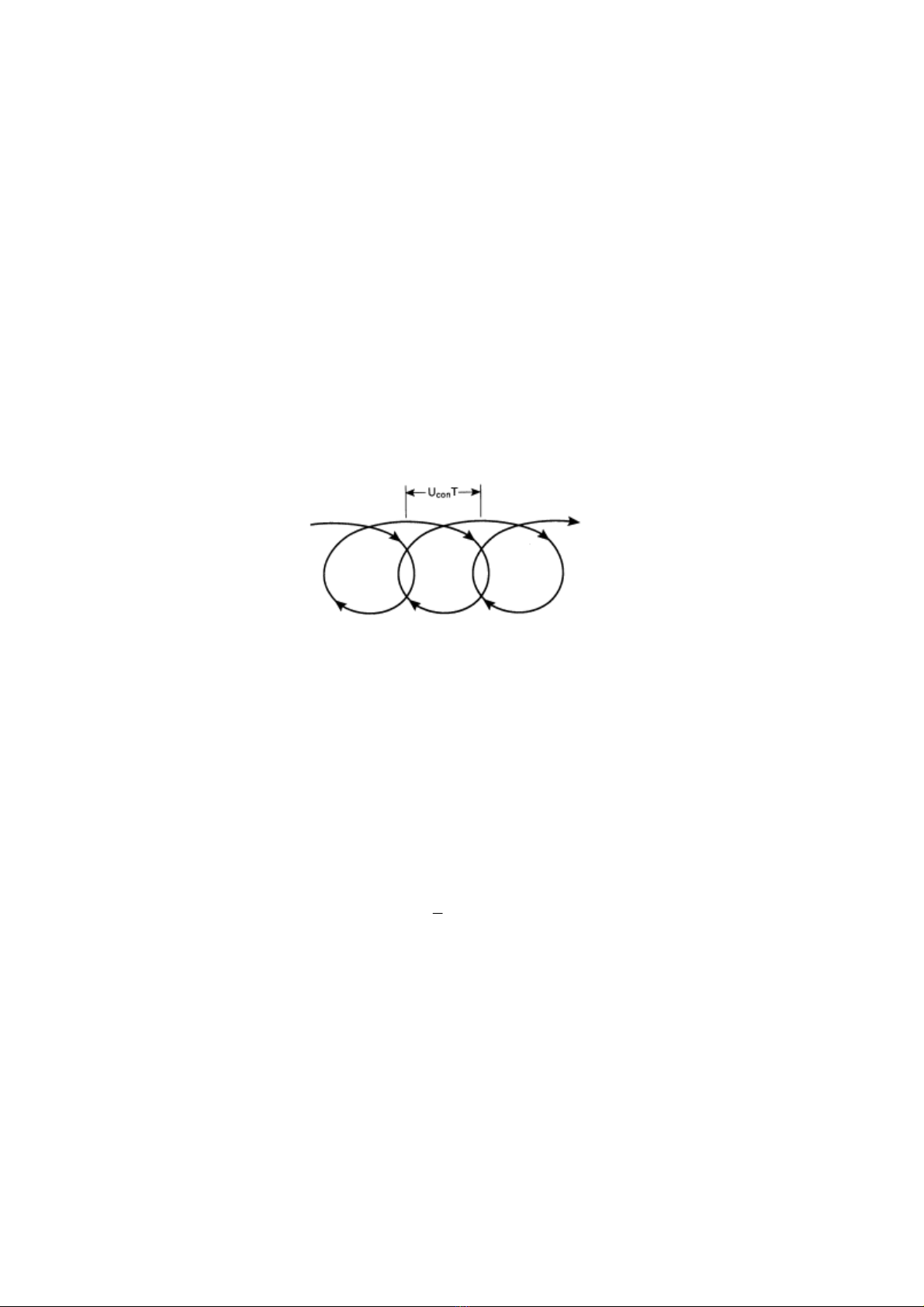
h¹t n−íc. V× vËy quü ®¹o h¹t n−íc kh«ng cßn lµ ®èi xøng. Sau mét chu kú sãng th× h¹t n−íc
tiÕn vÒ phÝa tr−íc mét chót, nh− vÏ trªn h×nh 4.4.
H×nh 4.4 Quü ®¹o h¹t n−íc xÊp xØ b»ng c¸c lý thuyÕt sãng phi tuyÕn
VËy, sãng g©y ra vËn chuyÓn khèi l−îng ®èi víi hÖ quy chiÕu cña ta. Mét c¸ch kh¸c lµ
ta cã thÓ chän mét hÖ quy chiÕu sao cho vËn tèc vËn chuyÓn khèi l−îng tæng céng d− tÝch
ph©n theo ph−¬ng th¼ng ®øng b»ng 0. Trong tr−êng hîp nµy c¸c h¹t n−íc trong phÇn thÊp
cña profile th¼ng ®øng sÏ cã vËn tèc d− ng−îc l¹i vµ chØ cã c¸c h¹t n−íc ë trªn lµ cã vËn tèc
d− theo h−íng sãng. Víi ®é chÝnh x¸c bËc hai, vËn tèc trung b×nh thêi gian cña mét h¹t n−íc
t¹i mét ®é cao trung b×nh trong c¸c ®iÒu kiÖn sãng n−íc s©u ®−îc cho bëi:
0
z
(
)
0
2
0
kz
aekazu
ω
= (4.7)
1>>kh
Víi n−íc trung b×nh vµ n−íc n«ng, lý thuyÕt Stokes cho dù ®o¸n kh«ng chÝnh x¸c vÒ
vËn tèc vËn chuyÓn vËt chÊt. §iÒu nµy lµ do ¶nh h−ëng cña ®é nhít (chØ giíi h¹n trong líp
biªn máng gÇn ®¸y). Longuet-Higgins (1953) ®· ph©n tÝch kü cµng vÒ tèc ®é vËn chuyÓn vËt
chÊt do sãng g©y ra tÝnh theo c¸c lý thuyÕt sãng kh¸c nhau vµ cã tÝnh ®Õn ¶nh h−ëng cña ®é
nhít.
4.2.3 Mèi liªn hÖ ph©n t¸n vµ vËn tèc pha
Trong xÊp xØ Stokes bËc 2, mèi liªn hÖ ph©n t¸n gièng nh− trong lý thuyÕt tuyÕn tÝnh.
45