
339
)12(
2
)14(
cos)
2
(
~
)(
~
)12( )12/(
0
k
N
nN
nxnxkX N
n
(13.8)
Nhưng cos[(2k + 1)] = 2coscos(2k) - cos[(2k - 1) ]. Vì vậy,
)12(
2
)14(
cos)
2
(
~
)(
~
-
2
2
)14(
cos)
2
(
~
)(
~
2)12(
1)2/(
02
)12/(
02
k
N
nN
nxnx
k
N
nN
nxnxkX
N
n
N
n
(13.9)
Biểu thức thứ hai trong (13.9) là X(2k - 1). Bởi vậy, nên (13.9) rút gọn
thành
}
2
2
)14(
cos
2
)14(
cos)
2
(
~
)(
~
2{)12( )12/(
02
k
N
n
N
nN
nxnxkX N
n
)12()12(
2
2
)14(
cos
kXk
N
n
(13.10)
Đặt )
2
(
~
)(
~
)(
00 N
nxnxnx (13.11)
và
N
nN
nxnxx 2
)14(
cos2)
2
(
~
)(
~
01
(13.12)
Vì vậy:
12/
000 )
2
(2
)14(
cos)()2( N
nN
n
nxkX
(13.13)
Và
12/
001 )12()
)
2
(2
)14(
cos()()12( N
n
kX
N
kn
nxkX
(13.14)
Biểu thức (3.13) và (3.14) dẫn chúng ta đến sơ đồ hình 13.4 cho DCT 8
điểm. Chú ý rằng X(1) = X(-1). Biểu thức (13.11) và (13.12) là biểu thức cho
các phép toán bướm:
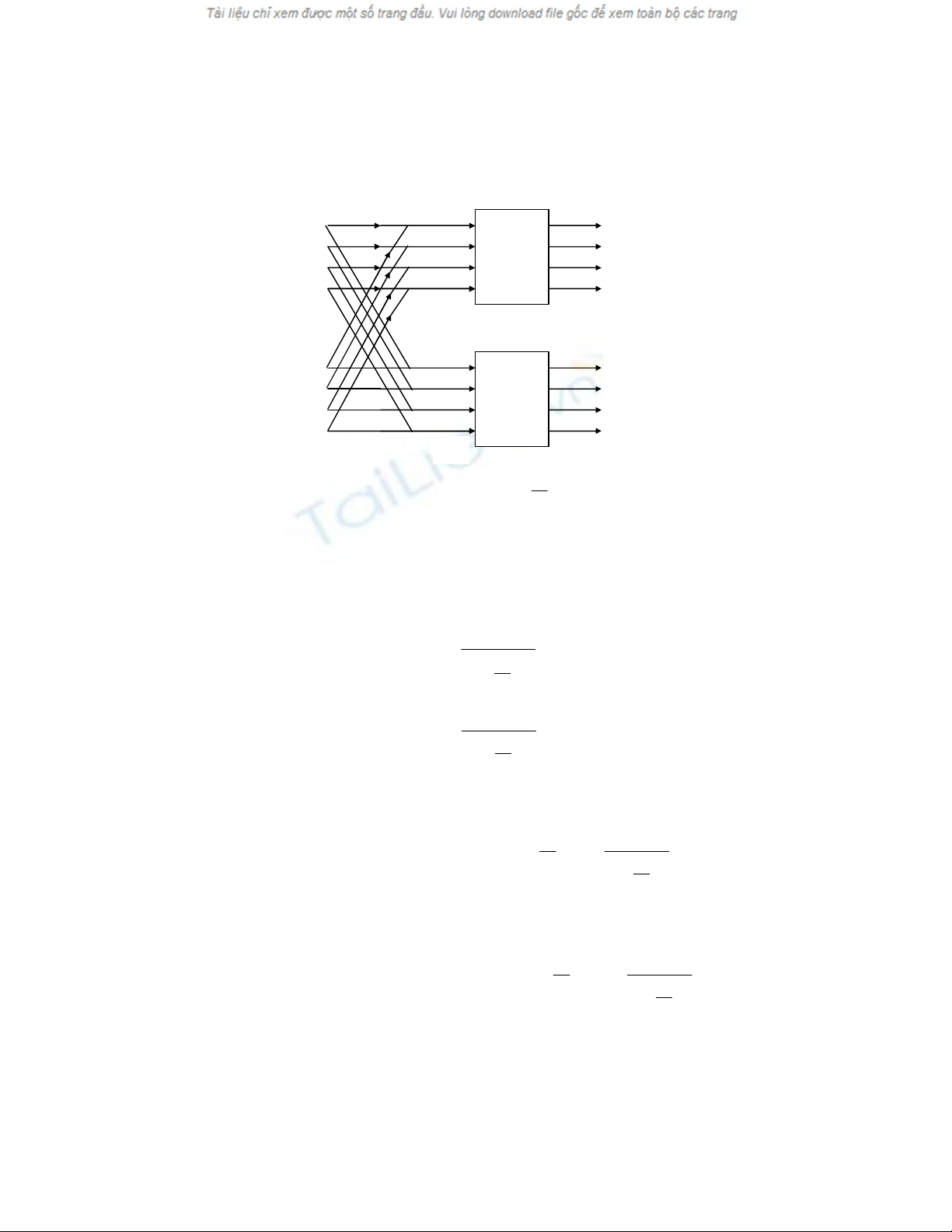
340
Đặt )2()(
00 kXkY
Y k X k X k
01 2 1 2 1( ) ( ) ( )
(13.15)
Hình 13.4 Lưu đồ cho biểu thức (13.13) và (13.14).
Vì thế:
12/
00000
2
2
)14(
cos)()( N
nN
kn
nxkY
(13.16)
12/
00101 )
)
2
(2
)14(
cos()()( N
nN
kn
nxkY
(13.17)
Chia Y00(k) và Y01(k) thành hai dãy chỉ số chẵn và lẻ như trên chúng ta được:
)
2
(2
)14(
cos)
4
()()2( 1)4/(
0000000
N
nN
nN
nxnxkY
(13.18)
1)4/(
0000000 )
2
(2
)14(
cos2)
4
()()12( N
nN
nN
nxnxkY
13
16
2C
9
16
2C
16
2C16
2C
-1
-1
-1
-1
DCT
4 điểm.
x(0)
x(2)
x(4)
x(6)
)0(
~
x
)1(
~
x
)2(
~
x
)3(
~
x
DCT
4 điểm.
2x(1)
x(3)+x(1)
x(5)+x(3)
x(7)+x(5)
)0(
~
x
)1(
~
x
)2(
~
x
)3(
~
x
j
i
Ci
j
cos
341
)12(
)
4
(2
)14(
cos 00
kY
N
kn
s (13.19)
)
2
(2
)14(
cos2)
4
()()2( 1)4/(
0010101
N
nN
nN
nxnxkY
(13.20)
)12(
)
4
(2
)14(
cos
)
2
(2
)14(
cos2)
4
()()12(
01
1)4/(
0010101
kY
N
kn
N
nN
nxnxkY N
n
(13.21)
Đặt )
4
()()( 000010
N
nxnxnx (13.22)
)14(
000011 ))
4
()(()(
n
N
C
N
nxnxnx (13.23)
)
4
()()( 010112 N
nxnxnx (13.24)
)14(
010113 ))
4
()(()(
n
N
C
N
nxnxnx (13.25)
ở đây
j
i
Ci
j
cos (13.26)
-1
-1
-1
-1
2C
5
8X11(
1)
2C
8
X
11
(
DCT
DCT
X00(0
)
X00(1
)
X00(2
)
X00(3
)
Y
00(0
)
Y
00(2
)
2Y00(1
)
Y
00(3)+Y00(1
)
X10(0
)
X
10
(1
)
2C
5
8X13(
1)
2C8X13(
0)
DCT
DCT
X01(0
)
X01(1
)
X01(2
)
X01(3
)
Y
01(0
)
Y
01(2
)
2Y01(1
)
Y
01(3)+Y01(1
)
X12(0
)
X12(1
)

342
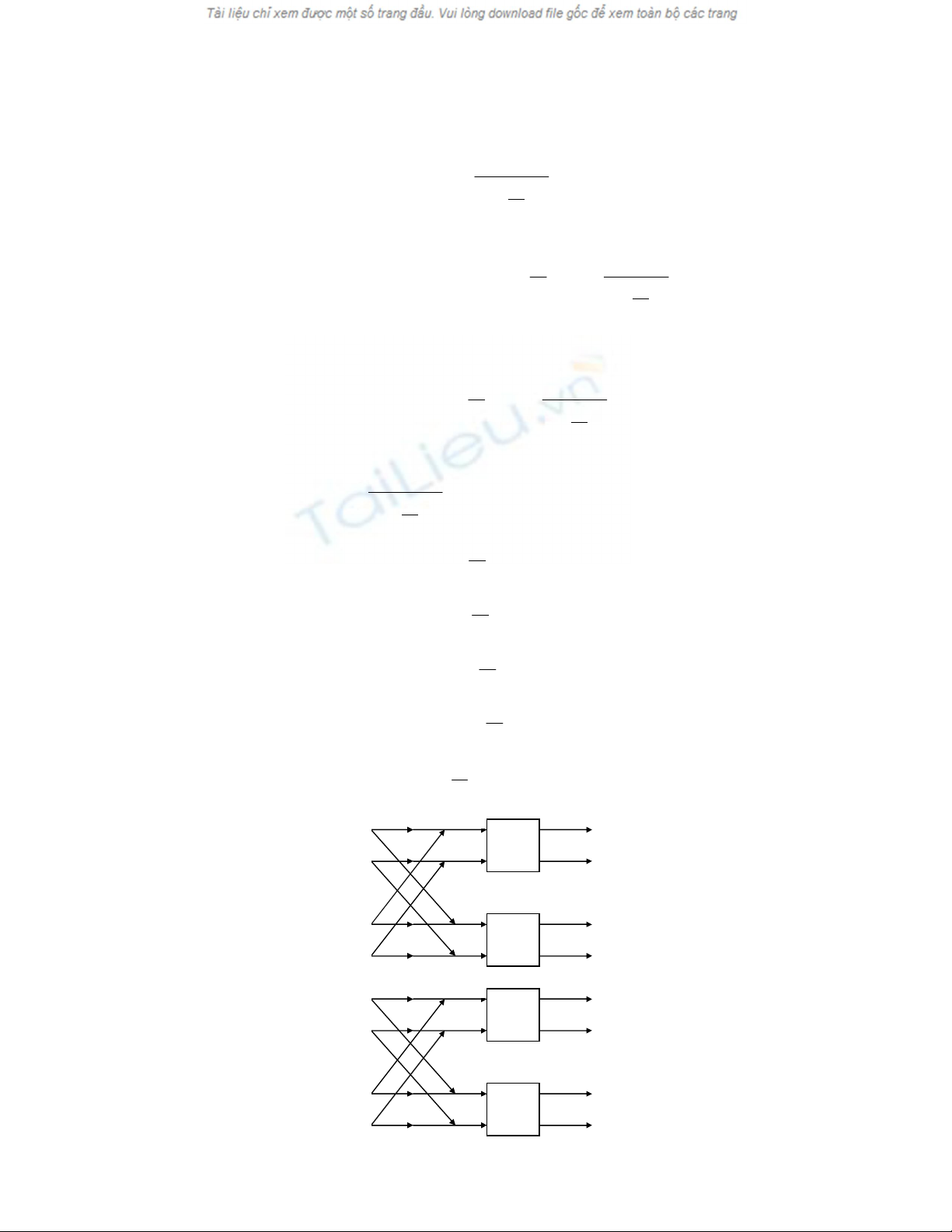
Hình 13.5 Bước thứ hai của thuật toán biến đổi cosin.
Biểu thức (13.22) đến (13.25) biểu diễn cho toán tử bướm. Thay các biểu
thức này vào các biểu thức từ (13.18) đến (13.21) chúng ta có:
14/
01000
4
2
)14(
cos)()2( N
nN
kn
nxkY
(13.27)
14/
0110000 )
4
(2
)14(
cos)()12()12( N
nN
kn
nxkYkY
(13.28)
14/
01201
4
2
)14(
cos)()2( N
nN
kn
nxkY
(13.29)
14/
0130101 )
4
(2
)14(
cos)()12()12( N
nN
kn
nxkYkY
(13.30)
Các biểu thức trên cho kết quả của bước thứ hai trên sơ đồ hình (13.5) trong
trường hợp N = 8.
Đặt )2()( 0010 kYkY (13.31)
)12()12()( 000011 kYkYkY (13.32)
Vì vậy
)2()( 0112 kYkY (13.33)
)12()12()( 010012 kYkYkY (13.34)
14/
01010 )
4
(2
)14(
cos)()( N
nN
kn
nxkY
(13.35)
14/
01111 )
4
(2
)14(
cos)()( N
nN
kn
nxkY
(13.36)
343
14/
01212 )
4
(2
)14(
cos)()( N
nN
kn
nxkY
(13.37)
14/
01212 )
4
(2
)14(
cos)()( N
nN
kn
nxkY
(13.38)
Nếu N = 8, các biểu thức trên có dạng:
4
5
cos)1(
4
cos)0()( 101010 k
x
k
xkY
(13.39)
4
5
cos)1(
4
cos)0()( 111111 k
x
k
xkY
(13.40)
4
5
cos)1(
4
cos)0()( 121212 k
x
k
xkY
(13.41)
4
5
cos)1(
4
cos)0()( 131313
k
x
k
xkY
(13.42)
ở đây k = 0,1.
Các biểu thức cuối có thể biểu diễn thành
Y10(0) = x10 (0) + x10(1)
Y10 = (x10(0) - x10(1))cos(/4)
...
v..v...
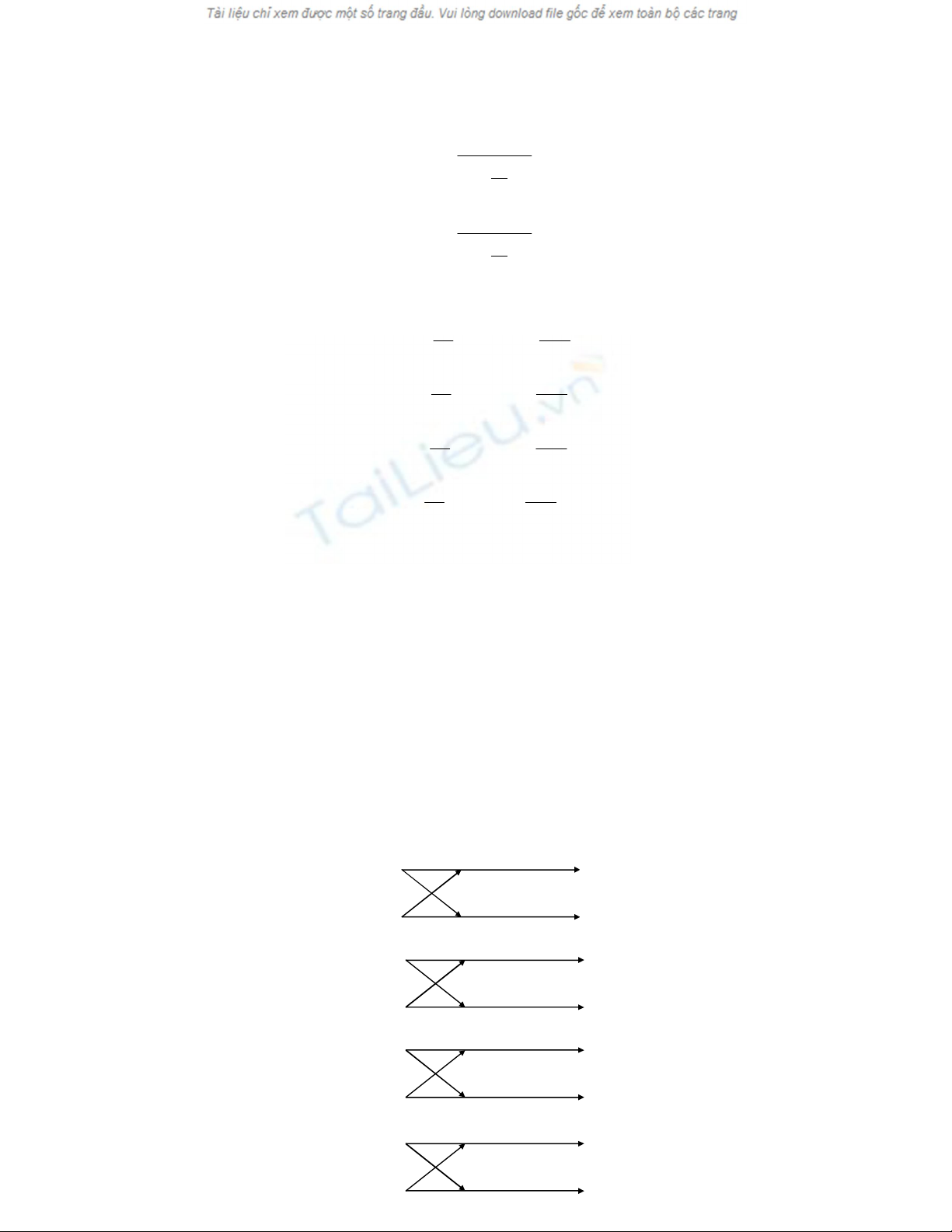
Các biểu thức này dẫn chúng ta đến lưu đồ bướm cuối cùng trình bày ở hình
13.6.
Để rút ra tín hiệu đầu ra của lưu đồ FCT chúng ta cần quay trở lại. Cho ví
dụ, từ biểu thức (13.21) và (13.15) chúng ta có thể viết:
X(4k) (k)Y10 (13.43)
x11(0)
x11(1)
Y
11(0)
Y
11(1)
1
C4
-
1
x12(0)
x12(1)
Y
12(0)
Y
12(1)
1
C4
-
1
x
14
(0)
Y
(0)
1
x13(0)
x13(1)
Y
13(0)
Y
13(1)
1
C4
-
1
x10(0)
x10(1)
Y
10(0)
Y
10(1)
1
C4
-
1


























