BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ CHÍNH THỨC
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2008 LẦN 2
Môn thi: TOÁN – Trung học phổ thông phân ban
HƯỚNG DẪN CHẤM THI
Bản Hướng dẫn chấm có 04 trang
I. Hướng dẫn chung
1. Nếu thí sinh làm bài không theo cách nêu trong đáp án mà vẫn đúng thì cho đủ
điểm từng phần như hướng dẫn quy định.
2. Việc chi tiết hoá thang điểm (nếu có) so với thang điểm trong Hướng dẫn chấm
phải đảm bảo không sai lệch với Hướng dẫn chấm và được thống nhất thực hiện
trong Hội đồng chấm thi.
3. Sau khi cộng điểm toàn bài, làm tròn đến 0,5 điểm (lẻ 0,25 làm tròn thành 0,5; lẻ
0,75 làm tròn thành 1,0 điểm).
II. Đáp án và thang điểm
CÂU
ĐÁP ÁN ĐIỂM
1. (2,5 điểm)
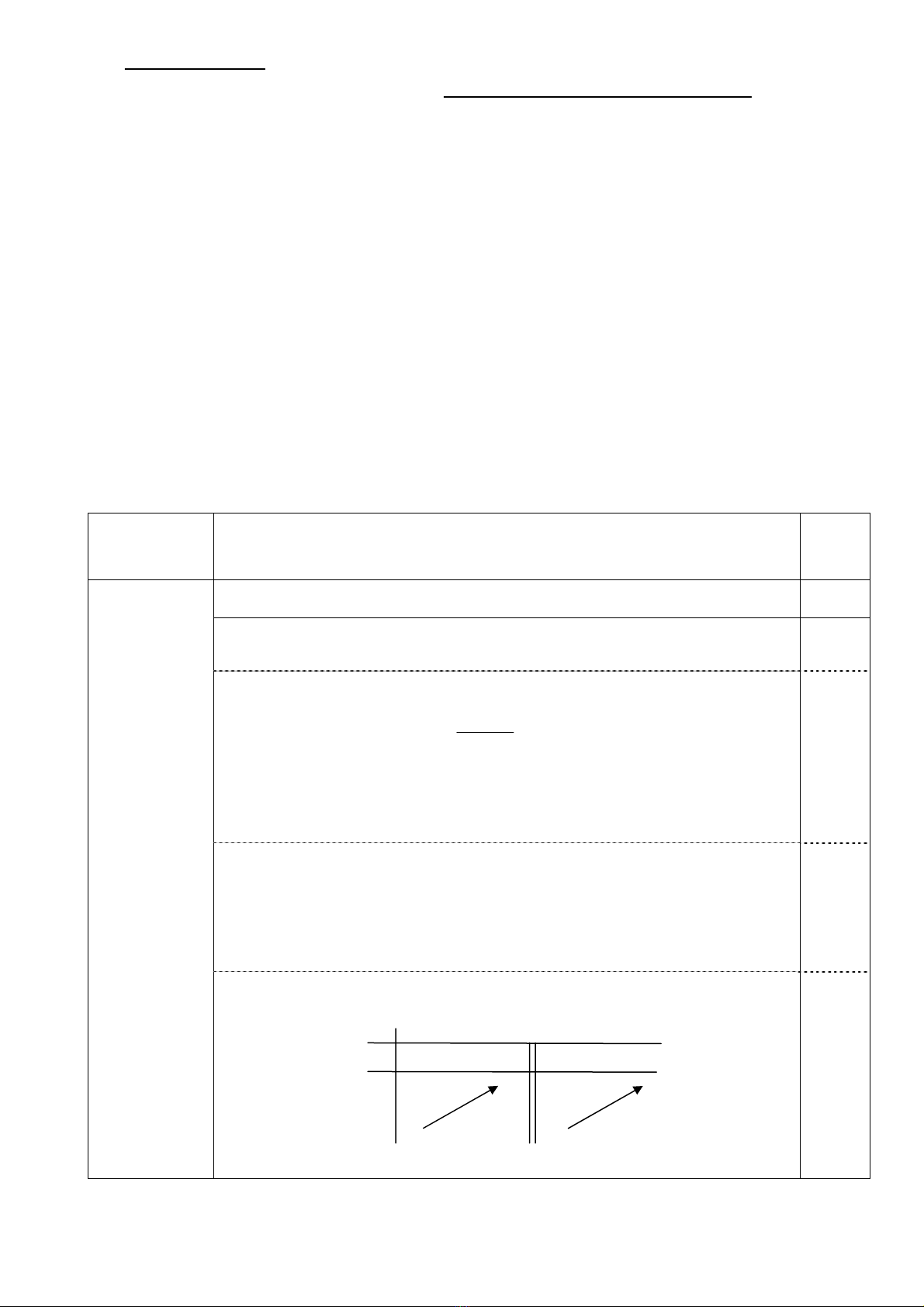
a) Tập xác định:
{
}
D\1=−\.
0,25
b) Sự biến thiên:
• Chiều biến thiên:
()
2
5
y' ,
x1
=
+
với ∀∈
y' 0>xD
1
.
Hàm số đồng biến trên các khoảng
()
và
()
;1−∞ − 1; .−+∞
• Cực trị: Hàm số không có cực trị.
0,75
• Giới hạn, tiệm cận:
Tiệm cận đứng: .
() ()
x1 x1
lim y , lim y .
−+
→− →−
=+∞ =−∞ x1=−
=
Tiệm cận ngang:
xx
lim y 3, lim y 3.
→−∞ →+∞
=y3.=
0,50
Câu 1
(3,5 điểm)
• Bảng biến thiên:
0,50
y
+∞
x −∞ 1−
y' + +
3
+∞
3
−∞
2
c) Đồ thị:
Đồ thị cắt trục Ox tại điểm 2;0 ,
3
⎛
⎜
⎝⎠
⎞
⎟
cắt trục Oy tại điểm
()
0; 2 .−
0,50
y
O
2. (1,0 điểm)
Điểm thuộc đồ thị có tung độ là điểm
()
y=−20; 2 ;−
()
y' 0 5.= 0,50
Phương trình tiếp tuyến cần tìm: hay
()
y5x0 2=−− y5x2.=− 0,50
Phương trình đã cho tương đương
()
2
33
x20
x20
log x 4 log 5
⎧+>
⎪
⎪−>
⎨
⎪−=
⎪
⎩
0,50
2
x2
x4
>
⎧
⇔⎨−=
⎩5
0,50
Câu 2
(1,5 điểm)
x2
x3.
x3
x3
>
⎧
⎪
⇔⇔
=
⎡
⎨⎢
⎪=−
⎣
⎩
=
Nghiệm của phương trình là
x3.=
0,50
()
2
2
44i 2i.Δ=− = = 0,50
Câu 3
(1,0 điểm)
Nghiệm của phương trình là: và x1i=+ x1i.=− 0,50
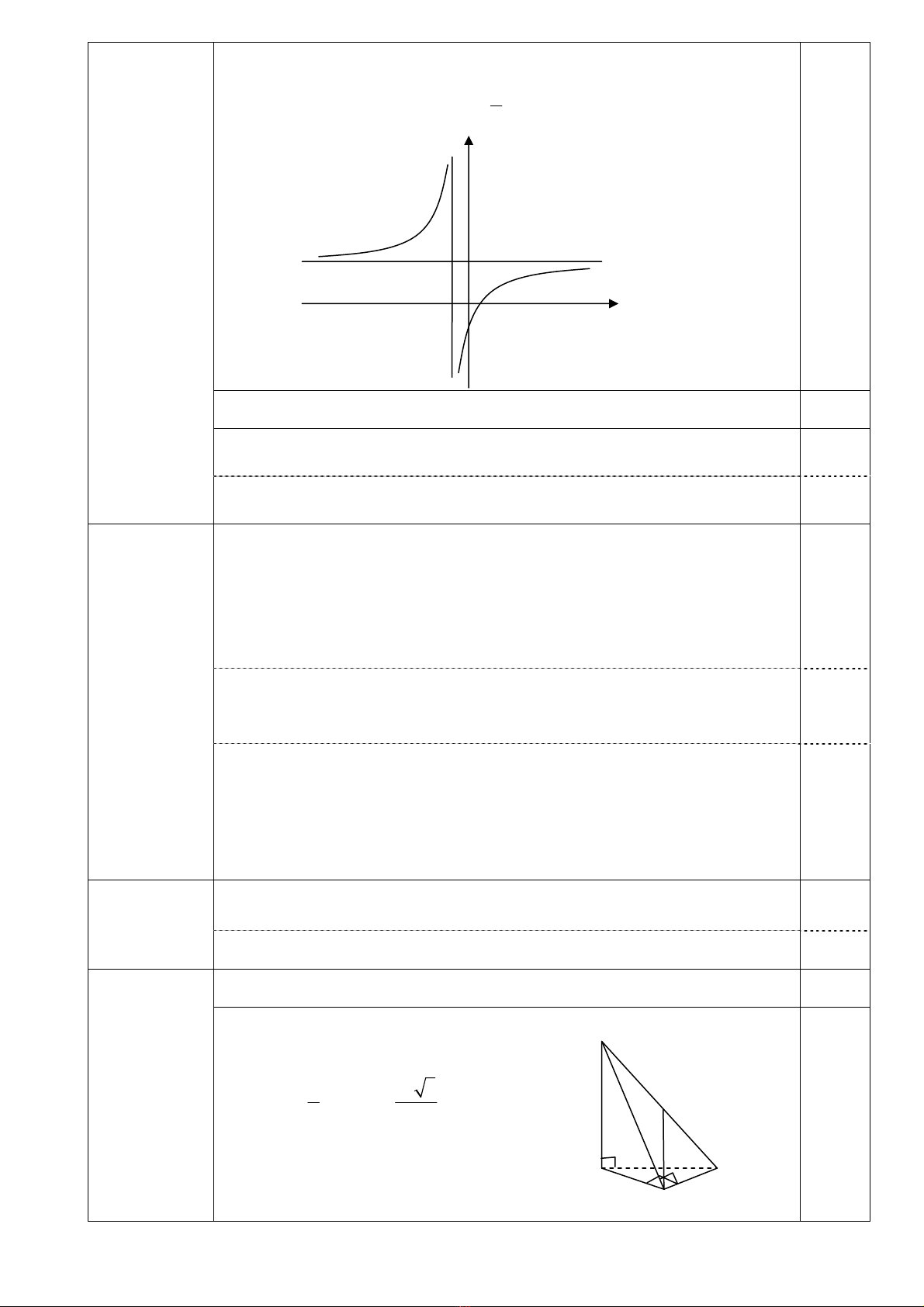
1. (1,0 điểm) Câu 4
(2,0 điểm) Tam giác ABC vuông tại B, nên
diện tích của tam giác ABC là:
2
ABC
1a
SBA.BC
22
Δ==
3
.
0,50
x
1−
3
2−
S
A
B
C
I
3
S.ABC ABC
1a
VSA.S
32
Δ
==
3
.0,50
Thể tích khối chóp S.ABC:
2. (1,0 điểm)
()
SA ABC⊥ và BC (định lý ba đường vuông góc).
Tam giác SBC vuông tại B, nên
AB⊥BC SB⇒⊥
0,50
SC
BI .
2
=
Tam giác SBC vuông tại B và tam giác SAB vuông tại A, nên:
Vậy 0,50
a13
BI .
2
=
222 2 2 2
SC SB BC SA AB BC 13a .=+ =+ + =
2
3
1. (1,0 điểm)
Câu 5a
Đặt u4 ta chọn
x1 du4dx;=+⇒=x
dv e dx,=x
ve.=
()
1
1
xx
00
I4x1e 4edx=+ −
∫
0,50
(2,0 điểm)
1
x
0
5e 1 4e e 3.=−− =+ 0,50
2. (1,0 điểm)
Trên đoạn
[
]
0; 2 , ta có:
() ()
3x0
f ' x 8x 8x; f ' x 0 x1.
=
⎡
=− + = ⇔⎢=
⎣0,50
Tính và hoặc lập bảng biến thiên của hàm
số, ta được: và
() ()
f0 3, f1 5==
()
f2 13=−
0,50
[]
() ()
0; 2
max f x f 1 5==
[]
() ()
0; 2
min f x f 2 13.==−
1. (1,0 điểm) Câu 5b
()
MN 4; 6; 2=−
J
JJJG
Vectơ chỉ phương đường thẳng MN: hay
(
u2;3;1=−
G
)
.
0,50
(2,0 điểm)
x1 y2 z
.
23
−+
==
−
Phương trình đường thẳng MN: 1
0,50
2. (1,0 điểm)
Trung điểm của đoạn thẳng MN:
()
I 1;1;1 .−0,50
()
2217
dI,(P) 2.
441
−+ +−
==
++
Khoảng cách từ I đến (P): 0,50
1. (1,0 điểm) Câu 6a
()
2
32
1
J2x2xx=−+
0,50
(2,0 điểm)
()()
16 8 2 2 2 1 9.=−+−−+= 0,50
2. (1,0 điểm)
Trên đoạn
[
]
1;1 ,− ta có:
() ()
2
f' x 6x 12x; f' x 0 x 0.=− =⇔= 0,50
Tính và hoặc lập bảng biến thiên của
hàm số, ta được: và
() ( )
f0 1, f 1 7=−=−
()
f1 3=−
0,50
[]
() ()
1; 1
max f x f 0 1
−==
[]
() ( )
1; 1
min f x f 1 7.
−=−=−
4
1. (1,0 điểm)
Câu 6b
Khoảng cách từ đến (P): A
()
()
22610
dA, P 144
+−−
=++ 0,50
(2,0 điểm)
12 4.
3
==
0,50
2. (1,0 điểm)
là một vectơ chỉ phương của đường thẳng cần tìm.
(
n1;2;2−−
G
)
0,50
Phương trình đường thẳng cần tìm:
x 2 t
y12
z 32t
=+
⎧
⎪=− −
⎨
⎪=−
⎩
t
.
0,50
……….Hết……….