BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHÍNH THỨC
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2011
Môn thi: TOÁN – Giáo dục trung học phổ thông
HƯỚNG DẪN CHẤM THI
(Văn bản gồm 04 trang)
I. Hướng dẫn chung
1) Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm
từng phần như hướng dẫn quy định.
2) Việc chi tiết hoá (nếu có) thang điểm trong hướng dẫn chấm phải đảm bảo không làm sai
lệch hướng dẫn chấm và phải được thống nhất thực hiện trong toàn Hội đồng chấm thi.
3) Sau khi cộng điểm toàn bài, làm tròn đến 0,5 điểm (lẻ 0,25 làm tròn thành 0,5; lẻ 0,75
làm tròn thành 1,0 điểm).
II. Đáp án và thang điểm
CÂU ĐÁP ÁN ĐIỂM
1. (2,0 điểm)
a) Tập xác định : 1
\2
D
⎧
⎫
=
⎨
⎬
⎩⎭
\. 0,25
b) Sự biến thiên :
• Chiều biến thiên :
()
2
4
'0,
21
yx
x
−
=<∀
−
D∈
.
Hàm số nghịch biến trên mỗi khoảng 1
;2
⎛⎞
−∞
⎜⎟
⎝⎠
và 1;
2
⎛⎞
⎜⎟
.
+∞
⎝⎠
0,50
• Tiệm cận :
1
2
lim
x
y
−
⎛⎞
→⎜⎟
⎝⎠
=−∞ ;
1
2
lim
x
y
+
⎛⎞
→⎜⎟
⎝⎠
=+∞ 1
2
x⇒= là tiệm cận đứng.
lim 1
x
y
→−∞
=;lim 1
x
y
→+∞
=1y⇒= là tiệm cận ngang.
0,50
Câu 1
(3,0 điểm)
• Bảng biến thiên :
1
x
−∞ 1
2+∞
− −
'y
y
−∞
+∞
1
1
0,25
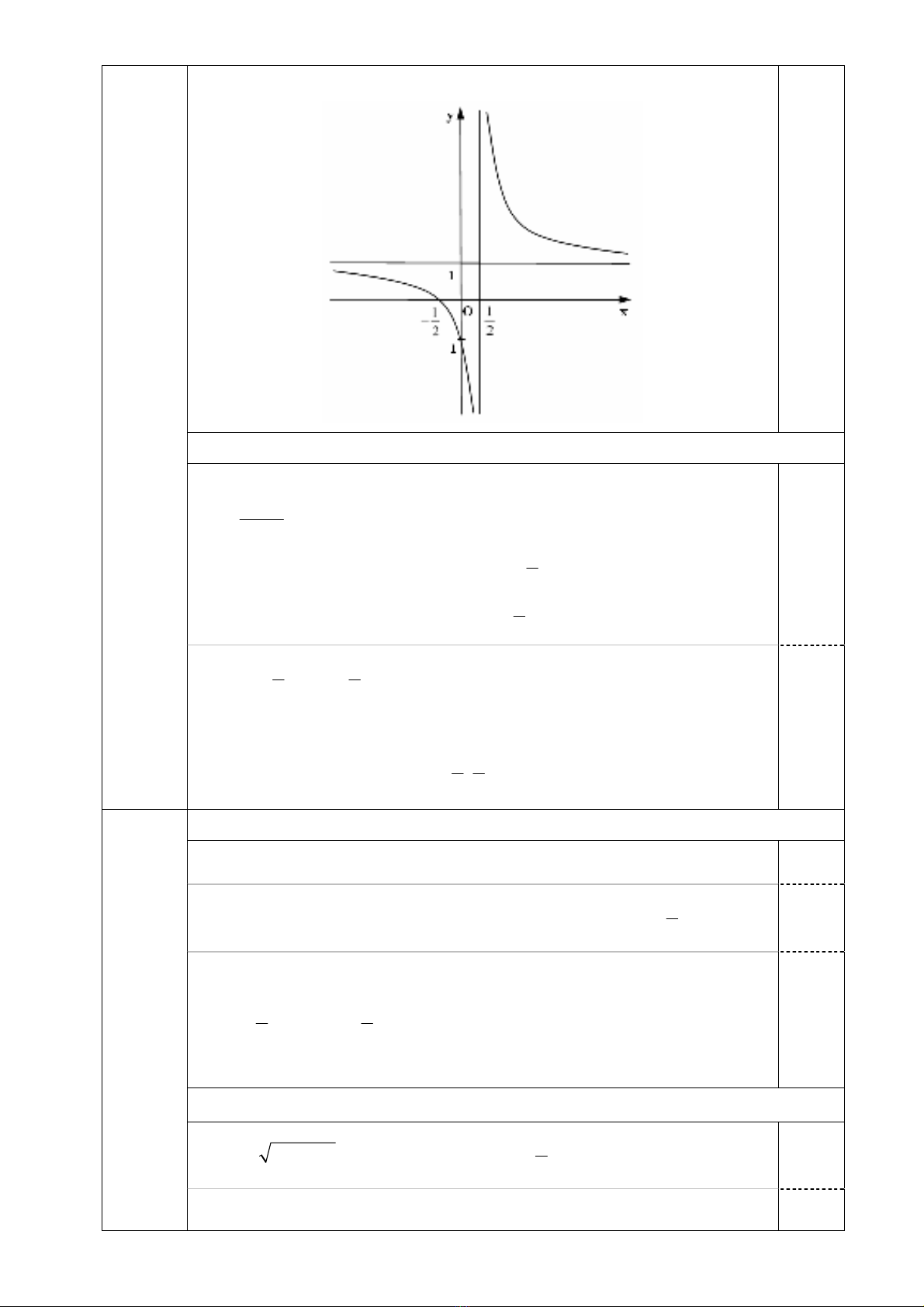
c) Đồ thị (C):
0,50
2. (1,0 điểm)
Hoành độ giao điểm của với đường thẳng là nghiệm của phương
trình
()C2yx=+
21 2
21
x
x
x
+=+
− (1)
(1) ⇔+ (2 (vì
21(21)(2xxx
2
)= − + )1
2
x= không là nghiệm của (2))
2
230=1
xx⇔+−
x
⇔= hoặc 3
2
x=− .
0,50
Với 3
2
x=− thì 1
2
y=.
Với 1
x
= thì . 3y=
Vậy tọa độ giao điểm cần tìm là 31
;
22
⎛⎞
−
⎜⎟
⎝⎠
và ( . 1;3)
0,50
1. (1,0 điểm)
Đặt 7
x
t(t). =>00,25
Phương trình đã cho trở thành 78 hoặc
210 1tt t−+=⇔= 1
7
t=. 0,25
Với t, ta có 7 . 1=1 0
xx=⇔ =
Với 1
7
t, ta có =1
71.
7
xx=⇔=−
Vậy nghiệm của phương trình là hoặc .
0x=1x=−
0,50
2. (1,0 điểm)
Đặt 25
45ln 45ln 2
txtxtdtdx
x
=+ ⇒=+ ⇒=. 0,25
Câu 2
(3,0 điểm)
Đổi cận : 12
t=⇒= và 3
x
et=⇒=. 0,25
Do đó
33
23 33
2
2
222
32
51515
Itdtt ⎛⎞
===−=
⎜⎟
⎝⎠
∫38
15
. 0,50
3. (1,0 điểm)
Ta có 2
'3 4
y
xx=−+m. 0,25
Nếu hàm số đạt cực tiểu tại 1
x
= thì , suy ra . '(1) 0y=1m=0,25
Với thì 1m=32
21
y
xxx=− ++, 2
'3 4 1
y
xx=−+ và " 6 4
y
x=−.
Mà và nên hàm số đạt cực tiểu tại '(1) 0y=
()
"1 2 0y=> 1
x
=. 0,25
Vậy là giá trị cần tìm. 1m=0,25
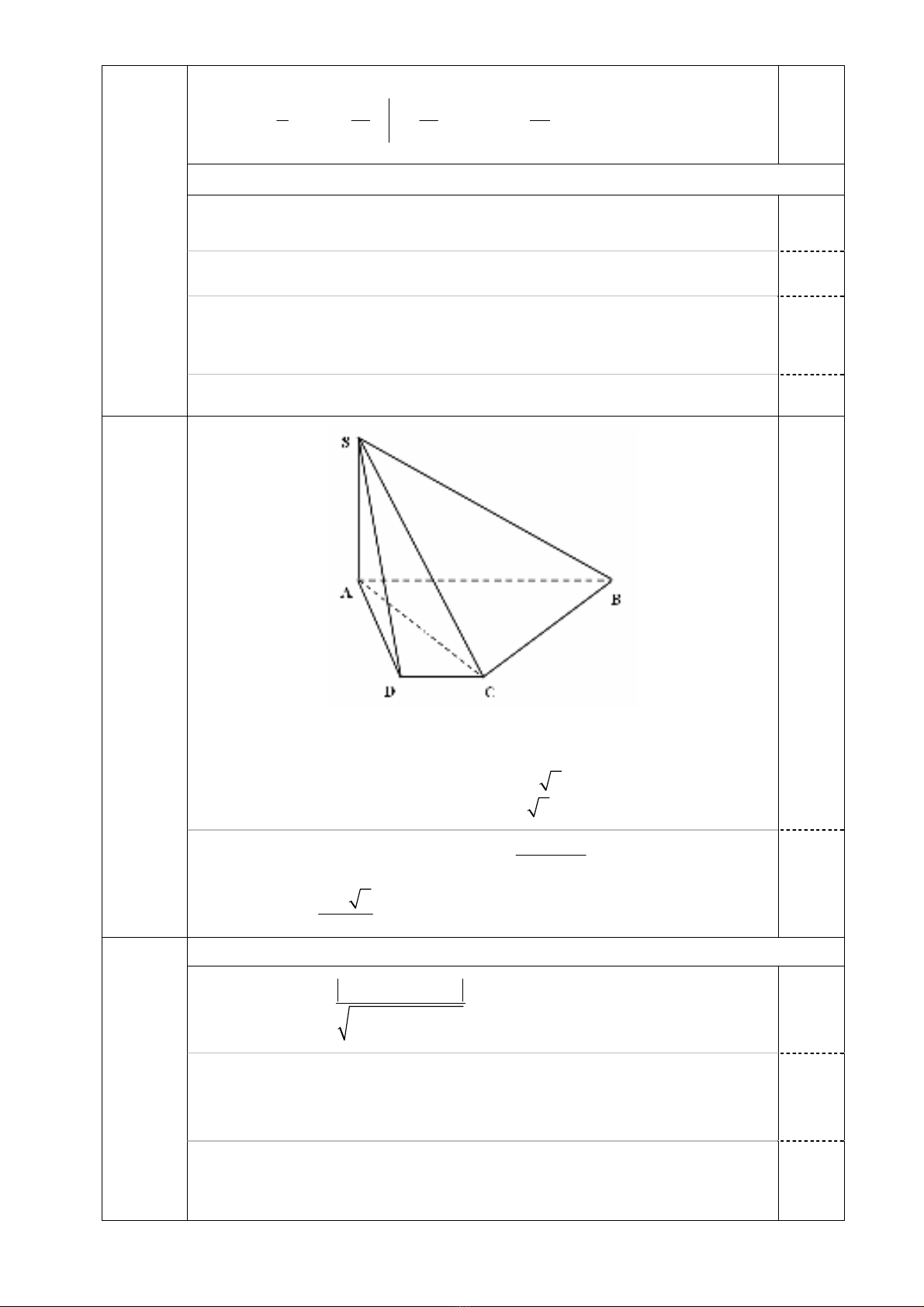
Ta có nên là hình chiếu của trên ()SA ABCD⊥AC SC ()
A
BCD .
Do đó .
n
45o
SCA =
Tam giác vuông cân tại nên ACD D2AC a=.
Tam giác vuông cân tại SAC
A
nên 2SA a=.
0,50
Câu 3
(1,0 điểm)
Diện tích của hình thang vuông
A
BCD là 2
(3) 2
2
aaa a
+=.
Vậy
3
.
22
3
SABCD
a
V=.
0,50
1. (1,0 điểm)
Ta có
()
22 2
2.3 2.1 1.0 1
,( ) 3
22(1)
dAP +−+
==
++−
. 0,50
Ta có là vectơ pháp tuyến của .
(2;2; 1)n=−
G()P
()Qsong song với ( nên ( nhận )P)Q(2;2; 1)n=−
G
làm vectơ pháp tuyến. 0,25
Câu 4.a
(2,0 điểm)
Mặt khác ( qua nên có phương trình )Q(3;1;0)A( )Q
2( 3) 2( 1) 1( 0) 0 2 2 8 0xyz xyz−+ −− −=⇔ + −−=. 0,25
3
2. (1,0 điểm)
Gọi là đường thẳng qua và vuông góc với thì
dA( )P(2;2; 1)n=−
G
là
vectơ chỉ phương của .
d
Do đó phương trình tham số của là d
32
12
x
t
y
t
zt
=+
⎧
⎪=+
⎨
⎪=−
⎩
.
0,50
Gọi là hình chiếu của
H
A
trên ( thì là giao điểm của và (.
)P H d)P
Do nên . Hd∈(3 2 ;1 2 ; )Htt++−t
Mặt khác nên ta có .
()HP∈2(3 2 ) 2(1 2 ) ( ) 1 0ttt+++−−+= 1t⇔=−
Vậy .
(1; 1;1)H−
0,50
Phương trình đã cho tương đương với phương trình ( 1 ) 2 4iz i−=− 0,25
24 (24)(1 )
1(1)(1
ii
zz
ii
−−
⇔= ⇔=
−−
)
i
i
+
+
0,25
Câu 5.a
(1,0 điểm)
(2 4 )(1 )
2
ii
z−+
⇔= 62 3
2
i
zz
−
⇔= ⇔=−
i.
Vậy nghiệm của phương trình là .
3zi=−
0,50
1. (1,0 điểm)
Ta có (1;2;2); (1;0;1)AB AC=− − − =− −
JJJG JJJG , (2;1; 2)AB AC
⎡⎤
⇒=−
⎣⎦
J
JJG JJJG . 0,50
Mặt phẳng qua , nhận ( )ABC A,AB AC
⎡
⎤
⎣
⎦
J
JJGJJJG làm vectơ pháp tuyến nên có
phương trình .
2(x 0) 1(y 0) 2(z 3) 0−+ −− −= 2x y 2z 6 0⇔+−+= 0,50
2. (1,0 điểm)
Ta có:
A
BC
SΔ 1,
2AB AC
⎡⎤
=⎣⎦
JJJG JJJG 22 2
13
21(2)
22
=++−=
. 0,50
Câu 4.b
(2,0 điểm)
222
( 1 1) (0 2) (2 1) 5BC =−+ ++ +− = .
Gọi
A
H là đường cao của tam giác thì ABC 23
5
ABC
S
AH BC
Δ
==.
0,50
Phương trình đã cho tương đương với phương trình
2230ziz−+=.
Ta có .
()
22
412164iiΔ= − =− =
0,50
Câu 5.b
(1,0 điểm)
Vậy phương trình có hai nghiệm là 1
24 3
2
ii
zi
+
==
và 2
24
2
ii
zi
−
==
−. 0,50
--------------- Hết ---------------
4