1
bé gi¸o dôc vμ ®μo t¹o
®Ò thi chÝnh thøc
kú thi tèt nghiÖp trung häc phæ th«ng n¨m 2008
M«n thi: to¸n – Bæ tóc trung häc phæ th«ng
H−íng dÉn chÊm thi
B¶n h−íng dÉn chÊm gåm 03 trang
I. H−íng dÉn chung
1) NÕu thÝ sinh lµm bµi kh«ng theo c¸ch nªu trong ®¸p ¸n mµ vÉn
®óng th× cho ®ñ ®iÓm tõng phÇn nh− h−íng dÉn quy ®Þnh.
2) ViÖc chi tiÕt ho¸ thang ®iÓm (nÕu cã) so víi thang ®iÓm trong
h−íng dÉn chÊm ph¶i ®¶m b¶o kh«ng sai lÖch víi h−íng dÉn chÊm
vµ ®−îc thèng nhÊt thùc hiÖn trong Héi ®ång chÊm thi.
3) Sau khi céng ®iÓm toµn bµi, lµm trßn ®Õn 0,5 ®iÓm (lÎ 0,25 lµm trßn
thµnh 0,5; lÎ 0,75 lµm trßn thµnh 1,0 ®iÓm).
II. §¸p ¸n vµ thang ®iÓm
c©u §¸p ¸n §iÓm
1. (2,5 ®iÓm)
a) TËp x¸c ®Þnh: R
0,25
b) Sù biÕn thiªn:
• ChiÒu biÕn thiªn: 2
y
=3x - 6x =3x(x -2).
′ Ph−¬ng tr×nh 0y =
′ cã nghiÖm:
x = 0, x = 2.
()()
∞+∪∞−∈⇔>
′;20;x0y ,
()
2;0x0y ∈⇔<
′.
Hµm sè ®ång biÕn trªn c¸c kho¶ng
()
0;∞− vµ
()
∞+;2 , nghÞch biÕn trªn
kho¶ng (0; 2).
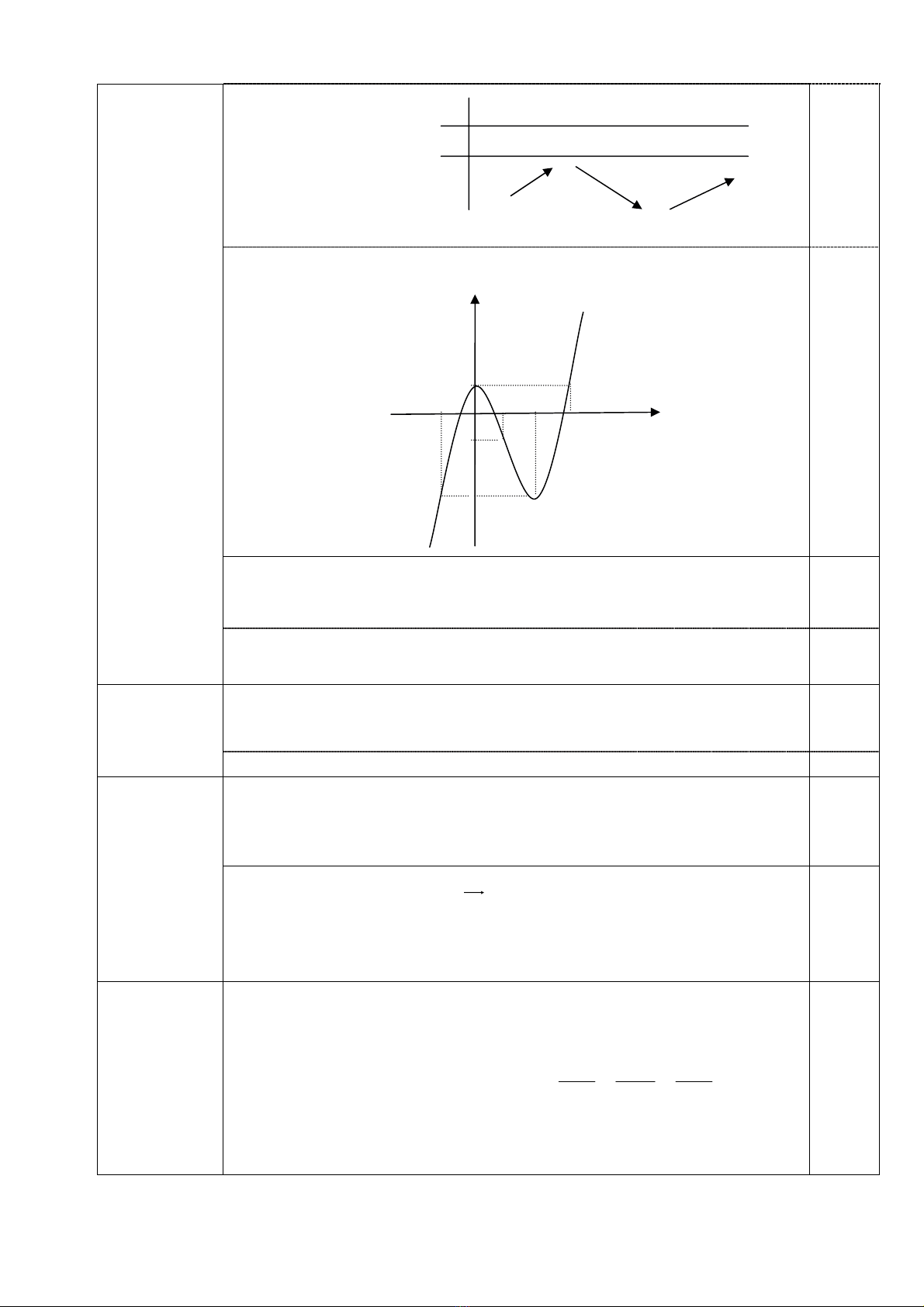
Hµm sè ®¹t cùc ®¹i t¹i x = 0, yC§ = 1, ®¹t cùc tiÓu t¹i x = 2, yCT = -3.
0,75
C©u 1
(3,5 ®iÓm)
• −∞=
−∞→ylim
x,∞+=
+∞→ylim
x
•TÝnh låi lâm vµ ®iÓm uèn cña ®å thÞ:
y’’ = 6x - 6, y’’ 01.x=⇔=
y’’> 0 khi x > 1, y’’< 0 khi x < 1.
VËy ®å thÞ hµm sè lâm trªn kho¶ng );1( ∞+ , låi trªn kho¶ng )1;(−∞ vµ cã
mét ®iÓm uèn U(1; - 1).
0,50
2
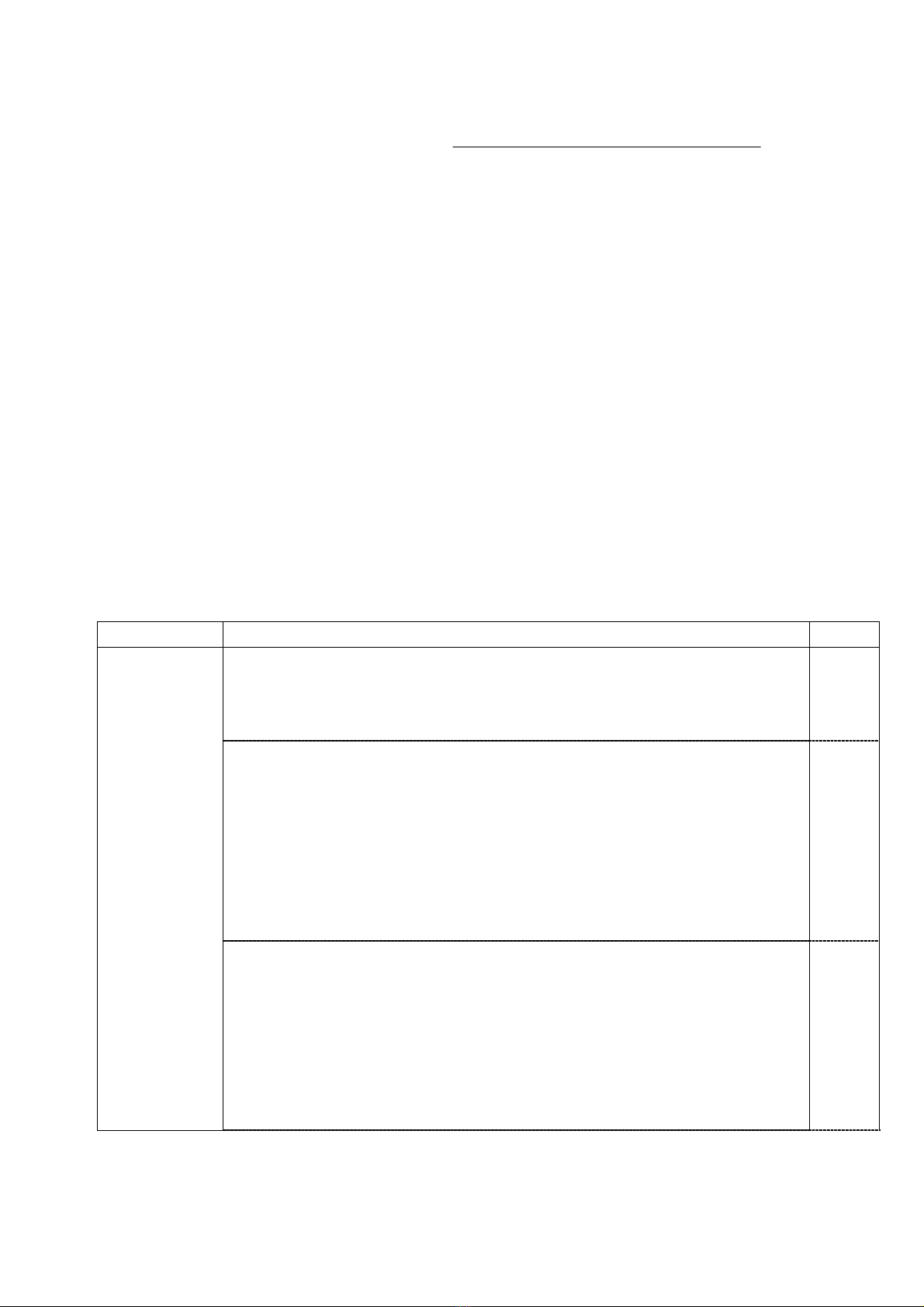
• B¶ng biÕn thiªn:
0,50
c) §å thÞ: Giao ®iÓm cña ®å thÞ víi trôc tung (0; 1).
0,50
2. (1,0 ®iÓm)
Khi x = 3 th× y =1; (3)
y=9.
′
0,50
Ph−¬ng tr×nh tiÕp tuyÕn cÇn t×m lµ:
y -1 = )3(
y′(x -3) hay y = 9x – 26. 0,50
y = - 2sin(2x -1),
′y=-4cos(2x-1).
′′
0,50
C©u 2
(1,0 ®iÓm)
y + 4y = -4cos(2x -1) + 4cos(2x -1) = 0.
′′ 0,50
1. (0,75 ®iÓm)
x2 + y2 – 2x – 15 = 0 ⇔(x - 1)2 + y2 = 16.
§−êng trßn ®· cho cã t©m I(1; 0), b¸n kÝnh R = 4.
0,75
C©u 3
(1,5 ®iÓm)
2. (0,75 ®iÓm)
TiÕp tuyÕn cÇn t×m nhËn vect¬ )4;0(IA =lµ mét vect¬ ph¸p tuyÕn.
Ph−¬ng tr×nh tiÕp tuyÕn lµ:
0(x -1) + 4(y - 4) = 0 ⇔y – 4 = 0.
0,75
C©u 4
(2,0 ®iÓm)
1. (0,75 ®iÓm)
§−êng th¼ng cÇn t×m vu«ng gãc víi mÆt ph¼ng(),α nhËn vect¬
n(1; 2;2)=−
G
lµ mét vect¬ chØ ph−¬ng.
Ph−¬ng tr×nh chÝnh t¾c cña ®−êng th¼ng lµ: 2
3z
2
2y
1
1x −
=
−
−
=
+. 0,75
x
y
O
-1
2
1
1
-
3
∞−
0
02
0
+∞
∞−
+∞
x
y
’
y
1
-
3
-++
1
-1
3
2. (1,25 ®iÓm)
MÆt ph¼ng )(
β
song song víi mÆt ph¼ng )(α nªn )(
β
nhËn n lµ mét vect¬
ph¸p tuyÕn.
Ph−¬ng tr×nh )(
β
lµ:
1(x + 1) - 2(y – 2) + 2(z - 3) = 0 ⇔x – 2y + 2z – 1 = 0.
0,75
Kho¶ng c¸ch gi÷a hai mÆt ph¼ng )(α vµ )(
β
lµ:
2
3
6
2)2(1
53.22.2)1.(1
))(,M(dd 222 ==
+−+
++−−
=α= .
0,50
1. (1,0 ®iÓm)
I cos x sin xdx sin xd(sin x)
ππ
==
∫∫
44
00
0,50
π
22
4
0
1121
I= sin x = [( ) -0]= .
2224
0,50
2. (1,0 ®iÓm)
§K: nN,n2.∈≥
Ph−¬ng tr×nh ®· cho cã d¹ng: 07
)!1n(
)!1n(
)!2n(!2
!n
3=−
−
+
−
−
0,50
C©u 5
(2,0 ®iÓm)
014n5n 2=−−⇔
⇔ ⎢
⎣
⎡
−=
=
2n
7n . NghiÖm tho¶ m·n ®iÒu kiÖn lµ n = 7.
Ph−¬ng tr×nh cã nghiÖm n =7.
0,50
……….HÕt……….