1
bé gi¸o dôc vµ ®µo t¹o
®Ò thi chÝnh thøc
kú thi tèt nghiÖp trung häc phæ th«ng n¨m 2007
M«n thi: to¸n – Trung häc phæ th«ng kh«ng ph©n ban
H−íng dÉn chÊm thi
B¶n h−íng dÉn chÊm gåm 03 trang
I. H−íng dÉn chung
1) NÕu thÝ sinh lµm bµi kh«ng theo c¸ch nªu trong ®¸p ¸n mµ vÉn ®óng th× cho
®ñ ®iÓm tõng phÇn nh− h−íng dÉn quy ®Þnh.
2) ViÖc chi tiÕt ho¸ thang ®iÓm (nÕu cã) so víi thang ®iÓm trong h−íng dÉn
chÊm ph¶i ®¶m b¶o kh«ng sai lÖch víi h−íng dÉn chÊm vµ ®−îc thèng nhÊt
thùc hiÖn trong Héi ®ång chÊm thi.
3) Sau khi céng ®iÓm toµn bµi, lµm trßn ®Õn 0,5 ®iÓm (lÎ 0,25 lµm trßn thµnh
0,5; lÎ 0,75 lµm trßn thµnh 1,0 ®iÓm).
II. §¸p ¸n vµ thang ®iÓm
c©u §¸p ¸n §iÓm
1. (2,5 ®iÓm)
a) TËp x¸c ®Þnh: D = R\ .
2
1
⎭
⎬
⎫
⎩
⎨
⎧ 0,25
b) Sù biÕn thiªn:
• ChiÒu biÕn thiªn: y’ = 1 + 2
)12(
4
−x
; y’ > 0 víi mäi x ∈ D.
- Hµm sè ®ång biÕn trªn c¸c kho¶ng ⎟
⎠
⎞
⎜
⎝
⎛∞− 2
1
; vµ .;
2
1⎟
⎠
⎞
⎜
⎝
⎛∞+
• Cùc trÞ: Hµm sè kh«ng cã cùc trÞ.
0,75
C©u 1
(3,5 ®iÓm)
• Giíi h¹n vµ tiÖm cËn: −∞=
−∞→
y
x
lim ; +∞=
+∞→
y
x
lim
+∞=
−
→
y
x2
1
lim vµ −∞=
+
→
y
x2
1
lim ⇒ tiÖm cËn ®øng: .
2
1
=x
[]
0)1(lim =+−
∞→
xy
x
⇒ tiÖm cËn xiªn: .1+= xy
0,50
2
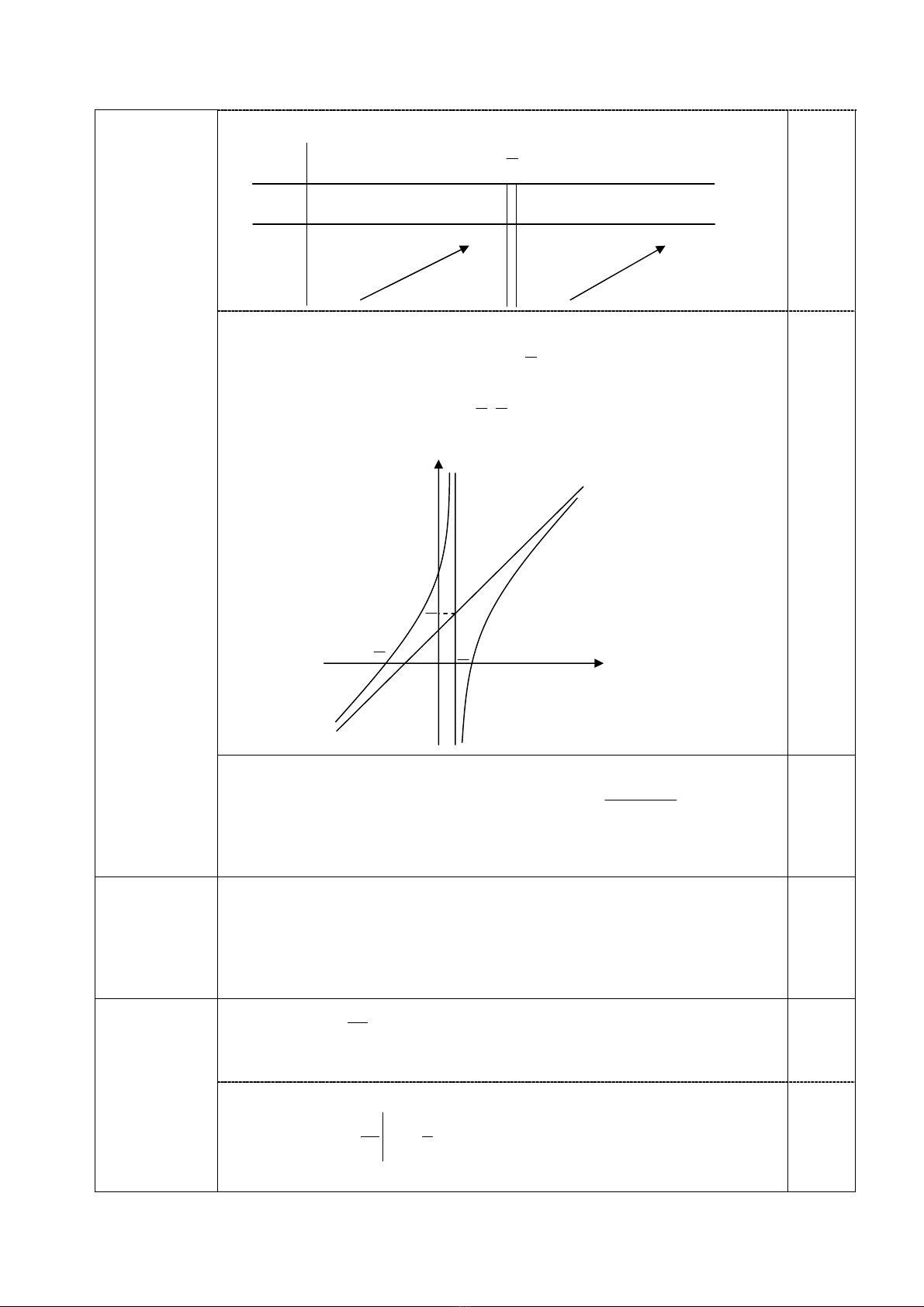
• B¶ng biÕn thiªn:
0,50
c) §å thÞ:
- §å thÞ c¾t Ox t¹i c¸c ®iÓm: (1; 0) vµ ⎟
⎠
⎞
⎜
⎝
⎛−0;
2
3; c¾t Oy t¹i ®iÓm (0; 3).
- §å thÞ hµm sè nhËn giao ®iÓm I⎟
⎠
⎞
⎜
⎝
⎛
2
3
;
2
1 cña hai ®−êng tiÖm cËn lµm t©m
®èi xøng.
0,50
2.(1,0 ®iÓm)
- HÖ sè gãc cña tiÕp tuyÕn t¹i A(0; 3) lµ: y’(0) = 1 + 2
)10.2(
4
−
= 5.
- VËy ph−¬ng tr×nh tiÕp tuyÕn víi ®å thÞ (H) t¹i ®iÓm A(0; 3) lµ:
3)0).(0(' +−= xyy hay 35 += xy .
1,00
C©u 2
(1,0 ®iÓm)
- Ta cã .729)(' 2−−= xxxf
- XÐt trªn ®o¹n
[]
2;0 ta cã 0)(' =xf ⇔x = 1.
MÆt kh¸c f(0) = 1; f(1) =4−; f(2) = 7.
VËy
[]
.7)2()(max
2;0
== fxf
1,00
- §Æt lnx = t ⇒ .dt
x
dx =
- Víi x = 1 th× t = 0, víi x = eth× t = 1.
0,50
C©u 3
(1,0 ®iÓm)
VËy dttJ ∫
=
1
0
2 = 0
1
3
3
t = .
3
1
0,50
x ∞− 2
1 ∞+
y’ + +
∞+ ∞+
y
∞− ∞−
3
y
x
2
3
− -1 O2
1
1
2
3 I
3
- Ph−¬ng tr×nh chÝnh t¾c cña (E) cã d¹ng: ).0(1
2
2
2
2
>>=+ ba
b
y
a
x
- Theo ®Ò ra ta cã: a = 5, b = 4 ⇒ c = 22 ba −= 3.
- To¹ ®é c¸c tiªu ®iÓm: )0;3(
1−F, ).0;3(
2
F
0,75
C©u 4
(1,5 ®iÓm)
- §é dµi trôc lín: 2a = 10.
- §é dµi trôc bÐ: 2b = 8.
- T©m sai: e = 5
3
=
a
c.
0,75
1. (1,0 ®iÓm)
- Ph−¬ng tr×nh tham sè cña ®−êng th¼ng (d) lµ: ⎪
⎩
⎪
⎨
⎧
+=
+−=
+=
.31
21
2
tz
ty
tx
- To¹ ®é giao ®iÓm M(x; y; z) tho¶ m·n hÖ:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=++−
+=
+−=
+=
.023
31
21
2
zyx
tz
ty
tx
0,50
- Gi¶i hÖ ta ®−îc:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−=
−=
=
−=
.2
3
1
1
z
y
x
t
VËy M(1; -3; -2).
0,50
C©u 5
(2,0 ®iÓm)
2. (1,0 ®iÓm)
- Gäi (Q) lµ mÆt ph¼ng chøa (d) vµ vu«ng gãc víi (P).
- §−êng th¼ng (d) cã mét vÐc t¬ chØ ph−¬ng lµ ).3;2;1(=u
- MÆt ph¼ng (P) cã mét vect¬ ph¸p tuyÕn lµ ).3;1;1( −=n
- Vect¬ ph¸p tuyÕn cña (Q) lµ: [ nu,]).3;0;9( −=
VËy ph−¬ng tr×nh cña mÆt ph¼ng (Q) lµ:
3(x – 2) + 0(y +1) – 1(z -1) = 0 ⇔ 3x – z – 5 = 0.
1,00
- §iÒu kiÖn: n ∈N, n 5≥.
- Ph−¬ng tr×nh ®· cho t−¬ng ®−¬ng víi: !!(1)!
3.
4!( 4)! 5!( 5)! 6!( 5)!
nn n
nn n
+
+=
−− −
0,50
C©u 6
(1,0 ®iÓm)
⇔10
1
5
1
4
1+
=+
−
n
n ⇔10
1
)4(5
1+
=
−
+n
n
n
⇔n = 6.
0,50
……….HÕt……….