1
Bé gi¸o dôc vµ ®µo t¹o
§Ò thi chÝnh thøc
kú thi tèt nghiÖp trung häc phæ th«ng n¨m 2006
M«n thi: To¸n - Bæ tóc trung häc phæ th«ng
h−íng dÉn chÊm THi
B¶n h−íng dÉn chÊm gåm 03 trang
I. H−íng dÉn chung
1. NÕu thÝ sinh lµm bµi kh«ng theo c¸ch nªu trong ®¸p ¸n mµ vÉn ®óng th× cho ®ñ
®iÓm tõng phÇn nh− h−íng dÉn quy ®Þnh.
2. ViÖc chi tiÕt ho¸ thang ®iÓm (nÕu cã) so víi thang ®iÓm trong h−íng dÉn chÊm ph¶i
®¶m b¶o kh«ng sai lÖch víi h−íng dÉn chÊm vµ ®−îc thèng nhÊt thùc hiÖn trong Héi
®ång chÊm thi.
3. Sau khi céng ®iÓm toµn bµi míi lµm trßn ®iÓm thi theo nguyªn t¾c: §iÓm toµn bµi
®−îc lµm trßn ®Õn 0,5 ®iÓm (lÎ 0,25 lµm trßn thµnh 0,5; lÎ 0,75 lµm trßn thµnh 1,0
®iÓm).
II. §¸p ¸n vµ thang ®iÓm
§¸p ¸n §iÓm
C©u 1
(3,5 ®iÓm)
1. (2,5 ®iÓm)
a) TËp x¸c ®Þnh: R.
b) Sù biÕn thiªn:
• ChiÒu biÕn thiªn: 2
y' 3x 6x ; y' 0=+ =⇔ x = 0 hoÆc x = −2.
y' > 0 x2⇔<− hoÆc x > 0; y' < 0 ⇔ 2x0.−< <
Hµm sè ®ång biÕn trªn c¸c kho¶ng ( −∞; −2) vµ (0; +∞), hµm sè nghÞch
biÕn trªn kho¶ng (−2; 0).
• Cùc trÞ: Hµm sè ®¹t cùc ®¹i t¹i x = −2 ; yC§ = y( −2) = 4.
Hµm sè ®¹t cùc tiÓu t¹i x = 0 ; yCT = y(0) = 0.
• Giíi h¹n: xx
lim y ; lim y
→− ∞ →+ ∞
=−∞ =+∞.
• TÝnh låi, lâm vµ ®iÓm uèn: y'' 6x 6 ; y'' 0=+ =
⇔ x1=− .
x −∞ −1 +∞
y'' − 0 +
§å thÞ låi §iÓm uèn lâm
U( −1; 2)
• B¶ng biÕn thiªn:
x −∞ −2 −1 0 +∞
y' + 0 − 0 +
y 4 +∞
−∞ 0
0,25
0,25
0,25
0,25
0,25
0,25
0,50
2
2
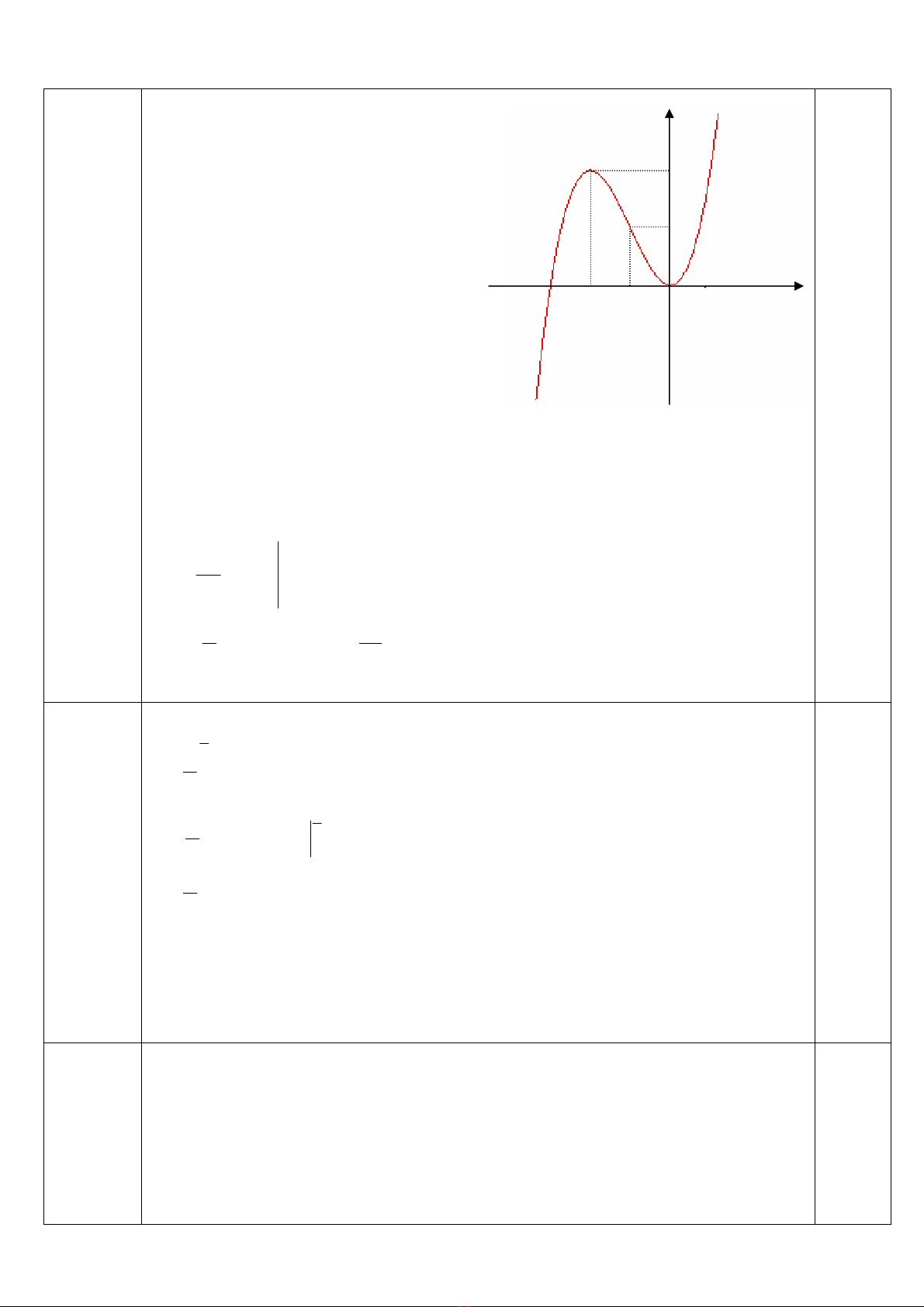
c) §å thÞ:
Giao ®iÓm cña ®å thÞ víi c¸c
trôc täa ®é: ( −3; 0), (0; 0).
§å thÞ nh− h×nh bªn.
§å thÞ nhËn ®iÓm U( −1; 2)
lµm t©m ®èi xøng.
2. (1,0 ®iÓm)
V× 32
x3x0+≥ x[2;1]∀∈− − nªn diÖn tÝch h×nh ph¼ng cÇn t×m :
()
132
2
S x 3x dx
−
−
=+
∫
1
43
2
xx
4
−
−
⎛⎞
=+
⎜⎟
⎝⎠
=
()
1148
4
⎛⎞
−− −
⎜⎟
⎝⎠ = 13
4 (®vdt).
0,50
0,50
0,25
0,25
C©u 2
(1,5 ®iÓm)
1. (1,0 ®iÓm)
2
0
1
J(2sinx3)d(2sinx3)
2
π
=++
∫
2
2
0
1(2sin x 3)
4
π
=+
()()
22
123 03
4
⎡⎤
=+−+
⎣⎦
= 4.
2. (0,5 ®iÓm)
y' = x2 − 2mx − 2m − 3.
∆' = (m + 1)2 + 2 > 0, ∀m .
Do vËy hµm sè lu«n cã cùc trÞ víi mäi gi¸ trÞ cña tham sè m .
0,50
0,25
0,25
0,25
0,25
C©u 3
(2,0 ®iÓm)
1. (1,0 ®iÓm)
T©m cña ®−êng trßn (T): I(1; 3).
VÐc t¬ chØ ph−¬ng cña (∆): u
G
= (2; 1).
V× (∆') ⊥ (∆) nªn u
G
= (2; 1) lµ mét vÐct¬ ph¸p tuyÕn cña (∆').
Ph−¬ng tr×nh (∆'): 2(x − 1) + 1(y − 3) = 0 ⇔ 2x + y − 5 = 0.
0,25
0,25
0,25
0,25
y
-3 -2 -1 O 1
(C)
4
2
x
3
2. (1,0 ®iÓm)
Täa ®é giao ®iÓm M cña (∆) vµ (∆') lµ nghiÖm cña hÖ:
2x y 5 0
x2y100.
+−=
⎧
⎨−−=
⎩
⇔ x4
y 3. Suy ra M(4; 3).
=
⎧
⎨=− −
⎩
Täa ®é ®iÓm I'( '
I
x; '
I
y) tháa m·n hÖ:
I'
I'
I' I'
1x 4x7
2
3y y 9.
3
2
+
⎧=
⎪=
⎧
⎪⇔
⎨⎨
+=−
⎩
⎪=−
⎪
⎩
§iÓm cÇn t×m: I' (7; −9).
0,25
0,25
0,25
0,25
C©u 4
(2,0 ®iÓm)
1. (1.0 ®iÓm)
Täa ®é ®iÓm G: G (1; 1; 1).=
VÐc t¬ chØ ph−¬ng cña ®−êng th¼ng AG: GA (3; 2; 1)=
J
JJG
.
Ph−¬ng tr×nh ®−êng th¼ng cÇn t×m : x1 y1 z1
.
321
−−−
==
2. (1,0 ®iÓm)
Ph−¬ng tr×nh theo ®o¹n ch¾n cña (BCD): xyz
333
++ = 1⇔xyz30.++−=
Kho¶ng c¸ch tõ ®iÓm A ®Õn (BCD): 4323
d(A,(BCD)) 2 3.
111
++−
==
++
Gäi R lµ b¸n kÝnh mÆt cÇu cÇn t×m, ta cã: R =d(A,(BCD)) .
Ph−¬ng tr×nh mÆt cÇu cÇn t×m: 222
(x 4) (y 3) (z 2) 12.−+−+−=
0,25
0,25
0,50
0,25
0,25
0,25
0,25
C©u 5
(1,0 ®iÓm)
Sè h¹ng thø k+1 trong khai triÓn nhÞ thøc Niut¬n:
k5kk
k1 5
TC(2x)x
−−
+=
k5k52k
5
C2 x
−−
= (k 0,1,...,5)=.
Tk+1 chøa x3 ⇔ 5 − 2k = 3 ⇔ k = 1.
Sè h¹ng cÇn t×m : 143
5
C2x = 3
80x .
0,25
0,25
0,25
0,25
……...HÕt...