
Thái Minh Tín
L p QLDD A2ớ
Tr ng DH C n Thườ ầ ơ
GI I THI UỚ Ệ
Ệá
X lý thông tin không gian là m t trong nh ng ch c năng chính c a GIS.ử ộ ữ ứ ủ
Ti n trình x lý d li u không gian đ c th c hi n b i các phép toán phânế ử ữ ệ ượ ự ệ ở
tích trên m t l p và phân tích trên nhi u l p d li u.ộ ớ ề ớ ữ ệ
Phân tích m t l p th ng đ c th c hi n tr c khi ti n hành phân tíchộ ớ ườ ượ ự ệ ướ ế
nhi u l p.ề ớ
Phép toán phân tích m t l p còn đ c g i là phép toán phân tích ngang.ộ ớ ượ ọ
B i vì trong quá trình phân tích ch x lý trên 1 l p d li u đ u vào.ở ỉ ử ớ ữ ệ ầ
L p d li u đ c x lý ch ch a m t ki u đ i t ng duy nh tớ ữ ệ ượ ử ỉ ứ ộ ể ố ượ ấ
(đi m/đ ng/vùng).ể ườ
Phép toán phân tích 1 l p đ c chia thành 3 nhóm: X lý đ i t ng, ch nớ ượ ử ố ượ ọ
đ i t ng và phân lo i đ i t ng.ố ượ ạ ố ượ
I. X LÝ Đ I T NGỬ Ố ƯỢ
1. X lý vùng ranhử
Clip:
Phép k p: t o đ u ra ch a 1 ph n c a b n đ g c.ẹ ạ ầ ứ ầ ủ ả ồ ố
Phép này gi l i t t c các y u t thu c tính t b n đ g c n m trongữ ạ ấ ả ế ố ộ ừ ả ồ ố ằ
ranh gi i c a vùng k p.ớ ủ ẹ
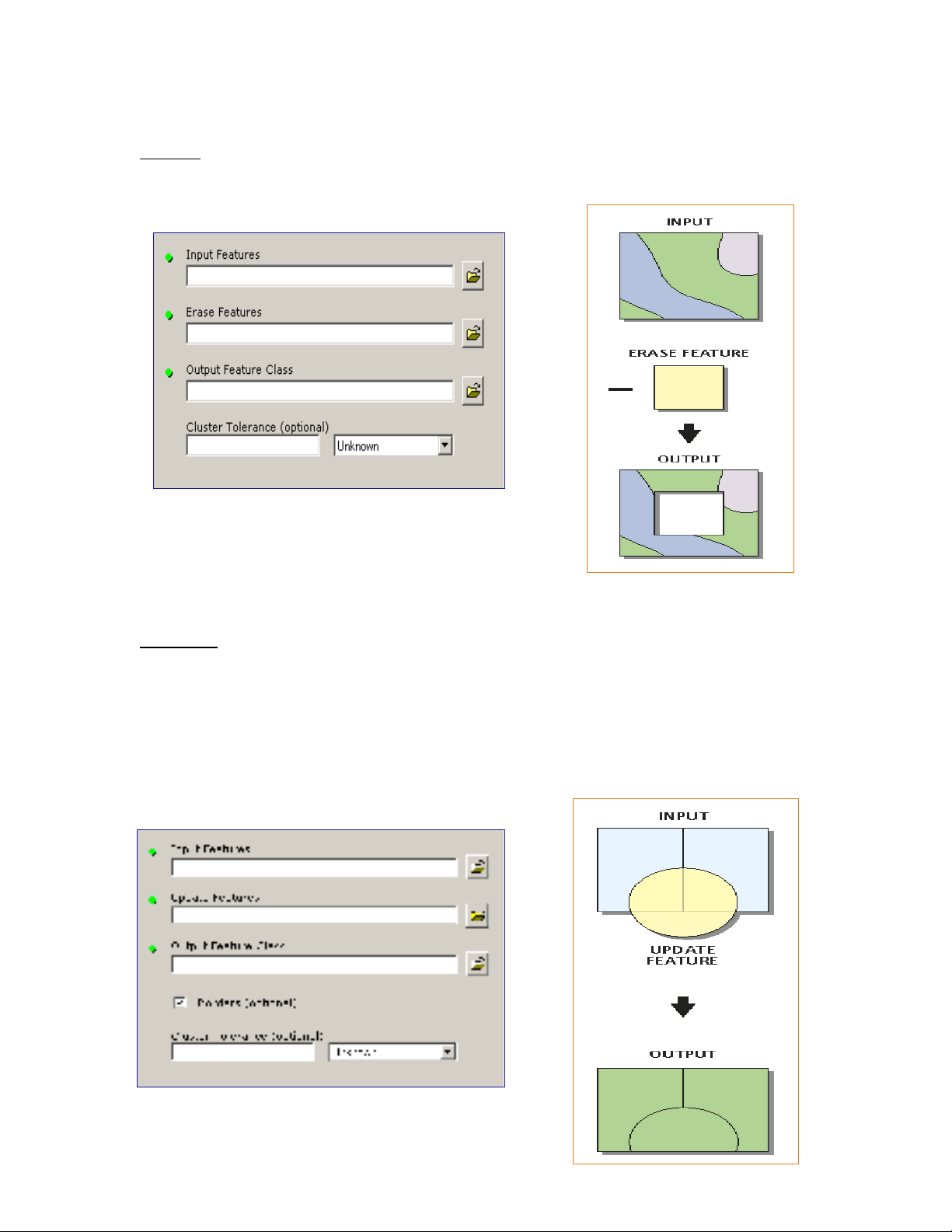
Erase:
Phép xoá: ng c l i v i phép k p.ượ ạ ớ ẹ
Phép xoá lo i b ph n n m trong vùng xoá và gi nguyên nh ng ph nạ ỏ ầ ằ ữ ữ ầ
còn l i t b n đ g c.ạ ừ ả ồ ố
Update:
Phép c p nh t: thay th d li u không gian t i m t s khu v c nh t đ nhậ ậ ế ữ ệ ạ ộ ố ự ấ ị
trên b n đ b ng m t l p m i ho c đã đ c đính chính.ả ồ ằ ộ ớ ớ ặ ượ
Phép này t o đ u ra b ng vi c s d ng l nh c t-dán.ạ ầ ằ ệ ử ụ ệ ắ
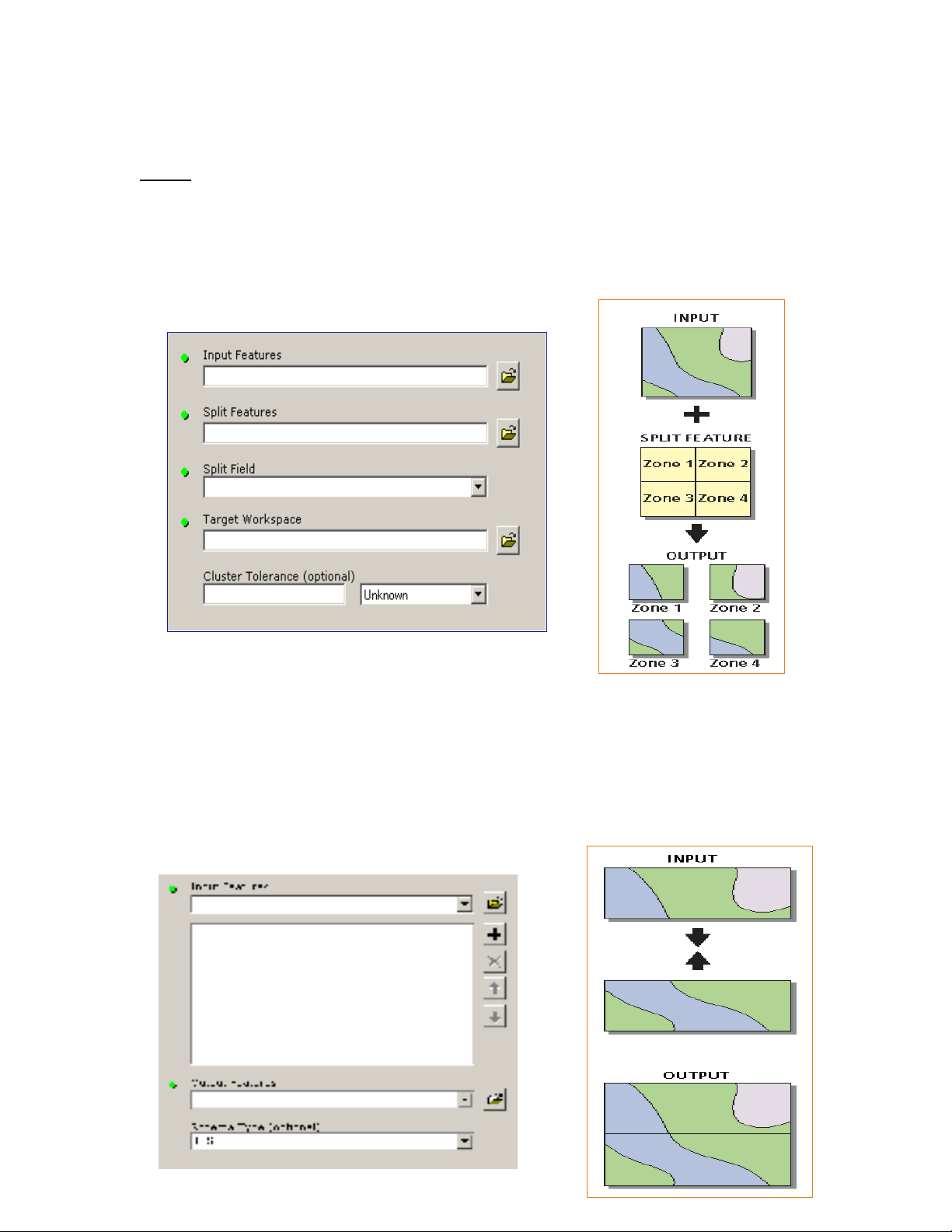
Spit:
Phép phân chia: t o ranh gi i chia b n đ ra làm nhi u khu v c.ạ ớ ả ồ ề ự
Phép này r t h u d ng khi ta c n chia m t c s d li u l n ra làm nhi uấ ữ ụ ầ ộ ơ ở ữ ệ ớ ề
ph n nh h n đ x lý.ầ ỏ ơ ể ử
Append/Mapjoin:
Phép k t n i:ế ố dùng đ k t h p nhi u b n đ nh , li n k đ t o ra m tể ế ợ ề ả ồ ỏ ề ề ể ạ ộ
b n đ l n h n.ả ồ ớ ơ
Phép này ng c v i phép phânượ ớ
chia.
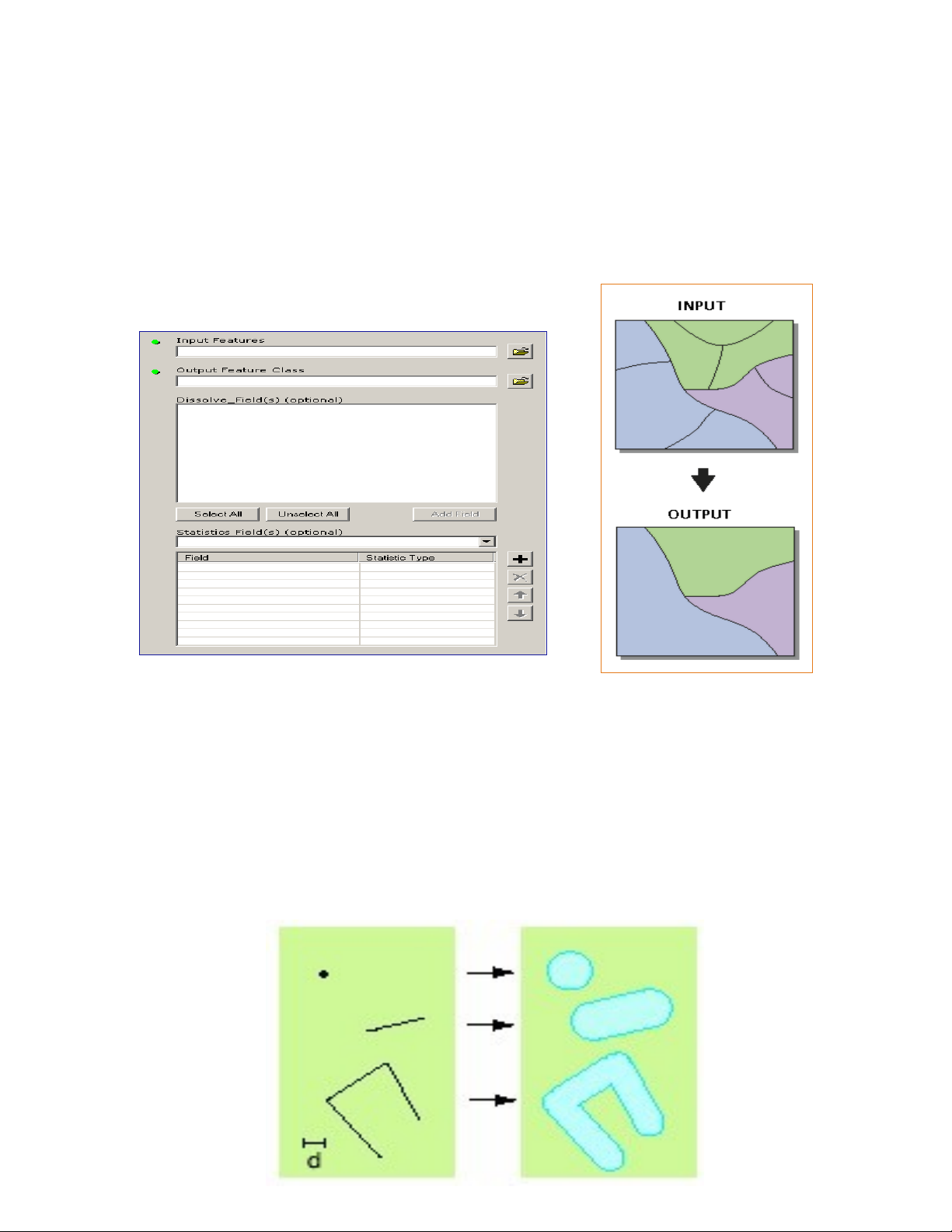
Dissolve:
Phép hoà tan: đ c dùng đ xoá b các ranh gi i không c n thi t sau khiượ ể ỏ ớ ầ ế
đã k t n i các vùng li n k có cùng tính ch t.ế ố ề ề ấ
Phép này cũng có tác d ng xoá b đi m nút (node) gi a các đ ng cóụ ỏ ể ữ ườ
cùng thu c tính.ộ
2. T o vùng lân c n: T o vùng đ m, vùng Thiesenạ ậ ạ ệ .
Th c hi n trên c s giá tr kho ng cách tính t các đ i t ng đ c ch n.ự ệ ơ ở ị ả ừ ố ượ ượ ọ
a. T o vùng đ m (buffer): ạ ệ
Vùng đ m (Buffer zone): Bên trong đ ng biên thì g i là lõi còn bên ngoàiệ ườ ọ
đ ng biên thì g i là vùng đ m (buffer). ườ ọ ệ
Cho tr c m t đ i t ng và m t giá tr kho ng cách, phép toán buffer sướ ộ ố ượ ộ ị ả ẽ
t o ra m t vùng đ m là m t polygon bao ph xung quanh t t c các đi m màạ ộ ệ ộ ủ ấ ả ể
kho ng cách t chúng đ n đ i t ng nh h n ho c b ng kho ng cách đ ra.ả ừ ế ố ượ ỏ ơ ặ ằ ả ề
Hình: T o vùng đ m cho đ i t ngạ ệ ố ượ
Vùng đ m đ c t o thành s xác l p các vùng bên trong ho c bên ngoàiệ ượ ạ ẽ ậ ặ
vùng đ m c a m i đ i t ng. ệ ủ ỗ ố ượ
ợ Vùng bao
quanh đi mể
ể Vùng bao
quanh đ ngườ
ờ Vùng bao
quanh vùng
Đây là m t phép ch n l c đ i t ng không gian đ c s d ng ph bi nộ ọ ọ ố ượ ượ ử ụ ổ ế
trong GIS.
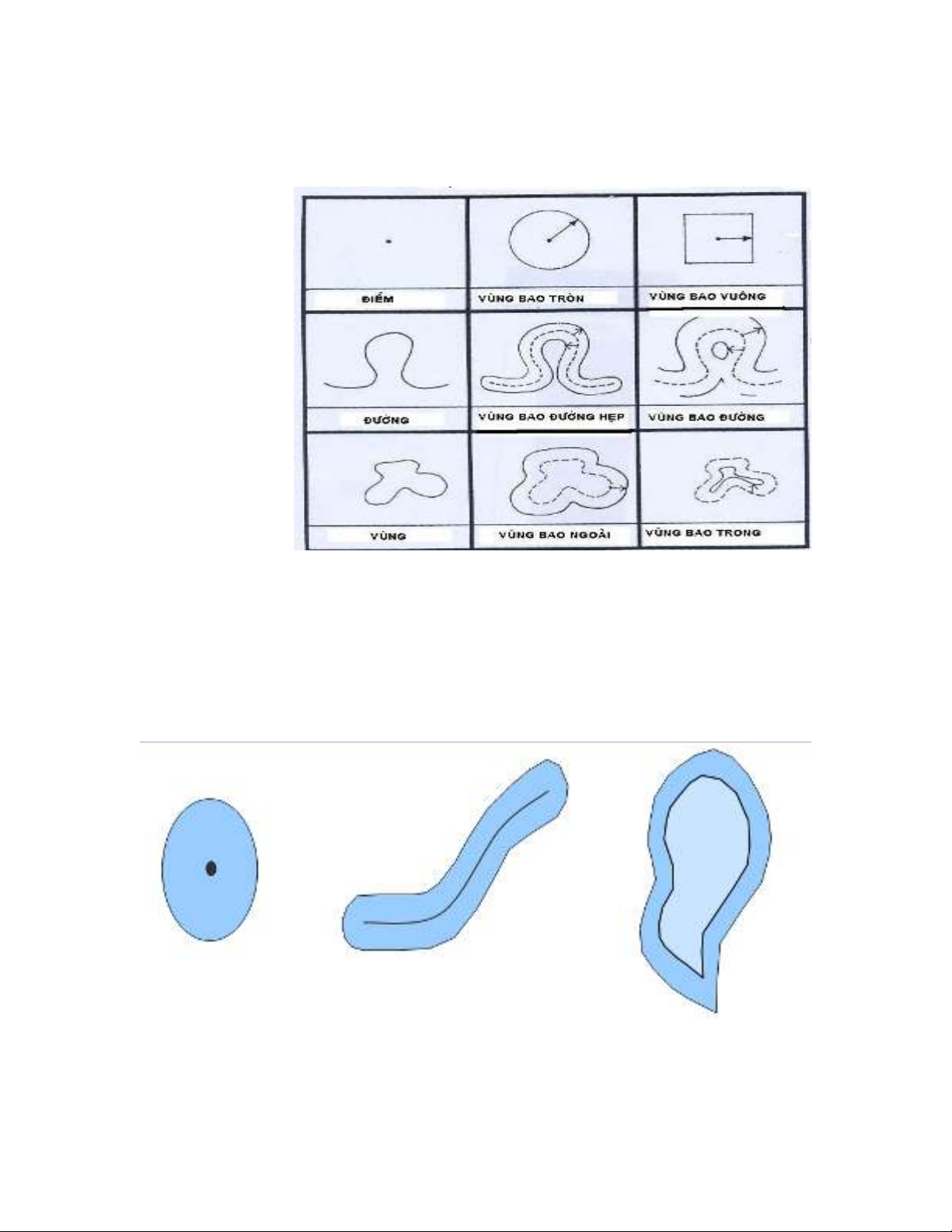
Các buffer bao quanh m t đi m có d ng vùng hình tròn, quanh m t đ ngộ ể ạ ộ ườ
có d ng vùng ngo n ngoèo và quanh m t vùng có d ng vùng r ng l n h n.ạ ằ ộ ạ ộ ớ ơ
Hình: Bi u di n các vùng bên trong ho c ngoài vùng đ m c aể ễ ặ ệ ủ
m i đ i t ngỗ ố ượ
Hình: Buffer đi mểHình: Buffer đ ngườ Hình: Buffer vùng


























