
Chuyên đ dòng đi n xoay chi u ề ệ ề
I. CÔNG SU TẤ:
Công su t c a dòng đi n xoay chi uấ ủ ệ ề : P = UIcos = I2R =
2
2
Z
RU
.
- H s công su t: cosệ ố ấ =
Z
R
=
R
U
U
- Ý nghĩa c a h s công su t cosủ ệ ố ấ
+ Tr ng h p ườ ợ cos
= 1 t c là ứ = 0: m ch ch có R, ho c m ch RLC có c ng h ng đi n (Zạ ỉ ặ ạ ộ ưở ệ L = ZC)
thì
P = Pmax = UI =
R
U2
= I2R
+ Tr ng h p ườ ợ cos
= 0 t c là ứ =
2
: M ch ch có L, ho c ch có C, ho c có c L và C mà khôngạ ỉ ặ ỉ ặ ả
có R thì P = Pmin = 0.
- R tiêu th năng l ng d i d ng to nhi t, Zụ ượ ướ ạ ả ệ L và ZC không tiêu th năng l ng c a ngu n đi n xoayụ ượ ủ ồ ệ
chi u.ề
* Đ nâng cao h s công su t c a m ch b ng cách m c thêm vào m ch cu n c m ho c t đi n thíchể ệ ố ấ ủ ạ ằ ắ ạ ộ ả ặ ụ ệ
h p sao cho c m kháng và dung kháng c a m ch x p xĩ b ng nhau đ cosợ ả ủ ạ ấ ằ ể 1.
Đi v i các đng c đi n, t l nh, … nâng cao h s công su t cosố ớ ộ ơ ệ ủ ạ ệ ố ấ đ gi m c ng đ dòng đi n.ể ả ườ ộ ệ
II. C S LÍ THUY T Đ GI I BÀI TOÁN H P ĐENƠ Ở Ế Ể Ả Ộ
1. Các công th cứ.
+ N u gi s : i = Iế ả ử 0cost
thì hi u đi n th hai đu m ch đi n Uệ ệ ế ầ ạ ệ AB = Uocos(t + )
+ C m kháng: ZảL = L
+ Dung kháng: ZC =
C
1
+ T ng tr Z = ổ ở
2
CL
2)ZZ(R
+ Đnh lu t Ôm: I = ị ậ
Z
U
I
Z
U0
0
+ Đ l ch pha gi a u và i: tgộ ệ ữ =
R
ZZ CL
+ Công su t to nhi t: P = UIcosấ ả ệ = I2R
H s công su t: K = cosệ ố ấ =
Z
R
UI
P
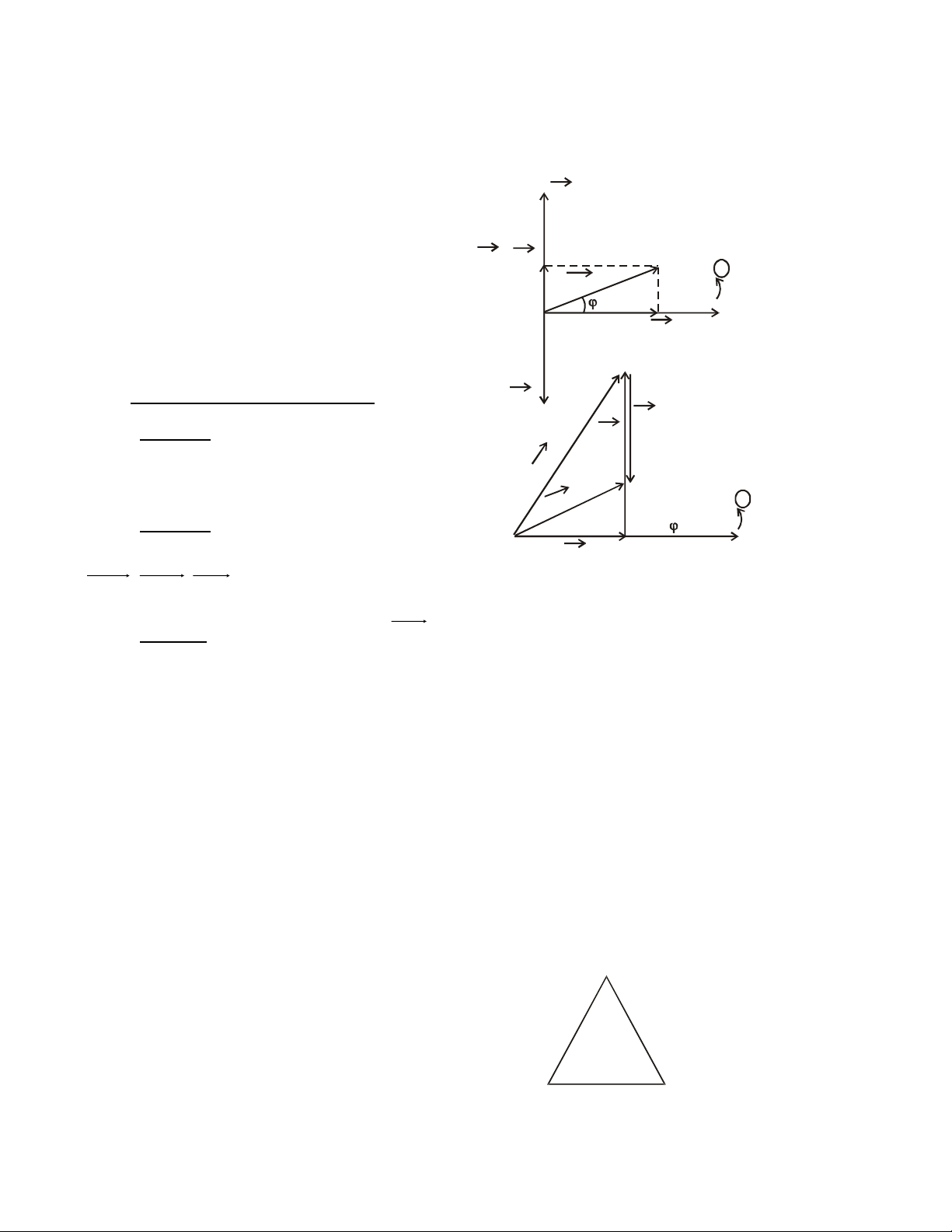
2. Gi n đ véc tả ồ ơ
1
A
B
C
b
a
c
Chuyên đ dòng đi n xoay chi u ề ệ ề
* C s :ơ ở
+ Vì dòng đi n lan truy n v i v n t c c 3.10ệ ề ớ ậ ố ỡ 8m/s nên trên m t đo n m ch đi n không phânộ ạ ạ ệ
nhánh t i m i th i đi m ta coi đ l n và pha c a c ng đ dòng đi n là nh nhau t i m i đi m.ạ ỗ ờ ể ộ ớ ủ ườ ộ ệ ư ạ ọ ể
+ Hi u đi n th t c th i hai đu đo n m chệ ệ ế ứ ờ ở ầ ạ ạ uAB = uR + uL + uC
* Cách v gi n đ véc tẽ ả ồ ơ
Vì i không đi nên ta ch n tr cổ ọ ụ
c ng đ dòng đi n làm tr c g c, g c t iườ ộ ệ ụ ố ố ạ
đi m O, chi u d ng là chi u quay l ngể ề ươ ề ượ
giác.
3. Cách v gi n đ véc t tr tẽ ả ồ ơ ượ
B c 1:ướ Ch n tr c n m ngang làọ ụ ằ
tr c dòng đi n, đi m đu m ch làm g cụ ệ ể ầ ạ ố
(đó là đi m A).ể
B c 2:ướ Bi u di n l n l t hi uể ễ ầ ượ ệ
đi n th qua m i ph n b ng các véc tệ ế ỗ ầ ằ ơ
NB; MN ;AM
n i đuôi nhau theo nguyên t c: R - đi ngang; L - đi lên; C - đi xu ng.ố ắ ố
B c 3:ướ N i A v i B thì véc t ố ớ ơ
AB
chính là bi u di n uể ễ AB
Nh n xét:ậ
+ Các hi u đi n th trên các ph n t đc bi u di n b i các véc t mà đ l n c a các véc t tệ ệ ế ầ ử ượ ể ễ ở ơ ộ ớ ủ ơ ỷ
l v i hi u đi n th hi u d ng c a nó.ệ ớ ệ ệ ế ệ ụ ủ
+ Đ l ch pha gi a các hi u đi n th là góc h p b i gi a các véc t t ng ng bi u di nộ ệ ữ ệ ệ ế ợ ở ữ ơ ươ ứ ể ễ
chúng.
+ Đ l ch pha gi a hi u đi n th và c ng đ dòng đi n là góc h p b i véc t bi u di n nó ộ ệ ữ ệ ệ ế ườ ộ ệ ợ ở ơ ể ễ
v i tr c iớ ụ
+ Vi c gi i bài toán là nh m xác đnh đ l n các c nh và góc c a tam giác d a vào các đnh lýệ ả ằ ị ộ ớ ạ ủ ự ị
hàm s sin, hàm s cosin và các công th c toán h c.ố ố ứ ọ
Trong toán h c m t tam giác s gi iọ ộ ẽ ả
đc n u bi t tr c ba (hai c nh 1 góc, haiượ ế ế ướ ạ
góc m t c nh, ba c nh) trong sáu y u t (3ộ ạ ạ ế ố
góc và 3 c nh).ạ
Đ làm đc đi u đó ta s d ng đnh lý hàm s sin ho c ể ượ ề ử ụ ị ố ặ Cosin.
2
U
AB
i
+
U
AN
U
L
U
C
U
R
AM
B
N
UL
UR
UA B
O
U +LUC
UC
i
+

D NG 1Ạ: Tính công su t tiêu th b i đo n m ch đi n xoayấ ụ ở ạ ạ ệ
ề
Chuyên đ dòng đi n xoay chi u ề ệ ề
+
SinC
a
SinB
b
¢Sin
a
+ a2 = b2 + c2 - 2bccosA
b2 = a2 + c2 - 2accosB
c2 = a2 + b2 - 2abcosC
Cách gi iả:
- Áp d ng các công th c:ụ ứ
+ Công th c t ng quát tính công su t: ứ ổ ấ
cosP UI
ϕ
=
+ V i đo n m ch RLC không phân nhánh, có th tính công su t b i: ớ ạ ạ ể ấ ở
P UI=
cos
ϕ
+ H s công su t (đo n m ch không phân nhánh): ệ ố ấ ạ ạ
cos P R
UI Z
ϕ
= =
Bài t p ậ
T LU NỰ Ậ :
Bài 1: M c n i ti pắ ố ế v i cu n c m ớ ộ ả có r i m c vào ngu n xoay chi u. Dùng ồ ắ ồ ề vônk có ếr t ấ
l n đo ớ hai đu cu n c m, ở ầ ộ ả đi n trệ ở và c đo n m ch ta có các giá tr t ng ng là 100V, 100V, ả ạ ạ ị ươ ứ
173,2V. Suy ra h s công su tệ ố ấ c a cu n c mủ ộ ả
Bài gi iả
Theo bài ra :
Ta có:
H s công su tệ ố ấ c a cu n c m: ủ ộ ả
0
0 0
0
50
cos 0,5
100
R
LR LR
U
R
Z U
ϕ
= = = =
Bài 2: Đt m t ặ ộ hi u đi n th xoay chi uệ ệ ế ề có t n s gócầ ố vào hai đu cu n dây cóầ ộ R, L thì công su t ấ
tiêu thụ c a đo n m ch là Pủ ạ ạ 1. N u n i ti p v i cu n dây m t ế ố ế ớ ộ ộ t đi nụ ệ C v i ớ
2
2 1LC
ω
=
và đt vào ặhi uệ
đi n thệ ế trên thì công su t tiêu thấ ụ là P2. Tính giá tr c a Pị ủ 2
Bài gi iả
C ng đ dòng đi n tr c khi m c t đi n C: ườ ộ ệ ướ ắ ụ ệ
12 2
L
U
I
R Z
=+
3

Chuyên đ dòng đi n xoay chi u ề ệ ề
C ng đ dòng đi n sau khi m c thêm t đi n C là: ườ ộ ệ ắ ụ ệ
22 2
( )
L C
U
I
R Z Z
=+ −
Do
2
2 1 2 L C
LC Z Z
ω
= =�
Suy ra
22 2
( )
L
U
I
R Z
=+ −
Suy ra I2=I1 P2=P1
Bài 3 : Cho m t đo n m ch đi n g m m t bi n tr R ộ ạ ạ ệ ồ ộ ế ở m c n i ti pắ ố ế v i m t ớ ộ t đi nụ ệ có đi n dungệ
. Đt vào hai đu đo n m ch m t ặ ầ ạ ạ ộ hi u đi n th xoay chi uệ ệ ế ề v i ớt n s gócầ ố .
Thay đi R ta th y v i hai giá tr c a ổ ấ ớ ị ủ thì công su tấ c a đo n m ch đu b ng nhau. Tíchủ ạ ạ ề ằ
b ng:ằ
Bài gi iả
Khi
Khi
Vì và
V i: ớ
Bài 4: Cho đo n m ch đi n xoay chi u RLC m c n i ti p. Đt vào hai đu m ch m t hi u đi nạ ạ ệ ề ắ ố ế ặ ầ ạ ộ ệ ệ
th n đnh u = Uế ổ ị o cos(2ft). V đ th bi u di n s bi n đi c a công su t tiêu th P c a đo n m chẽ ồ ị ể ễ ự ế ổ ủ ấ ụ ủ ạ ạ
đi n khi cho đi n tr R c a đo n m ch thay đi t 0 ệ ệ ở ủ ạ ạ ổ ừ
Bài gi i:ả
+ Công su t tiêu th :ấ ụ
bR
aR
)ZZ(R
RU
RIP
22
CL
2
2
2
+ L y đo hàm c a P theo R:ấ ạ ủ
22
)bR(
)Rb(a
'P
P' = 0 R =
b
+ L p b ng bi n thiên:ậ ả ế
+ Đ th c a P theo Lồ ị ủ
4
L
P'
P
0
b
0
+
Pmax
00
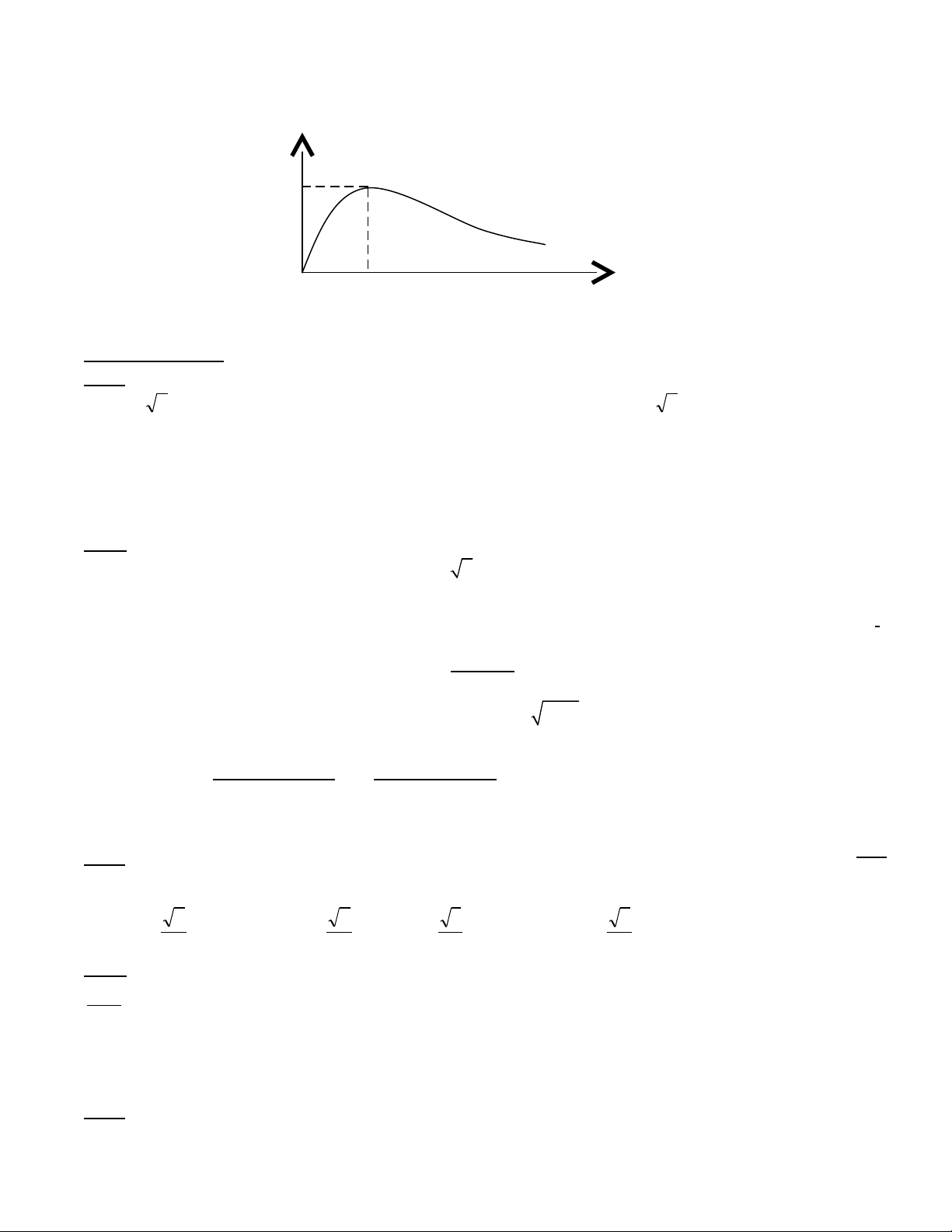
R
O
P
Pmax
R =
Chuyên đ dòng đi n xoay chi u ề ệ ề
TR C NGHI M:Ắ Ệ
Bài 1: Ch n câu ọđúng. Hi u đi n th gi a hai đu m t đo n m ch xoay chi u là: ệ ệ ế ữ ầ ộ ạ ạ ề
u = 100
2
cos(100t - /6)(V) và c ng đ dũng đi n qua m ch là i = 4ườ ộ ệ ạ
2
cos(100t - /2)(A). Công
su t tiêu th c a đo n m ch đó là:ấ ụ ủ ạ ạ
A. 200W. B. 600W. C. 400W. D. 800W.
CH N AỌ
Bài 2: Cho m ch đi n xoay chi u RLC ạ ệ ề m c n i ti pắ ố ế , có R là bi n tr . Đt vào hai đu đo n m chế ở ặ ầ ạ ạ
hi u đi n th xoay chi uệ ệ ế ề có bi u th c ể ứ
120 2 cos(120 )u t
π
=
V. Bi t r ng ng v i hai giá tr c a bi nế ằ ứ ớ ị ủ ế
tr :Rở1=18
Ω
,R2=32
Ω
thì công su t tiêu thấ ụ P trên đo n mach nh nhau. ạ ư Công su tấ c a đo n m ch cóủ ạ ạ
th nh n giá tr nào sau đây: A.144Wể ậ ị B.288W C.576W D.282W
Bài gi iả
Áp d ng công th c:ụ ứ
2
1 2 ( )
L C
R R Z Z= −
1 2 24
L C
Z Z R R− = = Ω�
V y ậ
1
2 2
1 2
2 2 2 2
2
288
( ) ( )
L C L C
U U
P R R W
R Z Z R Z Z
= = =
+ − + −
CH N BỌ
Bài 3: Khi đt m t hi u đi n th u = 120cos200t (V) vào hai đu đo n m ch g m cu n dây có L = ặ ộ ệ ệ ế ầ ạ ạ ồ ộ
200
R
.
Khi đó h s công su t c a m ch là:ệ ố ấ ủ ạ
A.
2
2
B.
4
2
C.
2
3
D.
3
3
Bài 4: Đt m t hi u đi n th u = 250cos(100ặ ộ ệ ệ ế
t
)V vào hai đu đo n m ch g m cu n c m có L =ầ ạ ạ ồ ộ ả
0.75 H
π
và đi n tr thu n R m c n i ti p.Đ công su t c a m ch có giá tr P =125W thì R có giá tr ệ ở ầ ắ ố ế ể ấ ủ ạ ị ị
A. 25
B. 50
C. 75
D. 100
CH N AỌ
Bài 5: M t m ch xoay chi u R,L,C không phân nhánh trong đó R= 50ộ ạ ề , đt vào hai đu m ch m t hi u đi nặ ầ ạ ộ ệ ệ
th U=120V, fế0 th i l ch pha v i u m t gỡ ệ ớ ộ óc 600, c ng su t c a m ch làụ ấ ủ ạ
5
CH N AỌ


























