MÔ PHỎNG VÀ NGHIÊN CỨU TƯƠNG TÁC SÓNG
VÀ ĐÊ NGẦM CHẮN SÓNG
TS. Phùng Đăng Hiếu
Bộ môn Hải dương học, Trường Đại học Khoa học Tự nhiên, ĐHQG Hà nội
1. Giới thiệu
Hiểu được các tương tác giữa sóng và công trình biển nói chung, sóng và đê
ngầm chắn sóng nói riêng là một vấn đề rất khó nhưng lại có ý nghĩa lớn trong thiết kế
hiệu quả các công trình trên biển. Sóng tương tác với công trình trong vùng ven bờ
thường rất phức tạp do tính chất kết hợp phi tuyến của nhiều quá trình thuỷ động lực.
Thông thường để hiểu rõ các tương tác sóng và một công trình cụ thể dự kiến sẽ xây
dựng thì các nhà thiết kế kỹ thuật phải thực hiện thí nghiệm đối với mô hình mẫu thu
nhỏ trong các máng thí nghiệm sóng trong phòng thí nghiệm cùng với sự trợ giúp của
các thiết bị đo áp suất, nồng độ bùn cát, vận tốc dòng chảy, v.v., do đó các chi phí khá
tốn kém. Trên thực tế các kết quả của thí nghiệm vật lý cũng còn chưa hoàn toàn tin
cậy do còn một số hạn chế như hiệu ứng tỷ lệ thu nhỏ, ảnh hưởng không thật của các
sóng phản xạ giả từ máy tạo sóng của máng sóng, v.v.. Trong một số năm gần đây, với
sự phát triển nhanh của tốc độ máy tính cộng với sự trợ giúp của các phương pháp số
hiện đại, khái niệm thí nghiệm số đã dần dần phổ biến trong một số ngành nghiên cứu
ứng dụng, trong đó có lĩnh vực kỹ thuật công trình và môi trường biển.
Trong nghiên cứu trình bày ở đây sẽ đề cập đến việc phát triển và ứng dụng mô
hình toán mô phỏng và nghiên cứu các tương tác giữa sóng và đê ngầm chắn sóng. Mô
hình số dựa trên việc giải số hệ phương trình Navier-Stokes mở rộng cho môi trường
xốp cùng với sự trợ giúp của phưng pháp VOF (Volume Of Fluid) hiện đại (Hiếu và
nnk, 2004), được ứng dụng vào nghiên cứu các tương tác của sóng và công trình xốp.
Trước tiên mô hình số được tính toán kiểm nghiệm với việc mô phỏng tương tác phi
tuyến trong hệ sóng đứng có so sánh với nghiệm lý thuyết của Goda (1968); Tính toán
kiểm nghiệm cũng được thực hiện cho trường hợp truyền sóng và sóng đổ trên sườn
thoải có đê ngầm xốp. Các kết quả được so sánh với các số liệu thí nghiệm đã được
xuất bản. Sau đó mô hình toán được áp dụng nghiên cứu tương tác sóng và đê xốp
ngầm. Kết quả mô phỏng số cho thấy tồn tại một phạm vi giới hạn hiệu quả của độ xốp
của đê ngầm cho phép chắn sóng hiệu quả nhất. Các kết quả của nghiên cứu cũng gợi
ý cho thấy có khả năng xây dựng một máng sóng thí nghiệm số phục vụ cho nghiên
cứu và thiết kế các công trình biển.
2. Mô hình toán
2.1. Hệ phương trình cơ bản
Dựa trên hệ phưng trình Navier-Stokes, Sakakiyama và Kajima (1992) đã phát
triển hệ phương trình mở rộng cho dòng rối không ổn định trong môi trường xốp,
trong đó sức cản của môi trường xốp được mô hình hoá bằng ứng lực kéo và lực quán
tính. Trong nghiên cứu này giả thiết chất lỏng không nén, mô hình 2D bao gồm
Tuyển tập báo cáo Hội thảo khoa học lần thứ 10 - Viện KH KTTV & MT 211
phương trình liên tục và các phương trình Navier-Stokes mở rộng cho môi trường xốp
của Sakakiyama và Kajima (1992) được sử dụng làm hệ phương trình xuất phát mô tả
chuyển động của chất lỏng:
Phương trình liên tục:
v
zx q
z
w
x
u
γ
γ
γ
=
∂
∂
+
∂
∂
(1)
Phương trình Navier-Stokes mở rộng (theo phương x và z):
uxxezex
v
z
x
vqRuD
x
w
z
u
zx
u
xx
p
z
wu
x
uu
t
u+−−
⎭
⎬
⎫
⎩
⎨
⎧⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
∂
∂
+
⎭
⎬
⎫
⎩
⎨
⎧⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
+
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
νγνγ
ρ
γ
λ
λ
λ
2 (2)
wvzzezex
vzx
vqgRwD
z
w
zz
u
x
w
xz
p
z
ww
x
uw
t
w+−−−
⎭
⎬
⎫
⎩
⎨
⎧⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
+
⎭
⎬
⎫
⎩
⎨
⎧⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
∂
∂
+
∂
∂
−=
∂
∂
+
∂
∂
+
∂
∂
γνγνγ
ρ
γλλ
λ
2 (3)
trong đó t: thời gian; x và z: toạ độ ngang và đứng; u, w: thành phần vận tốc theo phương
ngang và đứng;
ρ
: mật độ chất lỏng; p: áp suất;
ν
e: hệ số nhớt (tổng của hệ số nhớt phân
tử và nhớt rối); g: gia tốc trọng trường;
γ
v: độ xốp;
γ
x,
γ
z: độ xốp chiếu lên phương z và x;
: hàm nguồn tạo sóng; q
qu, qw: hàm nguồn trên phương x và z; Dx, Dz: các hệ số tiêu tán
năng lượng trên phương x và z; Rx, Rz: lực cản do môi trường xốp. Các hệ số
λ
v,
λ
x,
λ
z
được định nghĩa như sau:
(
)
()
()
⎪
⎭
⎪
⎬
⎫
−+=
−+=
−+=
Mzzz
Mxxx
Mvvv
C
C
C
γγλ
γγλ
γγλ
1
1
1
(4)
ở đây CM là hệ số quán tính.
Các lực cản Rx và Rz được xác định như sau:
()
22
1
2
1wuu
x
C
Rx
D
x+−
∆
=
γ
(5)
()
22
1
2
1wuw
z
C
Rz
D
z+−
∆
=
γ
(6)
với ∆x, ∆z là các kích thước ngang và đứng của lưới tính; CD là hệ số cản.
Các hàm nguồn được xác định như sau:
(7)
⎩
⎨
⎧
= 0
s
q
qtại nguồn
chỗ khác
uqqu
=
(8)
wqqw
=
(9)
2.2. Biên mặt tự do
Để áp dụng hệ phưng trình xuất phát cho miền bao gồm cả pha lỏng và khí thì
cần có sự xử lý đặc biệt cho biên giữa nước và khí tức là biên bề mặt tự do. Do chất
lỏng giả thiết là không nén nên mật độ là không đổi trong vùng khí và trong vùng nước.
Để phân biệt hai vùng này phưng pháp VOF (Hirt và Nichols, 1981) được sử dụng.
Tuyển tập báo cáo Hội thảo khoa học lần thứ 10 - Viện KH KTTV & MT
212
Trong phương pháp VOF thì hàm thể tích chất lỏng F được sử dụng để định
nghĩa vùng chất lỏng. Giá trị của là phần thể tích chất lỏng chiếm chỗ trong một ô
lưới. Cụ thể nếu = 1 có nghĩa là đầy nước, ngược lại = 0 có nghĩa là không có
nước. Ô lưới có 0< <1 chứa bề mặt phân cách nước và khí. Với định nghĩa như vậy,
ta có thể “nắm bắt” được bề mặt tự do ở mọi thời điểm bằng cách giải phương trình
tiến triển của hàm như sau:
F
FF
F
F
qF
z
Fw
x
Fu
t
Fz
xv =
∂
∂
+
∂
∂
+
∂
∂
(10)
trong đó là nguồn do biên tạo sóng sinh ra.
qF
Do tồn tại gradient rất lớn của hàm tại mặt tự do và hàm phải được bảo toàn
nên thuật toán giải phương trình (10) cũng phải được lựa chọn thích hợp sao cho khuếch tán
số phải nhỏ. Để đáp ứng điều đó, phương pháp PLIC (Hiếu, 2004) được sử dụng.
F F
2.3. Mô hình rối
Để ước lượng rối qui mô nhỏ do sóng đổ gây ra và các đóng góp của rối qui mô
dưới lưới, mô hình rối tương tự như LES (Large Eddy Simulation) được kết hợp vào
mô hình xuất phát. Hệ phương trình Navier-Stokes được lọc không gian bằng sơ đồ
Smangorinski (1963). Trong sơ đồ Smagorinsky thì động lượng trao đổi do qui mô rối
dưới lưới được truyền tải thông qua hệ số nhớt rối ( t
ν
). Hệ số nhớt rối này được xác
định như sau:
(
)
2/1
,,
2).2( zxzxst SSC ∆=
ν
(11)
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
=x
w
z
u
Szx 2
1
, (12)
(13)
2/1
)( zx∆∆=∆
với là tham số của mô hình có giá trị trong khoảng
s
C2,01,0
≤
≤
s
C
2.4. Phương pháp nguồn tạo sóng
Để giảm thiểu sự phản xạ sóng tại biên tạo sóng, phương pháp nguồn tạo sóng
của Ohyama và Nadaoka (1991) được sử dụng. Phương pháp này bao gồm hai phần
cấu tạo chính đó là hàm nguồn và lớp hấp thụ năng lượng. Hàm nguồn được thêm vào
phương trình bảo toàn khối lượng (phương trình liên tục) nhằm phát sinh sóng. Trong
khi đó thì lớp hấp thụ năng lượng được tạo ra bằng cách thêm vào phương trình
chuyển động một lực cản ma sát tỉ lệ với tốc độ của dòng chảy. Phương trình của hàm
nguồn như sau:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
+
+
∆
≤
+
+
∆
=
Tt
d
d
x
U
Tt
d
d
x
U
T
t
q
s
i
s
i
s
i
s
i
s3
2
3 if
2
3
η
η
η
η
(14)
trong đó: là hàm nguồn,
s
q
là chu kỳ sóng cần tạo, là độ sâu nước, và
di
Ui
η
là vận
tốc và dao động mặt nước được xác định bằng lý thuyết sóng Stokes bậc 3, là thời gian, ts
x
∆
là kích thước lưới tại điểm nguồn, s
η
là độ dịch chuyển thực của bề mặt nước tại điểm nguồn.
Tuyển tập báo cáo Hội thảo khoa học lần thứ 10 - Viện KH KTTV & MT 213
2.5. Phương pháp giải
Các phương trình xuất phát được sai phân hoá bằng sơ đồ sai phân hữu hạn trên
lưới xen kẽ. Các thành phần vận tốc được xác định tại cạch của ô lưới trong khi đó các đại
lượng vô hướng được xác định ở tâm của ô lưới. Phương pháp SMAC (Simplified Marker
and Cell Method) được áp dụng để dẫn ra phương trình Poisson cho thành phần hiệu
chỉnh áp suất và được giải bằng phương pháp lặp BiCGSTAB. Chi tiết về các phương
trình sai phân hoá và thuật giải có thể xem trong bài báo của Hiếu và nnk (2004).
3. Các kết quả nghiên cứu
3.1. Sóng đứng
Trước tiên, mô hình được thực hiện tính toán trường sóng đứng trên nền đáy
phẳng có độ sâu nước nông 0,4m sóng tới có độ cao 0,10 m chu kỳ 1,6s phía trước một
tường đứng. Đây là trường hợp rất đơn giản của sóng nước nông có tương tác phi
tuyến tính của sóng tới và sóng phản xạ phía trước tường đứng. Như đã biết trong các
sách giáo khoa về lý thuyết sóng phi tuyến, sóng đứng khi có tương tác phi tuyến thì
độ cao sóng tại điểm bụng lớn hơn hai lần độ cao của sóng tới và tại điểm nút thì tồn
tại các dao động sóng bậc cao dẫn đến tại điểm nút sóng không bị triệt tiêu. Năm 1968
Goda đã phát triển lý thuyết sóng Stokes bậc 3 cho tương tác sóng phi tuyến. Nghiệm
lý thuyết về sóng đứng theo lý thuyết sóng Stokes bậc 3 của Goda (1968) đã được
kiểm chứng với rất nhiều kết quả thí nghiệm vật lý và đã được khẳng định có thể mô
phỏng cực tốt trường hợp sóng đứng trên nền đáy phẳng. Trong điều kiện kiểm
nghiệm mô hình toán trong nghiên cứu này, các kết quả mô phỏng số được so sánh với
nghiệm lý thuyết của Goda (1968).
0
0.5
1
1.5
2
2.5
3
-1 -0.8-0.6 -0.4-0.20
x/L
H
/
H
I
Simulated
Theroretical (S tockes 3rd order)
Vertical w a l
l
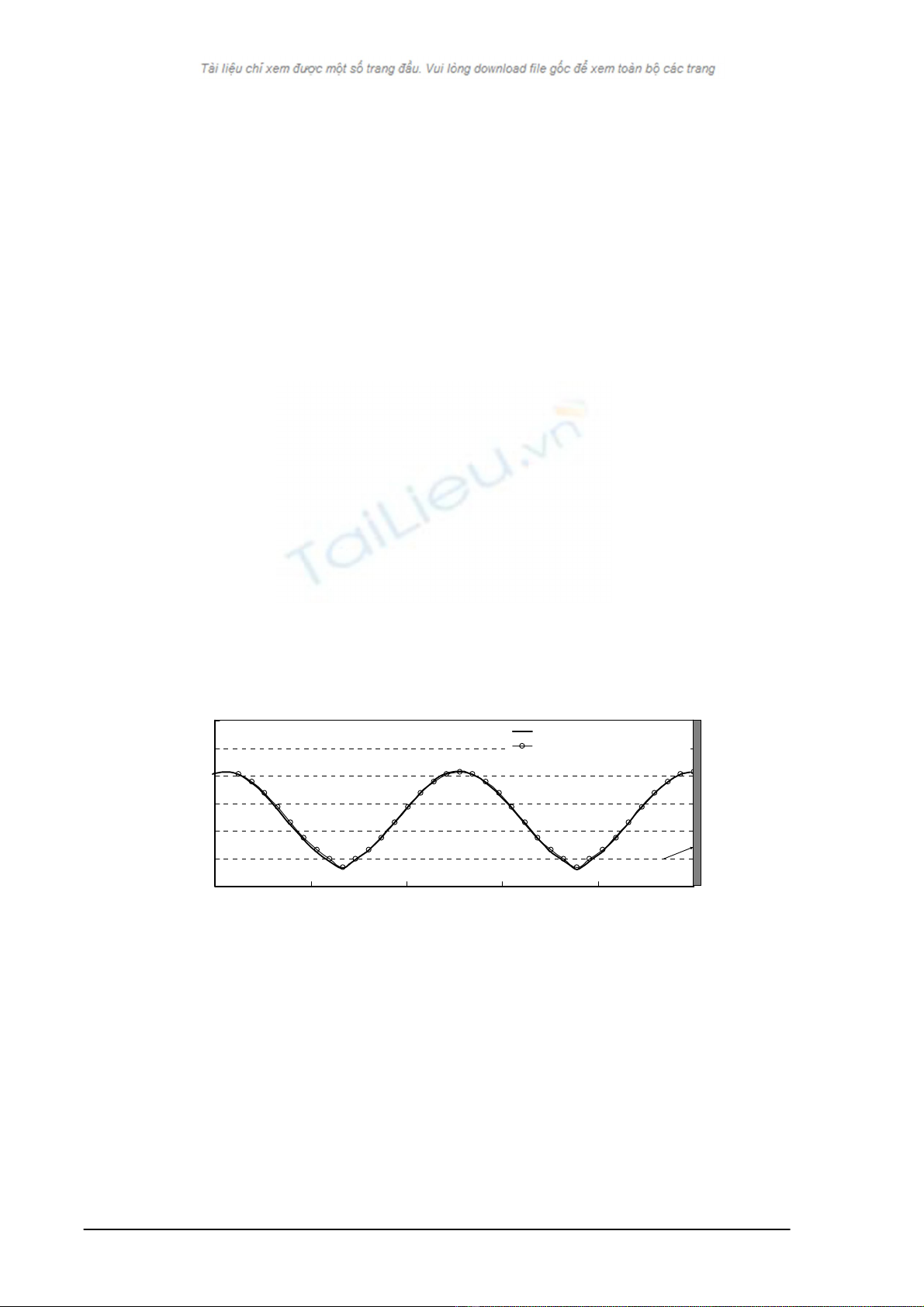
Hình 1. So sánh kết quả mô phỏng và lý thuyết cho trường hợp sóng đứng.
Trên hình 1 ta thấy rõ sự phù hợp giữa kết quả mô phỏng số và nghiệm lý
thuyết. Tính phi tuyến của tương tác sóng tới và sóng phản xạ cũng thấy rất rõ.
3.2. Tương tác sóng và đê xốp ngầm
Trong phần nghiên cứu này, thí nghiệm số được thực hiện cho trường hợp sóng
và đê xốp ngầm với điều kiện thí nghiệm số tương tự như điều kiện thí nghiệm vật lý
đã thực hiện tại phòng thí nghiệm thuỷ lực môi trường của đại học tổng hợp Saitama
Nhật bản. Máng sóng thí nghiệm có độ dài là 18m, rộng 0,4m và cao 0,7m. Một đê
Tuyển tập báo cáo Hội thảo khoa học lần thứ 10 - Viện KH KTTV & MT
214
ngầm được đặt cách bảng tạo sóng một khoảng 10,5m. Đê ngầm được làm bằng đá cục
có đường kính trung bình 0,025m, đê cao 0,33m, rộng 1,16m và có độ xốp là 0,45. Độ
sâu nước là 0,376m sóng tới có độ cao 0,092m chu kỳ 1,6s. Phía trước, trên và sau đê
ngầm có đặt 38 điểm đo sóng để phân tích ra dao động mực nước và phân bố độ cao
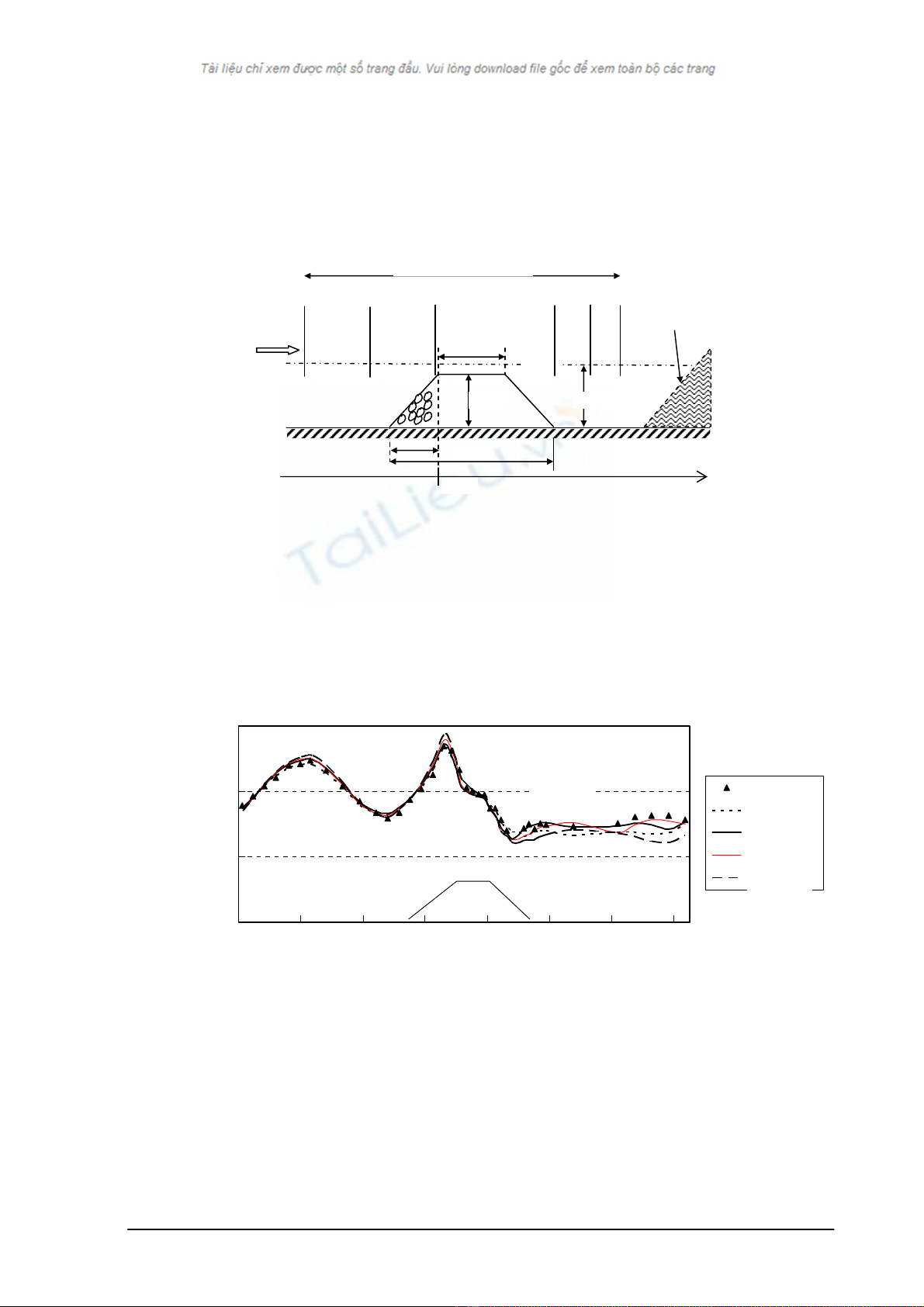
sóng. Hình 2 trình bày sơ lược điều kiện thí nghiệm, kích thước đê ngầm và các điểm
đo sóng.
Hình 2. Sơ đồ thí nghiệm sóng tương tác với đê xốp ngầm.
Do trong mô hình tồn tại các hệ số cản quán tính và hệ số ma sát nên
trước hết các hệ số này phải được khảo sát mức độ nhạy cảm của nó và cách thức nó
tác động đến kết quả mô phỏng số. Dựa vào phạm vi biến đổi của các hệ số này trong
các nghiên cứu trước đây (Sakakiyama và Kajima, 1992; Mizutani và nnk, 1996;
Karim và nnk, 2003), các giá trị của = 0,5; 1,0; 1,5; 2,0; 2,5; 3,5; 4,0 và =
0,5; 1,0; 1,5; 2,0; 2.5 được lựa chọn cho thí nghiệm khảo sát lỗi (trial-error
investigation).
M
CD
C
D
CM
C
0
0.5
1
1.5
-0.7 -0.5 -0.3 -0.1 0.1 0.3 0.5 0.7
x/L
H/HI
Measured
(Cm=0.5)
(Cm=1.0)
(Cm=1.5)
(Cm=2.0)
Lớp hấp thụ
0,43
0,30
0,33
1,16
d=0,376
SWL
Són
g
t
ới
x
=0
m
x
G38
CD =3,5
CM=0,5 )
CM=1,0 )
CM=1,5 )
CM=2,0 )
G31 G34G17 G12 G1
38 điể
m
đo són
g
Hình 3. Ảnh hưởng của hệ số cản quán tính lên phân bố độ cao sóng. Đường cong: kết quả
mô phỏng số; Tam giác đen: kết quả thí nghiệm (Hiếu, 2004).
Hình 3 trình bày các ảnh hưởng của lên phân bố độ cao sóng với giá trị cố
định của =3,5. Từ hình vẽ ta thấy thay đổi giá trị của làm ảnh hưởng đáng
kể đến phân bố độ cao sóng. Giá trị của càng cao thì phản xạ càng lớn ở phía
trước của đê ngầm. Phía sau đê phân bố của độ cao sóng biến đổ rất phức tạp theo sự
biến đổi của . Như chúng ta đã biết trong các tài liệu giáo khoa là sóng ở phía sau
vật cản như đê ngầm thì bao gồm sóng truyền qua (transmitted waves) có tần số cơ sở
M
C
D
CM
C
M
C
M
C
Tuyển tập báo cáo Hội thảo khoa học lần thứ 10 - Viện KH KTTV & MT 215