Mt s phng pháp gii phng trình a thc bc cao mt n – V ình Dng
1
CHUYÊN  BI DNG HS KHÁ , GII MÔN TOÁN
MT S PHNG PHÁP GII PHNG TRÌNH
A THC BC CAO MT N
Hn bn nghìn nm trc ây, ngi Hi Lp ã bit cách gii các phng trình
bc nht và bc hai
Phng trình bc 3
- Nm 1526 nhà toán hc I-ta-li-a là Phe-rô mi tìm c cách gii phng trình
bc 3 dng x
3
+ ax = b vi a , b > 0
- Nm 1535 nhà toán hc Tac-ta-li-a ã tìm c cách gii tng quát phng trình
x
3
+ ax + b = 0 vi mi giá tr ca a , b
- Nm 1545 nhà toán hc Các-a-nô ã công b công thc tìm nghim ca
phng trình bc ba
Phng trình bc 4
Nm 1545, nhà toán hc I-ta-li-a là phe-ra-ri ã tìm ra cách gii tng quát
phng trình bc bn
Phng trình bc cao hn 4
Trong các th k 17 và 18 các nhà toán hc ã mt rt nhiu công sc  tìm cách
gii tng quát phng trình bc 5 , bc 6 nhng không thành công
n u th k 19 thì hai nhà toán hc ngui Na-uy là A-ben và nhà toán hc
ngui Pháp là Ga-loa ã gii quyt vn  có th gii phng trình bc cao hn bn
b!ng cn thc hay không.
- A-ben ã chng minh c r!ng các phng trình bc cao hn bn di dng
tng quát không th gii c b!ng cn thc . Tc là không th biu th c các
nghim ca phng trình ó b!ng các phép toán : cng , tr" , nhân , chia , lu#
th"a và khai cn
- Còn Ga-loa ch$ ra c du hiu nhn bit mt phng trình bc cao hn bn có
th gii c b!ng cn thc hay không , b!ng mt lý thuyt c áo mà sau
này mang tên ông : lý thuyt nhóm
Mt s phng pháp gii phng trình a thc bc cao mt n – V ình Dng
2
Vy là các phng trình bc cao hn bn di dng tng không th gii c
b!ng cn thc
M%t khác i vi hc sinh lp 9 ã bit gii phng trình bc nht và bc hai
di dng tng quát . Còn cách gii tng quát ca phung trình bc ba và bc bn thì
phc tp i vi hc sinh ph thông
Nh vy không có phng pháp chung  gii tt c các phng trình bc cao
mà phi cn c vào t"ng phng trình ,  tìm các gii thích hp
Sau ây xin cp n mt s phng pháp riêng  gii phng trình a thc
bc cao hn 2, nh!m b&i d'ng hc sinh khá gi(i ca lp 9
A
AO
I. Phng pháp bin i v phng trình tích.
Mt trong các phng pháp riêng gii phng trình a thc bc cao là phân tích
a thc thành nhân t) có bc thp hn  a vic gii phng trình ã cho v gii
mt phng trình tích
Ví d 1: Gii phng trình sau: 5x
3
- 6x
2
- 2x
3
+ 3 = 0
Gii
Nhn xét : Nu phng trình trên có nghim nguyên thì s này phi là c ca 3. Ta
thy a thc 5x
3
- 6x
2
- 2x
3
+ 3 có nghim nguyên x = 1 . Vy khi phân tích a thc
này thành nhân t) thì a thc này cha nhân t) x - 1.
5x
3
- 6x
2
- 2x
3
+ 3 = 0 ⇔ 5x
3
- 5x
2
- x
2
+ x - 3x + 3 = 0 ⇔ (x - 1)(x
2
- x - 3) = 0
⇔ x- 1 = 0 ho%c x
2
- x - 3 = 0
x
2
- x - 3 = 0 ⇔ x =
 +
ho%c x =
 −
Phong trình Vy phng trình ã cho có ba nghim
x
1
= 1 x
2
=
 +
x
3
=
 −
Ví d 2: Gii phng trình : x
4
+ 12x
3
+ 32x
2
- 8x - 4 = 0
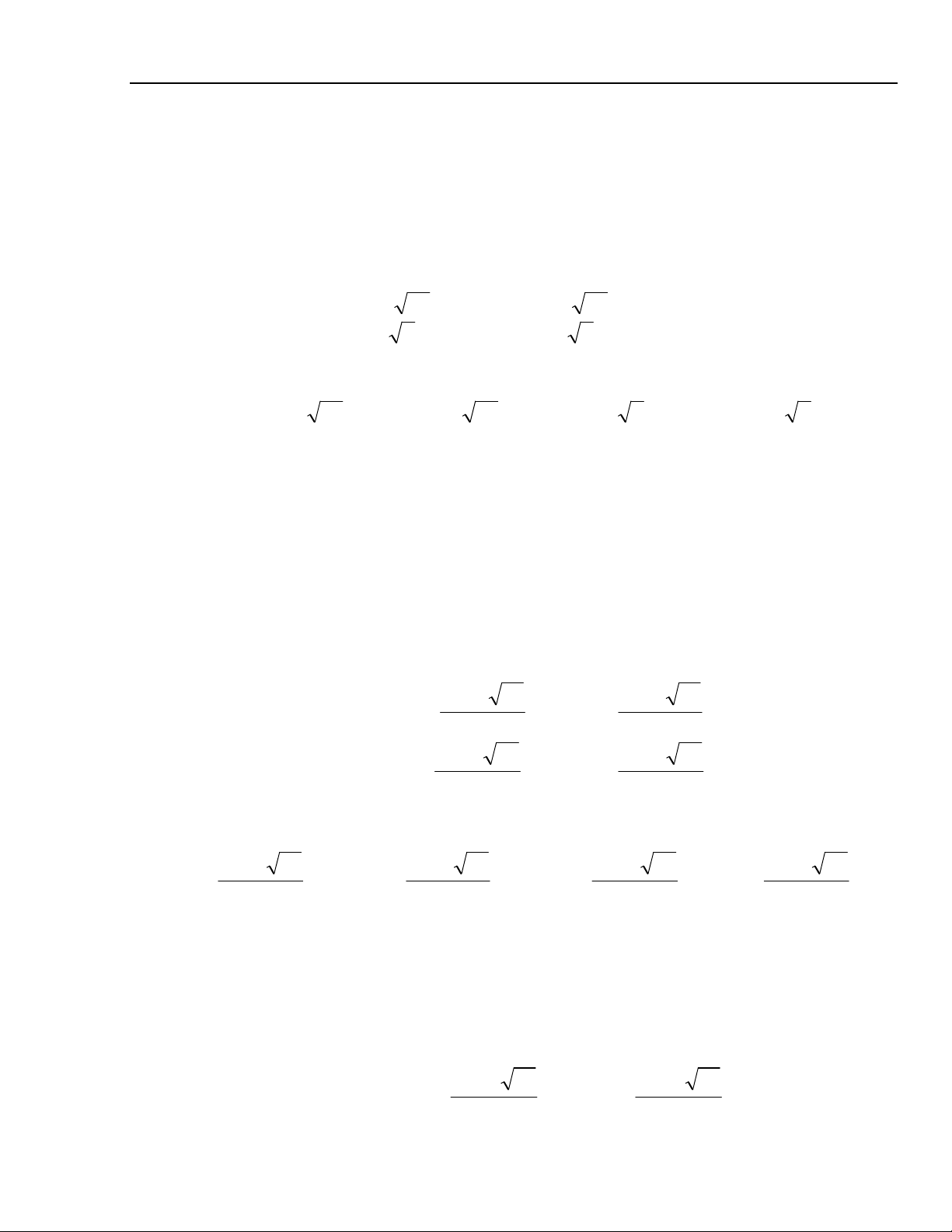
Mt s phng pháp gii phng trình a thc bc cao mt n – V ình Dng
3
Gii
Nhn xét : Ta thy phng trình này không có nghim nguyên
x
4
+ 12x
3
+ 32x
2
- 8x - 4 = 0 ⇔ (x
4
+ 12x
3
+ 36x
2
) - (4x
2
+ 8x + 4) = 0
⇔ (x
2
+ 6x)
2
- (2x + 2)
2
= 0 ⇔ (x
2
+ 8x +2)(x
2
+ 4x -2) = 0
⇔ x
2
+ 8x + 2 = 0 ho%c x
2
+ 4x - 2 = 0
x
2
+ 8x + 2 = 0 ⇔ x =
 +−
ho%c x =
 −−
x
2
+ 4x - 2 = 0 ⇔ x =
+−
ho%c x =
−−
Vy phng trình ã cho có bn nghim
x
1
=
 +−
; x
2
=
 −−
; x
3
=
+−
; x
4
=
−−
II. Phng pháp t n ph
Ví d 3 : Gii phng trình (x
2
+ x + 2)
2
- 12(x
2
+ x + 2) + 35 = 0
Gii
%t x
2
+ x + 2 = y . Ta có phng trình
y
2
- 12y + 35 = 0 ⇔ y = 5 ho%c y = 7
Vi y = 5 ⇔ x
2
+ x - 3 = 0 ⇔ x =
 +−
ho%c x =
 −−
Vi y = 7 ⇔ x
2
+ x -5 = 0 ⇔ x =
 +−
ho%c x =
 −−
Vy phng trình ã cho có bn nghim
x
1
=
 +−
; x
2
=
 −−
; x
3
=
 +−
; x
4
=
 −−
Ví d 4: Gii phng trình (x
2
+ 5x + 4)(x
2
+ 5x + 6) - 3 = 0
Gii
%t x
2
+ 5x + 5 = y. Ta có phng trình
(y - 1)(y + 1) - 3 = 0 ⇔ y
2
= 4 ⇔ y = 2 ho%c y = -2
Vi y = 2 ⇔ x
2
+ 5x + 3 = 0 ⇔ x =
 +−
ho%c x =
 −−
Vi y = -2 ⇔ x
2
+ 5x + 7 = 0 phong trình này vô nghiêm vì ∆ < 0
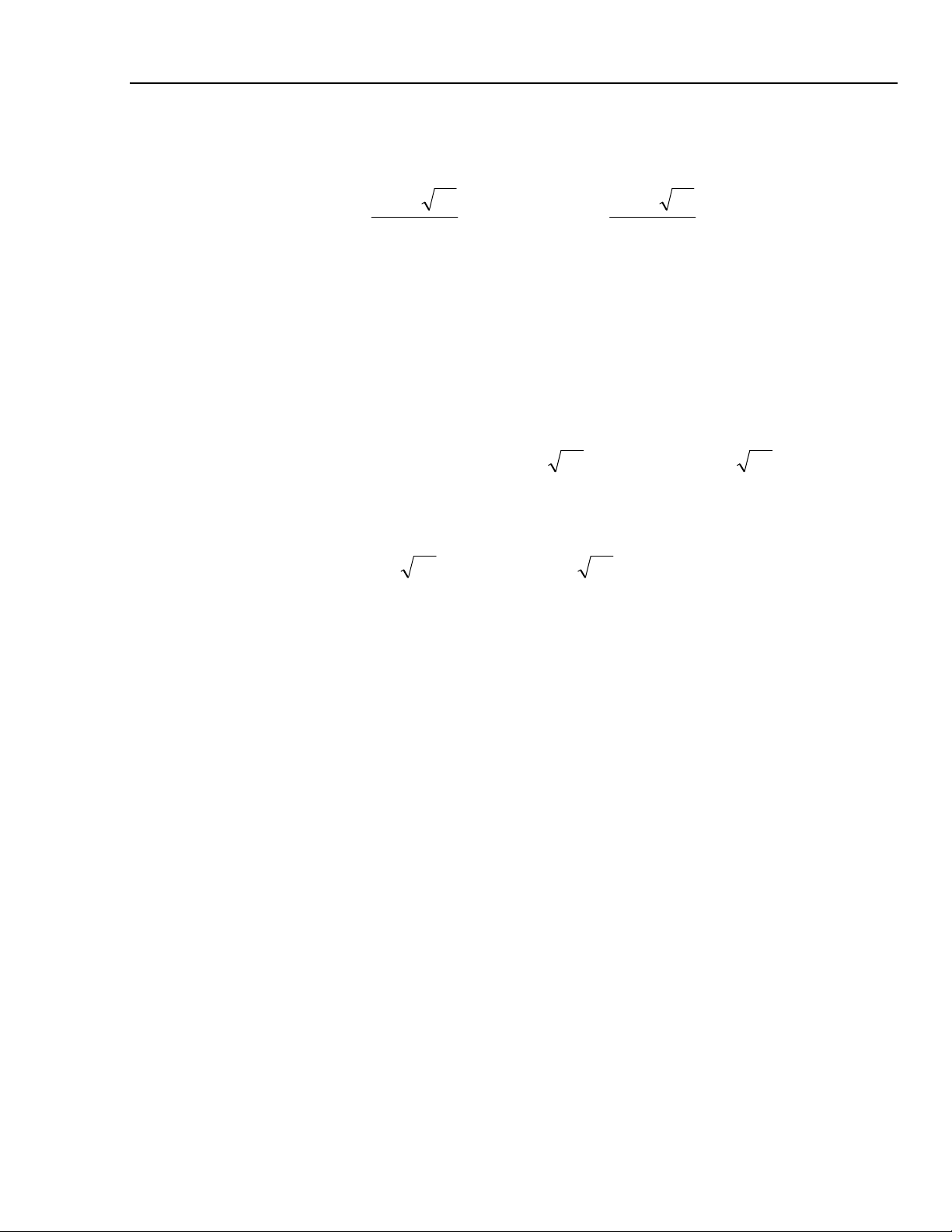
Mt s phng pháp gii phng trình a thc bc cao mt n – V ình Dng
4
Vy phng trình ã cho có hai nghim
x
1
=
 +−
; x
2
=
 −−
Ví d 5 : Gii phng trình (x + 1)(x + 3)(x + 5)(x + 7) = 9
Gii
(x + 1)(x + 3)(x + 5)(x + 7) = 9 ⇔ (x
2
+ 8x + 7)(x
2
+ 8x + 15) - 9 = 0
%t x
2
+ 8x + 11 = y
Ta có phng trình (y - 4)(y + 4) - 9 = 0 ⇔ y
2
= 25 ⇔ y = 5 ho%c y = -5
Vi y = 5 ⇔ x
2
+ 8x + 6 = 0 ⇔ x =
 +−
ho%c x =
 −−
Vi y = -5 ⇔ x
2
+ 8x + 16 = 0 ⇔ (x + 4)
2
= 0 ⇔ x = -4
Vy phng trình ã cho có ba nghim
x
1
=
 +−
; x
2
=
 −−
; x
3
= -4
Bài tp
Bài 1: Gii các phng trình sau:
a) 3x
4
- 22x
2
- 45 = 0 b) x
6
- 9x
3
+ 8 = 0
Bài 2: Gii các phng trình sau:
a) 2x
3
- 11x
2
+ 2x + 15 = 0 b) x
4
+ x
2
+ 6x - 8 = 0 c) x
4
+ 4x
3
+ 3x
2
+ 2x - 1 = 0
Hng dn:
c) x
4
+ 4x
3
+ 3x
2
- 2x - 1 = 0 ⇔ (x
2
+ 2x)
2
- (x - 1)
2
= 0
⇔ (x
2
+ x + 1)(x
2
+ 3x - 1) = 0
Bài 3: Gii các phng trình sau
a) x(x
2
- 1)(x + 2) + 1 = 0 b) (4x + 1)(12x - 1)(3x + 2)(x + 1) = 4
c) (x - 1)(x -2)(x + 4)(x + 5) =112
---------------------------@------------------------
MT S DNG PHNG TRÌNH BC CAO C BIT
I . Phng trình i xng (phơng trình thun nghch)
Mt s phng pháp gii phng trình a thc bc cao mt n – V ình Dng
5
nh ngha:
Phng trình có dng
a
n
x
n
+ a
n - 1
x
n - 1
+ ... + a
1
x + a
0
= 0 ( a ≠ 0).
Trong ó các h s ca các s hng cách u s hng u và s hng cui b!ng nhau (
a
n
= a
0
; a
n-1
= a
1
; ...... ). Gi là phng trình i xng
Nu n là s ch*n ta gi là phng trình i xng bc ch*n, còn n là s l+ ta gi là
phng trình i xng bc l+ .
Ví d: Các phng trình sau là phng trình i xng
a) 2x
4
+ 3x
3
- 16x
2
+ 3x + 2 = 0 (1) ( i xng bc 4)
b) 2x
5
+ 3x
4
- 5x
3
- 5x
2
+ 3x + 2 = 0 ( i xng bc 5)
1. Phng trình i xng bc chn:
a ) Cách gii:
+ Chia c hai v cho
0
2
≠
n
x
+ %t x +
x
1
= y (1)
+ Biu di,n:
+−
+
+=+
−
−
−
−
2
2
1
1
1111
k
k
k
k
k
k
x
x
x
x
x
x
x
x
+ Thay giá tr v"a tìm c ca y tìm giá tr ca x
b) Ví d:
Gii phng trình sau :
2x
4
+ 3x
3
- 16x
2
+ 3x + 2 = 0 (1) ( i xng bc bn)
Gii
Ta thy x = 0 không là nghim ca phng trình . Chia c hai v cho x
2
≠ 0 ta có
phng trình :
2x
2
+ 3x - 16 + 3
x
1
+
2
2
x
= 0
2
++
+x
x
x
x1
3
1
2
2
= 16 = 0
%t x +
x
1
= y (2)
+
2
2
1
x
x
= y
2
- 2 .
Ta có phng trình 2y
2
+ 3y - 20 = 0 có nghim y = -4 , y =
2
5
. Th t- thay y = -4 và
y =
2
5
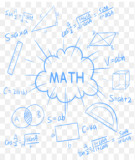
. vào (2) ta có x
1
= -2 +
3
; x
2
= -2 -
3
; x
3
=2 ; x
4
=
2
1