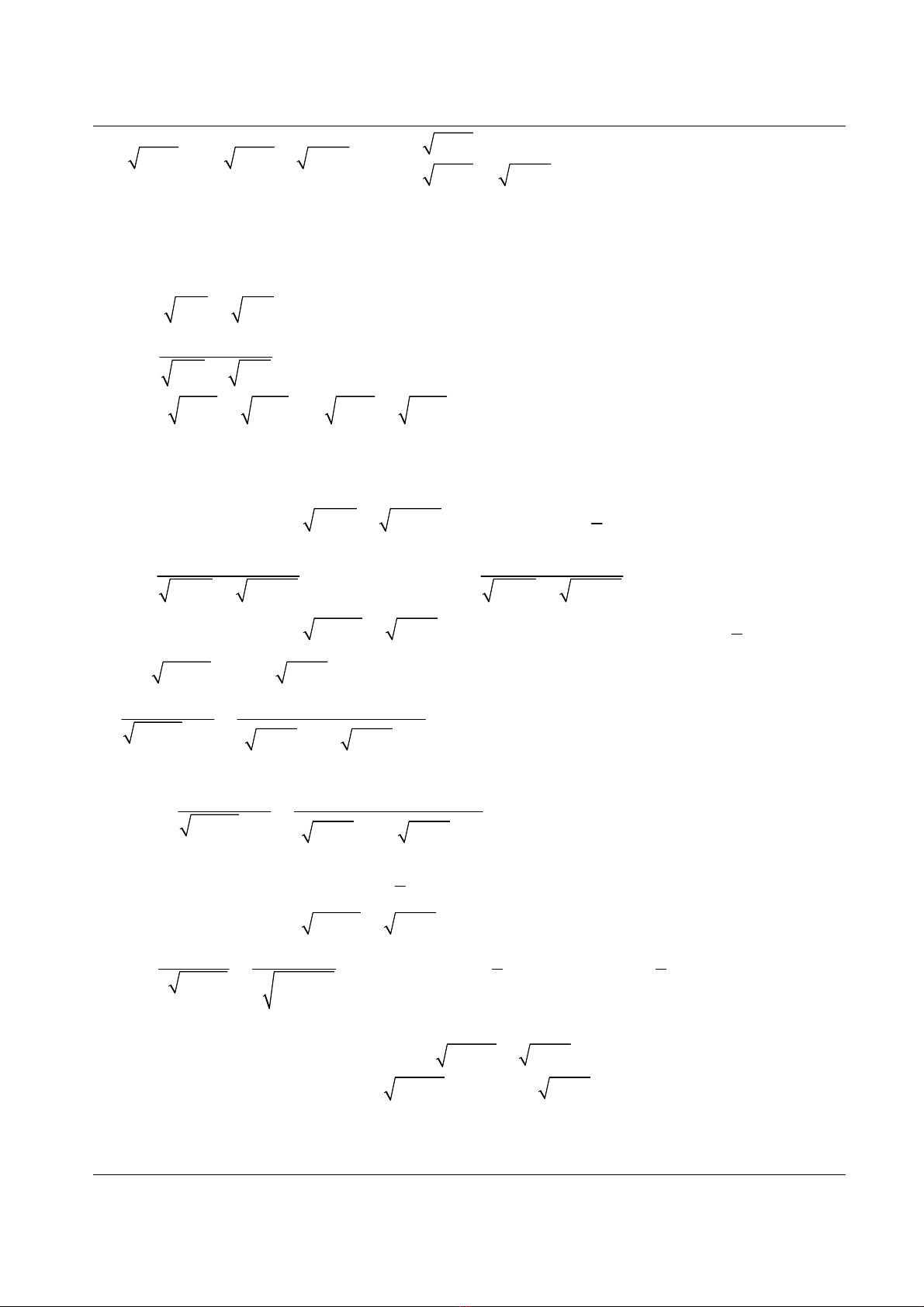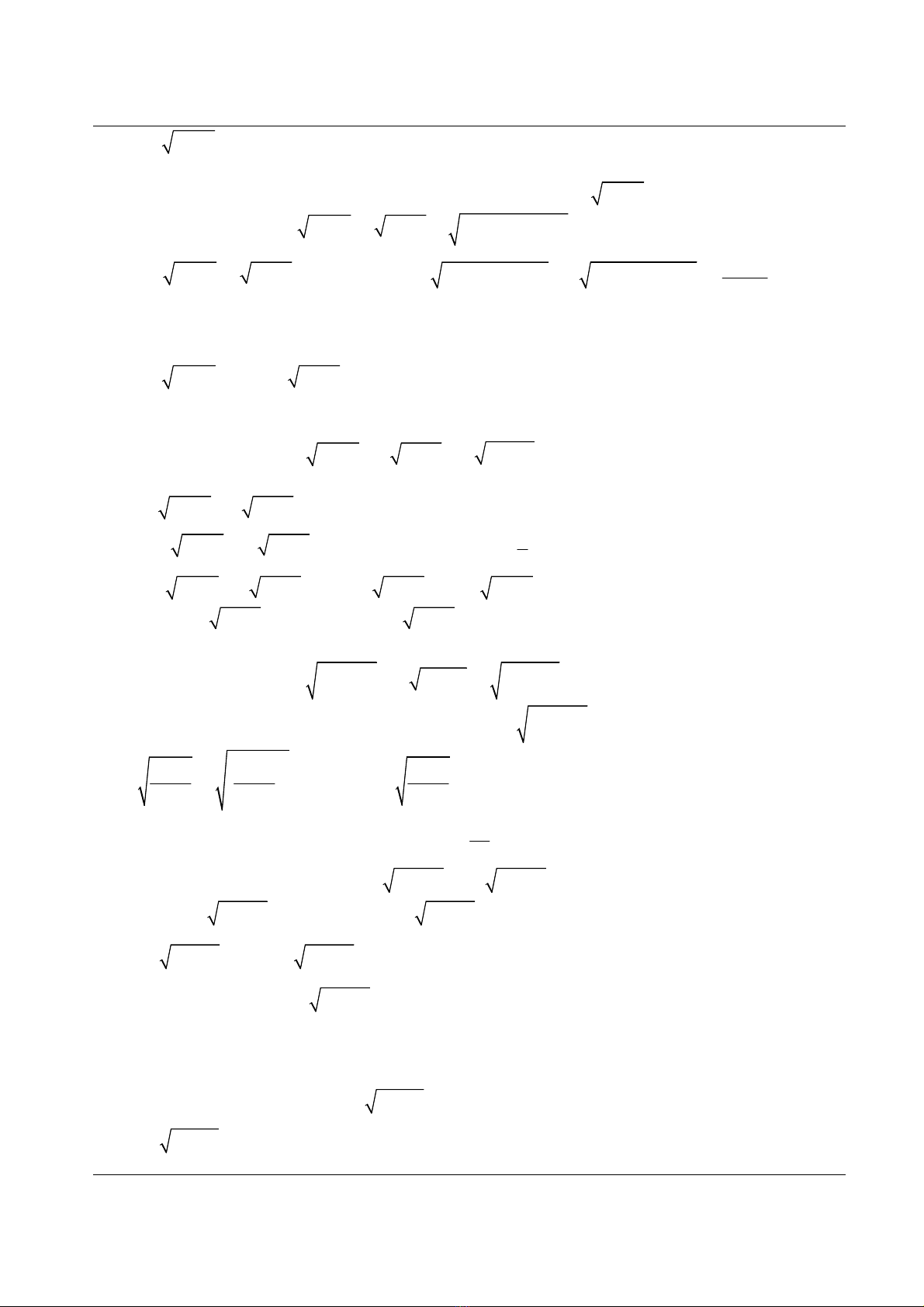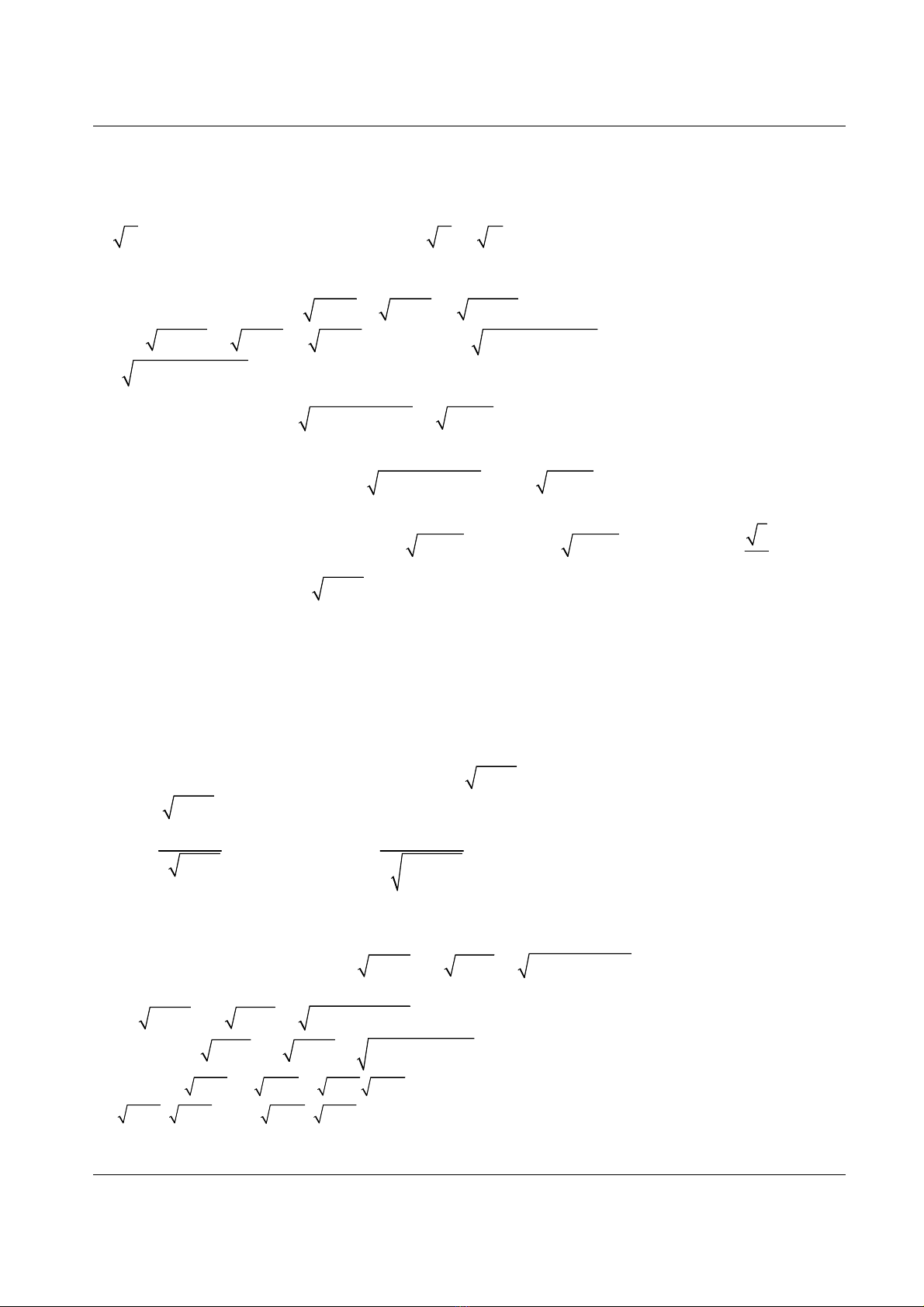
Chuyên đề ôn thi Đại học môn Toán năm 2013 Phương Trình bất phương trình vô tỉ
Ths.Hoàng Huy Sơn 1
PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH VÔ TỈ
A. PHƯƠNG TRÌNH VÔ TỈ
Các dạng cơ bản:
+
2
0
B
A B
A B
+
0,( 0)
A B
A B A B
I. Phương pháp nâng lũy thừa
Ví dụ 1: Giải phương trình:
3 7 2 8.
Điều kiện:
4 7.
x
(1) 2 8 7 3 2 8 2 (2 8)(7 ) 7 3
(2 8)(7 ) 2 5 6.
x x x x x x x x
x x x x
Ví dụ 2: Giải phương trình: 2 2
4 5 1 2.
x x x
Điều kiện:
1 1.
x
Nếu bình phương hai vế của phương trình ta sẽ đưa đến một phương trình bậc cao, do đó chuyển
hạng tử thứ hai sang vế phải ta được:
2 2
4 5 2 1 .
x x x
Với điều kiện
1 1
x
thì
vế phải của phương trình trên không âm nên bình phương hai vế của phương trình ta được phương
trình tương đương: 2 2 2 2 2
4 5 4 4 1 1 1 ( 0).
2
x x x x x x x x
Ví dụ 3: Giải phương trình: 2
3 1 3 8 3(1)
x x x
22
2432
2
2
2
3 8 3 0 3 8 3 0
(1)
9 48 82 57 0
9 1 3 8 3
3 8 3 0 0
3.
3 9 21 19 0
x x x x
x x x x
x x x
x x x
x
x x x x
Chú ý: Có thể giải cách khác (Phương pháp sử dụng tính chất của hàm số đơn điệu) như sau: Điều
kiện:
1.
x
Phương trình (1) tương đương với 2
3 1 3 8 3 0.
x x x
Xét hàm số
2
( ) 3 1 3 8 3, 1.
f x x x x x
3
3 3
( ) 6 8; ( ) 6 0, 1.
2 1 4 1
f x x f x x
xx
Suy ra hàm số lồi trên
[ 1; ).

Vậy, phương trình (1) nếu có nghiệm sẽ có không quá hai nghiệm.
Ta có
(0) (3) 0,
f f
do đó phương trình đã cho có hai nghiệm là
0; 3.
x x
Ví dụ 4: Giải phương trình: 2
2 7 2 1 8 7 1.
x x x x x
Điều kiện:
1 7.
x
Ta có
2
2 7 2 1 8 7 1
( 1) 2 1 2 7 1 7 0
x x x x x
x x x x x
( 1) 2 1 2 7 1 7 0
1 1 2 7 1 2 0
x x x x x
x x x x
Chuyên đề ôn thi Đại học môn Toán năm 2013 Phương Trình bất phương trình vô tỉ
Ths.Hoàng Huy Sơn 2
1 2 1 7 0
x x x
1 2 5
4.
1 7
x x
x
x x
So với điều kiện, ta có nghiệm của phương trình là
4, 5.
x x
Chú ý: Để đưa phương trình đã cho về phương trình tích, ta phải phân tích vế trái của phương trình
( ) 0
f x
thành nhân tử. Một số trường hợp cần đến phép biến đổi nhân lượng liên hợp. Phép biến đổi
nhân lượng liên hợp có hai dạng sau:
Dạng 1.
( ) ( ) ( ) (1),
u x v x f x trong đó
( ) ( )
u x v x
và
( )
f x
có chung nghiệm
0
.
x
Biến đổi (1)
về dạng
( ) ( )
( )
( ) ( )
u x v x
f x
u x v x
sau đó đưa về phương trình tích, trong đó có nhân tử
0
( ).
x x
Dạng 2.
1 1 2 2
( ) ( ) ( ) ( ) ( ) (2),
n n m n
u x v x u x v x f x trong đó
1 1 2 2
( ) ( ) , ( ) ( )
u x v x u x v x
và
( )
f x
có chung nghiệm
0
.
x
Nhân lượng liên hợp từng cụm và sau
đó đưa về phương trình tích, trong đó có nhân tử
0
( ).
x x
Ta xét các ví dụ sau:
Ví dụ 5: Giải phương trình:
4 2 3 1 (1).
x x x
3
.
2
x
1 1
(1) 1 0 (1 ) 1 0 1.
4 2 3 4 2 3
xx x x
x x x x
Ví dụ 6: Giải phương trình: 32
5 1 9 2 3 5 0(1).
x x x x
Điều kiện
1
.
5
x
32
2
3 3
(1) 5 1 2 9 2 2 3 5 0
5( 1) 1
( 1)(2 5) 0
5 1 2 9 2 9 4
x x x x
x x x x
xx x
2
3 3
5 1
( 1) 2 5 0 1.
5 1 2 9 2 9 4
x x x
xx x
(Do biểu thức trong
dấu ngoặc vuông lớn hơn 0 với mọi
1
).
5
x
Cách khác: Hàm số
f x x x x x
32
( ) 5 1 9 2 3 5
có đạo hàm
f x x x
xx2
3
5 1 1
( ) 4 3 0,
5
2 5 1 3 9
nên tăng trên D1
; .
5

Thử được
x
1
là nghiệm nên là nghiệm duy nhất của phương trình đã cho.
Ví dụ 7: (Khối
2010)
B
Giải phương trình: 2
3 1 6 3 14 8 0.
x x x x
Biến đổi phương trình đã cho về dạng:
2
3 1 4 1 6 3 14 5 0.
x x x x
Sau đó nhân lượng liên hợp của các biểu thức trong dấu ngoặc ta được
Chuyên đề ôn thi Đại học môn Toán năm 2013 Phương Trình bất phương trình vô tỉ
Ths.Hoàng Huy Sơn 3
3( 5) 5
( 5)(3 1) 0
3 1 4 1 6
3 1
( 5) 3 1 0 5.
3 1 4 1 6
x x
x x
x x
x x x
x x
Chú ý: Để phân tích được thành nhân tử thuận lợi hơn, ta đưa vào hai ẩn phụ
, .
u v
Ví dụ 8: Giải phương trình: 2 2
2 1 2 ( 1) 2 3 0
x x x x x x
(1)
Đặt:
2 2
2 2 2
2 2
2 2
2
2 1
2, 0 2
1
2 3
2 3, 0
2
v u x
u x u u x
v u
v x x x
v x x v
(1) trở thành
0 ( )
1
( ) ( ) 1 0 1
( ) 1 0 ( )
2 2 2 2
v u a
v u
v u v u v u
v u b
Vì
0, 0
u v
nên
( )
b
vô nghiệm.
Do đó
( )
a
2 2
1
0 2 3 2 .
2
v u v u x x x x
Ví dụ 9: Giải phương trình: 2 2
6 10 5 (4 1) 6 6 5 0(1)
x x x x x
2 2
(1) 6 6 5 (4 1) (4 1) 6 6 5 1 0.
x x x x x x
Đặt 2
6 6 5 0,
u x x
4 1.
v x
Ta có phương trình 2
1 0
u v vu
( 1)( 1) (1 ) 0 ( 1)( 1 ) 0 1 0.
u u v u u u v u v
Vậy ta có
2
2
0
3 59
6 6 5 4 .
10 6 5 0 10
x
x x x x
x x
Ví dụ 10: Giải phương trình: 2 2
8 8 3 8 2 3 1.
x x x x x
(1)
2 2
2 2
(1) 4(2 3 1) 4 1 8 2 3 1
4 1 2 ( 2 3 1; 4 )
x x x x x x
u v uv u x x v x
2
(4 1) (2 1) 0 (2 1)(2 1) 0
u v u u u v
2 2
3 3
2 1 0 2 2 3 1 1 8 12 3 0 .
4
u x x x x x
2 1 0
u v
2
2
1
1 7
2 2 3 1 4 1 .
44
8 4 3 0
x
x x x x
x x
II. Phương pháp đặt ẩn phụ.
1) Dạng 1. Sử dụng một ẩn phụ để chuyển phương trình ban đầu về phương trình với một ẩn phụ.
Ví dụ 1: Giải phương trình:
2
5 2 3 3
x x x x
(1)
Phương trình (1) được biến đổi về dạng: 2 2
3 3 3 10 0.
x x x x
Đặt 2
3 0.
t x x
Phương trình trở thành 2
3 10 0.
t t
Chọn
2.
t
Từ đó tìm được
1, 4.
x x
Ví dụ 2: Giải phương trình:
2 3 2 1 0.
x x x x
Chuyên đề ôn thi Đại học môn Toán năm 2013 Phương Trình bất phương trình vô tỉ
Ths.Hoàng Huy Sơn 4
Đặt 2 2
2 0 2 2.
u x u x x u
Ta có phương trình
2 2 3 2
( 2) 3 3 0 3 0 1 2 1 1.
u u u u u u u u x x
Ví dụ 3: Giải phương trình:
3 6 3 6 3
x x x x
(1)
Đặt: 2
3 6 0 9 2 (3 )(6 )
t x x t x x
2
9
(3 )(6 )
2
t
x x
(1) trở thành phương trình: 2
2 3 0.
t t
Phương trình đã cho có nghiệm là
3,
x
6.
x
Chú ý: Cũng có thể đưa về 2 biến phụ như ở dạng 3 sau đây:
Đặt
3 0, 6 0.
u x v x
Ta có hệ phương trình theo
u
và
:
v
2 2
3
9
u v uv
u v
. Giải hệ
tìm
,
u v
từ đó tìm
.
x
Ví dụ 4: Giải phương trình: 2
3 2 6 2 4 4 10 3 .
x x x x
Điều kiện
2 2.
x
Đặt
2 2 2 .
t x x
(1) trở thành 2
3 0 3.
t t t t
0
t
2 2 2 2 8 4
x x x x
6
5
x
3 2 2 2 3 2 2 3 2
8 4 12 2 9 2 12 2 5 15(*)
t x x x x
x x x x x
Do
2 2
x
nên vế trái của (*) âm. Suy ra phương trình (*) vô nghiệm.
Ví dụ 5: Giải phương trình:
2 2
52
5 5
2 1 3 1 1 0
x x x
(1)
Vì
1
x
không là nghiệm, nên chia hai vế của (1) cho
2
5
1
x ta được phương trình
2
5 5
1 1
2 3 0.
1 1
x x
x x
Đặt 51
.
1
x
t
x
Ta được: 2
3 2 0 1 2.
t t t t
Giải phương trình ta được nghiệm đã cho là
33
.
31
x
Ví dụ 6: Giải phương trình: 2 2 2
2 3 2 3 9.
x x x x x
(1)
2 2 2 2
2
2 2
(1) 2 3 3 3 12
3 3 12 0
x x x x x x
x x x x
2 2
12 0 ( 3) 4 3.
t t t x x t t
Từ đó
1.
x
2) Dạng 2. Sử dụng một ẩn phụ để chuyển phương trình ban đầu về phương trình với một ẩn phụ
nhưng các hệ số vẫn còn chứa ẩn
.
x
Khi đó ta đưa về phương trình bậc hai theo ẩn mới hoặc ẩn
x
nhưng có biệt số
là một chính phương.
Ví dụ 7: Giải phương trình:
2 2
4 1 1 2 2 1 1
x x x x
Đặt
2 2 2 2
1 1 1 1 4 1 2 2 1
t x t x x t t x
Chuyên đề ôn thi Đại học môn Toán năm 2013 Phương Trình bất phương trình vô tỉ
Ths.Hoàng Huy Sơn 5
2
1
2 4 1 2 1 0
2
t x t x t
(loại) 2
2 1 1 2 1
t x x x
Giải phương trình ta được
4
.
3
x
Chú ý: Có thể bình phương hai vế của phương trình để khử căn, nhưng phải có điều kiện:
1
.
4
x
Ví dụ 8: Giải phương trình: 2 2
1 2 2 .
x x x x
Đặt 2
2 0.
t x x
Phương trình trở thành
2
2 2 2
2 1 0, 1 2 1 1 .
x tx t x x x
Từ đó ta có
2
1 2 1 .
x t x x x x Giải phương trình ta được
1 5.
x
3) Dạng 3. Sử dụng
2
(hoặc
)
k
ẩn phụ để chuyển phương trình ban đầu về hệ phương trình với
2
(hoặc
)
k
ẩn phụ. Chẳng hạn đối với phương trình:
( ) ( ) .
m n
a f x b f x c
Ta có thể đặt
( ); ( ).
m n
u a f x v b f x
Suy ra
.
m n
u v a b
Ta thu được hệ
m n
u v a b
u v c
Ví dụ 9: Giải phương trình:
2
1 1 1
x x x x x x
Đặt
1; 1 0.
u x v x
Suy ra 2 2
1.
u v
Ta thu được hệ
2 2
2 2
1 (1)
1 (2)
u v
u v uv uv
.
Thay phương trình (1) vào (2) ta được
2 2 2 2 2 2
0 1 1 0.
u v uv uv u v v v uv uv v v u
+ Trường hợp
0
v
ta được
1.
x
+ Trường hợp
1
v
ta được
2.
x
+ Trường hợp
1
u
ta được
1.
x
Chú ý: Có thể giải cách khác bằng cách biến đổi đưa về phương trình tích.
Ví dụ 10: Giải phương trình: 2
(13 4 ) 2 3 (4 3) 5 2 2 8 16 4 15
x x x x x x
(1)
Đặt 2 2 2 2
2 3 0, 5 2 0 2 3, 5 2 2.
u x v x u x v x u v
2 2
2 2
2 2
3 3
2
(1) 7 2 7 2 2 8
2 1
2.
1
7( ) 2( ) 8 2
u v
u u v v uv
u v u x
v
u v u v uv
III. Phương pháp sử dụng tính chất của hàm số đơn điệu.
Sử dụng tính chất đơn điệu của hàm số để giải phương trình là cách giải khá quen thuộc. Ta có ba
hướng áp dụng như sau.
1. Biến đổi phương trình về dạng:
( )
f x k
(1), với
k
là hằng số.
Nếu hàm số
f
đồng biến (nghịch biến) trên khoảng
( ; )
a b
thì phương trình (1) có nhiều nhất
một nghiệm trên khoảng
( ; ).
a b
Do đó nếu tìm được
0
x
thuộc khoảng
( ; )
a b
sao cho
0
( )
f x k
thì
0
x
là nghiệm duy nhất của phương trình.
2. Biến đổi phương trình về dạng:
( ) ( ) (2)
f x g x