4.2. Chän vµ x¸c ®Þnh th«ng sè bé ®iÒu chØnh.
4.2.1. Chän bé ®iÒu chØnh.
Mçi mét hÖ thèng ®iÒu khiÓn tù ®éng ®Òu cÇn ph¶i æn ®Þnh vµ chÝnh x¸c.
§Ó hÖ thèng æn ®Þnh chóng ta ph¶i tæng hîp hÖ thèng. ViÖc tæng hîp hÖ thèng
cã thÓ thùc hiÖn b»ng nhiÒu ph−¬ng ph¸p nh− lµ thay ®æi th«ng sè cña hÖ
thèng hoÆc thay ®æi cÊu tróc cña hÖ thèng b»ng c¸ch l¾p thªm vµo ®ã c¸c bé
®iÒu chØnh. Cã nh÷ng hÖ thèng ®iÒu khiÓn dï thay ®æi th«ng sè ®Õn møc nµo
còng kh«ng lµm nã æn ®Þnh ®−îc. V× vËy ta nªn sö dông ph−¬ng ph¸p thay ®æi
cÊu tróc cña hÖ thèng. Sau ®©y lµ mét sè bé ®iÒu chØnh ®iÓn h×nh ®ã:
* Bé ®iÒu chØnh tû lÖ (P).
* Bé ®iÒu chØnh tÝch ph©n (I).
* Bé ®iÒu chØnh tû lÖ tÝch ph©n (PI).
* Bé ®iÒu chØnh vi ph©n (D).
* Bé ®iÒu chØnh tû lÖ vi ph©n (PD).
* Bé ®iÒu chØnh tû lÖ vi tÝch ph©n (PID).
Tr−íc khi chän bé ®iÒu chØnh ta cÇn hiÓu kh¸i niÖm sai lÖch tÜnh lµ g×. Sai
lÖch tÜnh x¸c ®Þnh ®é chÝnh x¸c tÜnh cña hÖ. Sai lÖch tÜnh ®−îc tÝnh theo ®Þnh
lý tíi h¹n:
()
== ∞>− tee t
ss lim
0
)(.lim
>−s
sEs
H×nh 4.4 cã nªu ¶nh h−ëng cña c¸c bé ®iÒu chØnh kh¸c nhau ®èi víi sai lÖch
e(t) cña hÖ:
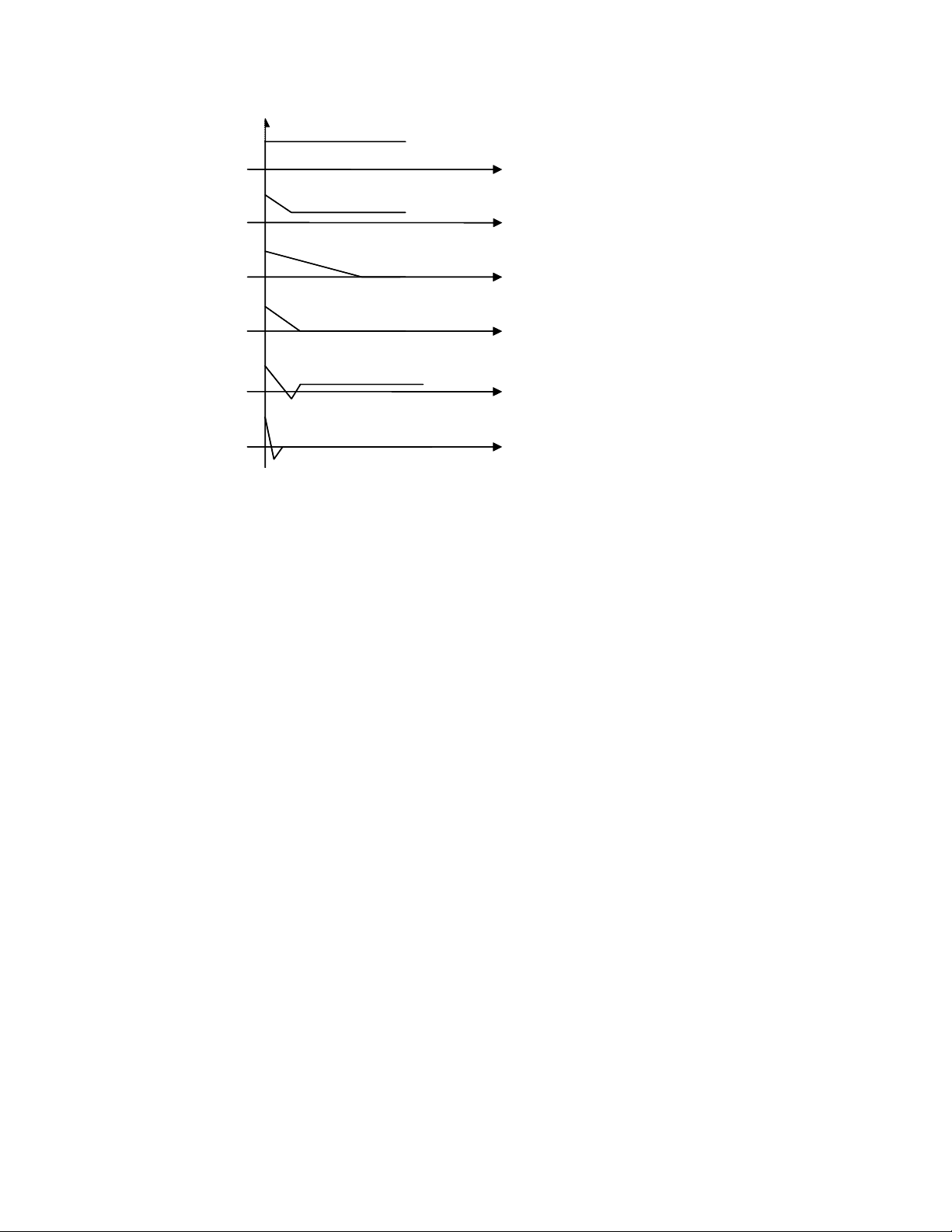
H×nh 4.4 - ¶nh h−ëng cña c¸c bé ®iÒu chØnh ®èi víi sai lÖch e(t)
a) Kh«ng cã bé ®iÒu chØnh.
b) Bé ®iÒu chØnh tû lÖ P.
c) Bé ®iÒu chØnh tÝch ph©n I.
d) Bé ®iÒu chØnh tû lÖ tÝch ph©n PI.
e) Bé ®iÒu chØnh tû lÖ vi ph©n PD.
f) Bé ®iÒu chØnh tû lÖ vi tÝch ph©n PID.
Trong c¸c bé ®iÒu chØnh trªn th× bé ®iÒu chØnh tû lÖ lµ ®¬n gi¶n nhÊt, t¸c
®éng nhanh nh−ng nã kh«ng triÖt tiªu ®−îc sai lÖch tÜnh v× hÖ sè khuÕch ®¹i
cao qu¸ sÏ lµm hÖ thèng mÊt æn ®Þnh.
Víi bé ®iÒu chØnh I th× nã cã thÓ triÖt tiªu ®−îc sai lÖch tÜnh. Nh−ng tÝn
hiÖu ®iÒu khiÓn chËm so víi sai lÖch 900 nªn hÖ thèng mÊt æn ®Þnh. V× vËy mµ
®iÒu chØnh I vµ P kh«ng ®−îc sö dông réng r·i mµ ph¶i kÕt hîp P vµ I thµnh bé
®iÒu chØnh PI.
§èi víi bé ®iÒu chØnh vi ph©n th× còng gièng nh− bé P lµ sÏ cã sai lÖch
tÜnh vµ hÖ thèng sÏ mÊt æn ®Þnh khi cã nhiÔu t¸c ®éng nªn ta còng kh«ng sö
dông bé ®iÒu chØnh D ®¬n thuÇn mµ th−êng kÕt hîp víi bé ®iÒu khiÓn P =>
PD vµ PI =>PID. Thµnh phÇn vi ph©n D lµm t¨ng nhanh tèc ®é t¸c ®éng do
a)
b)
c)
d)
e)
f
)
t
t
t
t
t
t
e(t)
kh©u vi ph©n cho ®Çu ra sím pha so víi ®Çu vµo gãc Π/2. Tuy nhiªn quy luËt
PD kh«ng lµm gi¶m sai lÖch tÜnh. V× vËy trong c«ng nghiÖp th−êng sö dông
trong hÖ thèng ®ßi hái t¸c ®éng nhanh. Bé ®iÒu chØnh PID lµ bé ®iÒu chØnh kÕt
hîp ®−îc −u ®iÓm cña c¶ 3 bé ®iÒu chØnh P,I,D. Tuy nhiªn bé ®iÒu chØnh nµy
sÏ rÊt phøc t¹p nªn ng−êi ta th−êng hay sö dông bé ®iÒu khiÓn PD,PI.
Thùc tÕ bé ®iÒu khiÓn PD ®−îc dïng trong ®iÒu khiÓn ng−êi m¸y, tay
m¸y; cßn PI ®−îc dïng trong ®iÒu khiÓn qu¸ tr×nh nh− nhiÖt ®é, ¸p suÊt lùc.
V× vËy trong ®Ò tµi nµy chóng t«i chän bé ®iÒu chØnh PI.
4.2.2. X¸c ®Þnh th«ng sè bé ®iÒu chØnh.
Hµm truyÒn cña bé ®iÒu chØnh PI lµ: GPI(s) = Kp
T
T
i
i
s
s
.
.1+
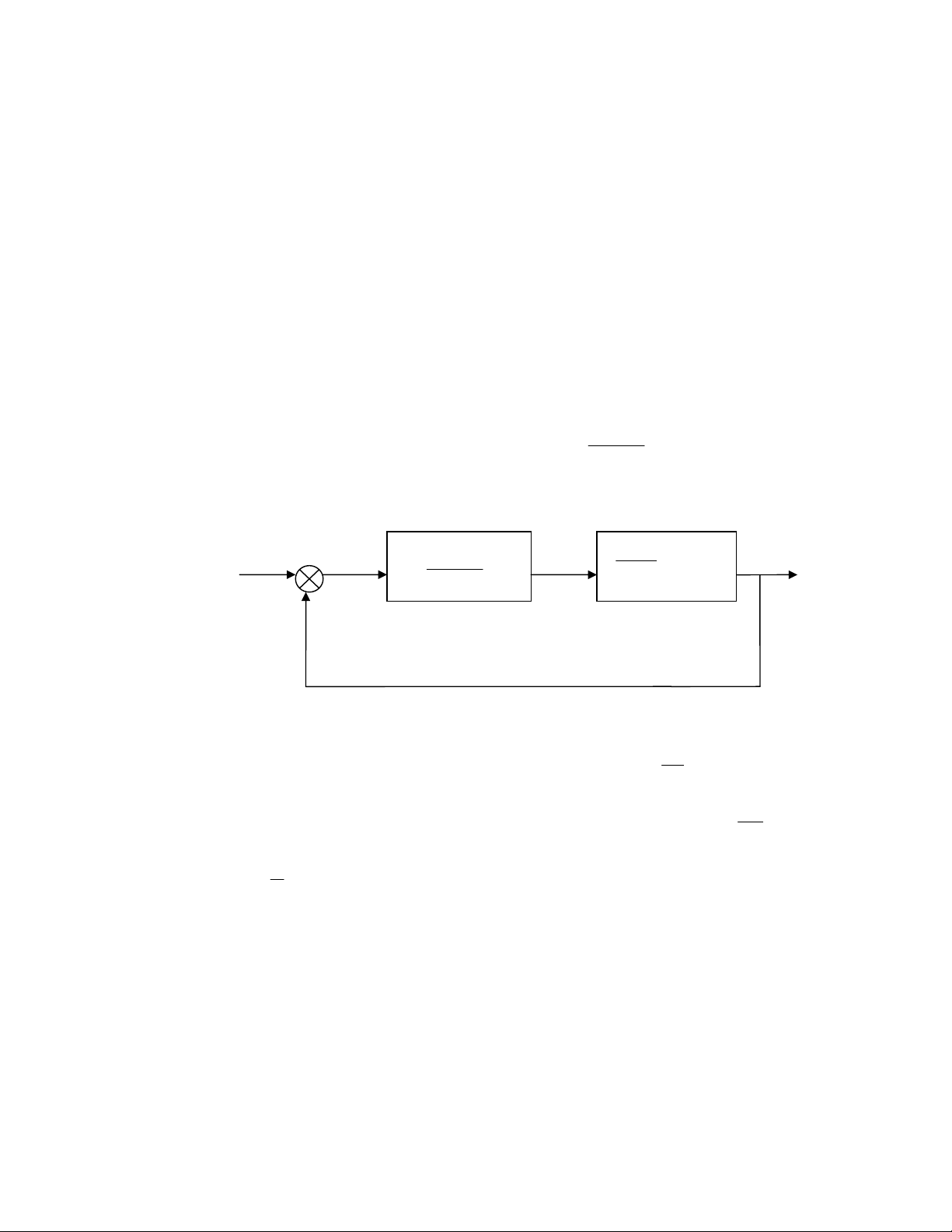
S¬ ®å hÖ thèng ®iÒu khiÓn ®−îc vÏ l¹i nh− sau:
Th«ng th−êng th«ng sè tèi −u ®−îc chän lµ: Ti = T = 36
Hµm truyÒn cña hÖ hë ®−îc chän lµ: W(s) = Gc(s)*G(s) = es
Ts
K
τ
−
1víi K1= Kp.K
M«®un vµ pha ®−îc x¸c ®Þnh nh− ë h×nh IV.2.2 vµ b»ng: |W(jω)| = T
K
ω
1
ϕ = -ω
τ
- 2
π
Z
Y
U X E es
Ts
K
τ
−
+
1
Kp
T
T
i
i
s
s
.
.1+
H×nh 4.5 - §Æc tÝnh tÇn biªn pha cña hÖ thèng.
NÕu ®é dù tr÷ æn ®Þnh vÒ biªn ®é ®−îc chän lµ 0,5 ( ®é dù tr÷ æn ®Þnh vÒ biªn
®é x¸c ®Þnh bëi tû sè cña hÖ sè khuÕch ®¹i giíi h¹n kg víi hÖ sè khuÕch ®¹i
hiÖn hµnh: β =
()
||
1
π
ω
jWk
kg=); øng víi gãc lÖch pha -
π
= -
ω
π
τ - 2
π
Tõ ®ã : : |W(j
ω
π
)| =
τ
π
T
K
.
2
1
Víi ®é dù tr÷ æn ®Þnh nh− trªn ta cã: K1= Kp.K ≤ 4
π
τ
T= 4
π
= 35,34
Ö
Kp ≤ 35,34: 3,9 = 9
VËy bé ®iÒu chØnh PI ®−îc chän nh− sau: GPI(s) = 9.
s
s
36
361+
§Ó thùc hiÖn hµm nµy trong vi ®iÒu khiÓn ta ph¶i tiÕn hµnh chuyÓn nã vÒ
ph−¬ng tr×nh sai ph©n b»ng c¸ch thay 1
1
.
2
+
−
=z
z
T
svíi T lµ thêi gian trÝch mÉu
(LÊy thêi gian trÝch mÉu lµ 1s) ta cã: G(z) = 1
7172
−
−
z
z hay =
)(
)(
zU
zY
1
7172
−
−
z
z
Ù Y(z).z - Y(z) = 72.U(z).z - 71U(z).
Ù Y(z).z = 72.U(z).z - 71.U(z) + Y(z)
Víi Y(z) lµ tÝn hiÖu ra rêi r¹c vµ U(z) lµ tÝn hiÖu vµo rêi r¹c.
Theo tÝnh chÊt dÞch hµm gèc th× zz.Y(z) = Y(k+n)
Nh− vËy ta cã Y(k+1) = 72.U(k+1) - 71.U(k)+Y(k)
Ch¦¥ng V