Sáng kiến kinh nghiệm dự thi cấp tỉnh Trang 1
1. Tên sáng kiến:
“ HƯỚNG DẪN SỬ DỤNG PHẦN MỀM ZIPGRADE CHẤM TRẮC NGHIỆM
BẰNG ĐIỆN THOẠI SMARTPHONE VÀ ỨNG DỤNG MÁY TÍNH CẦM TAY VÀO
LÀM NHANH BÀI TẬP TOÁN TRẮC NGHIỆM THI THPT QUỐC GIA”
2. Lĩnh vực áp dụng sáng kiến: CÁC MÔN THI TRẮC NGHIỆM VÀ MÔN T O Á N 1 2
3. Thời gian áp dụng sáng kiến:
Từ ngày 05 tháng 09 năm 2016 đến ngày 26 tháng 05 năm 2017
Sáng kiến kinh nghiệm dự thi cấp tỉnh Trang 2
I. ĐIỀU KIỆN HOÀN CẢNH TẠO RA SÁNG KIẾN
Kì thi THPT quốc gia 2017, các bài Toán, Ngoại ngữ, Khoa học Tự nhiên và Khoa học
Xã hội thi theo hình thức trắc nghiệm khách quan; thí sinh làm bài thi trên phiếu trả lời trắc
nghiệm; nội dung thi trong chương trình lớp 12 THPT. Để đáp ứng tốt với những thay đổi này,
việc giảng dạy của giáo viên và học tập học sinh cần được điều chỉnh một cách kịp thời và phù
hợp nhất.
Ở mỗi tiết dạy, song song với việc tổ chức học tập như trước đây thì việc rèn luyện các
dạng bài tập trắc nghiệm ứng với từng đơn vị kiến thức của từng bài, từng chương, từng chủ đề
cần được quan tâm tối đa. Đi cùng với đó là cách kiểm tra đánh giá thông qua đề trắc nghiệm
hoặc trắc nghiệm kết hợp với tự luận cũng phải thay đổi sao cho hợp với kì thi THPT Quốc
Gia.
Vấn đề đặt ra:
+ Một là, đối với giáo viên một đề kiểm tra trắc nghiệm với nhiều mã đề khác nhau cần
chấm như thế nào để giảm thời gian chấm trả bài cho học sinh, hạn chế sai sót là điều rất quan
trọng. Nhằm giúp các thầy cô và nhà trường chưa có máy chấm trắc nghiệm, trong sáng kiến
này chúng tôi muốn dành một phần để chia sẻ việc áp dụng phần mềm ZipGrade trên điện
thoại smartphone giải quyết vấn đề này. Qua đó kiểm tra được đúng năng lực học sinh từ đó
thay đổi phương pháp để giảng dạy có hiệu quả hơn.
+ Hai là, đối với học sinh trong một khoảng thời gian ngắn nhất với lượng kiến thức
được trang bị theo chương trình, học sinh phải chọn được một phương án thoả mãn yêu cầu đề
bài. Ngoài việc nắm vững kiến thức, biết suy luận lôgíc, biết các kỹ thuật làm bài trắc nghiệm
khách quan ... đôi khi học sinh phải thực hiện nhiều phép toán dài phức tạp. Một công cụ hữu
hiệu góp phần hỗ trợ học sinh giải quyết vấn đề này là: Máy tính cầm tay. Mặt khác, khi biết
sử dụng thành thạo máy tính cầm tay để giải toán, học sinh còn tự rèn luyện khả năng tư duy
thuật toán, qua đó giúp các em củng cố khắc sâu kiến thức hơn, nâng cao khả năng tư duy
lôgíc, giúp các em học tốt hơn.
Chính vì thế chúng tôi đã chọn đề tài sáng kiến: HƯỚNG DẪN SỬ DUNG PHẦN
MỀM ZIPGRADE CHẤM TRẮC NGHIỆM BẰNG ĐIỆN THOẠI SMARTPHONE
VÀ ỨNG DỤNG MÁY TÍNH CẦM TAY VÀO LÀM NHANH BÀI TẬP TOÁN TRẮC
NGHIỆM THI THPT QUỐC GIA.
II. MÔ TẢ GIẢI PHÁP
1. Mô tả giải pháp trước khi tạo ra sáng kiến
Ngày nay công nghệ thông tin càng ngày được áp dụng nhiều vào giáo dục, việc chấm
điểm lên điểm sao cho nhanh và chuẩn xác cũng rất quan trọng, giúp nhà trường và giáo viên
giảm được rất nhiều thời gian và công sức trong việc đánh giá học sinh, phù hợp với hình thức
Sáng kiến kinh nghiệm dự thi cấp tỉnh Trang 3
thi trắc nghiệm như hiện nay. Chính vì thế việc sử dụng phần mềm hỗ trợ một cách thành thục
là rất quan trọng đối với giáo viên.
Những năm trước đây với hình thức thi tự luận, việc trình bày cẩn thận, từng bước,
từng bước một sẽ mang lại kết quả tốt thì ở cách thi trắc nghiệm khách quan, tốc độ và sự
chính xác ở kết quả mới là quan trọng. Để giải những bài tập trắc nghiệm môn Toán một cách
dễ dàng, việc thông thạo kỹ năng sử dụng máy tính cầm tay là điều cực kỳ cần thiết. Nó giúp
học sinh dễ dàng kiểm tra được đáp án chính xác.
Việc dạy và học toán có sự hỗ trợ của máy tính đã trở nên rất phổ biến trên toàn thế giới.
Trong các tài liệu giáo khoa của các nước có nền giáo dục tiên tiến luôn có thêm mục sử dụng
máy tính để giải toán.
Trong nhiều năm qua Bộ giáo dục và đào tạo đã có chủ trương đưa máy tính Casio và
Vinacal vào giảng dạy trong trường THPT. Hàng năm có tổ chức các cuộc thi giải toán trên
máy tính Casio và Vinacal từ cấp tỉnh đến cấp quốc gia, tuy nhiên việc hướng dẫn cho học sinh
vận dụng các loại máy tính cầm tay một cách sáng tạo trong quá trình học tập bộ môn Toán nói
riêng và các môn tự nhiên nói chung vẫn còn hạn chế. Nhìn chung học sinh chỉ sử dụng máy
tính ở mức độ thực hiện các phép tính đơn giản mà chưa ứng dụng máy tính ở mức độ cao hơn
như dự đoán kết quả, tư duy toán học dựa trên công cụ máy tính…
Máy tính cầm tay giúp giáo viên và học sinh bổ sung nhiều kiến thức Toán học cơ bản,
hiện đại và thiết thực. Nhờ khả năng xử lí dữ liệu phức tạp với tốc độ cao, máy tính cầm tay
cho phép thiết kế những bài tập toán gắn với thực tế hơn. Chính vì vậy chúng tôi thấy việc giới
thiệu sử dụng máy tính cầm tay trong chương trình giáo dục phổ thông là một việc cần thiết và
thích hợp trong hoàn cảnh thực tế hiện nay.
Qua quá trình giảng dạy chúng tôi đã tích lũy được một số kinh nghiệm cho nội dung
này. Các vấn đề trình bày trong sáng kiến kinh nghiệm là các chuyên đề đã được ứng dụng
trong giảng dạy và đã được phổ biến đến đồng nghiệp trong các cuộc họp tổ, nhóm chuyên
môn. Bản thân chúng tôi đã nhận được nhiều ý kiến phản hồi, khích lệ từ các đồng nghiệp.
Sáng kiến kinh nghiệm này là sự tổng kết có chọn lọc các chuyên đề của bản thân đã viết ra
trong thực tiễn giảng dạy cùng với sự đóng góp nhiệt tình của đồng nghiệp.
So với đề thi tự luận, đề thi trắc nghiệm có số lượng câu hỏi nhiều hơn nhưng thời
gian làm bài ngắn hơn. Do vậy, việc sử dụng máy tính cầm tay để hỗ trợ cho giải trắc
nghiệm là rất cần thiết. Tuy nhiên, chúng ta không nên quá lạm dụng máy tính cầm tay mà
vẫn phải xác định rõ: kiến thức là trọng tâm, máy tính cầm tay chỉ là công cụ hỗ trợ.
Trong phần hai của sáng kiến kinh nghiệm này quy trình ấn máy chúng tôi chủ yếu thao
tác trên máy tính Casio Fx 570ES plus. Đây là loại máy tính thông dụng đối với học sinh hiện
nay.
2. Mô tả giải pháp sau khi có sáng kiến
Báo cáo sáng kiến kinh nghiệm này gồm 2 phần
Phần 1.HƯỚNG DẪN SỬ DỤNG PHẦN MỀM ZIPGRADE CHẤM TRẮC NGHIỆM
BẰNG ĐIỆN THOẠI SMARTPHONE
Sáng kiến kinh nghiệm dự thi cấp tỉnh Trang 4
Phần 2. ỨNG DỤNG MÁY TÍNH CẦM TAY VÀO LÀM NHANH BÀI TẬP TOÁN
TRẮC NGHIỆM THI THPT QUỐC GIA
Trong phần 2 gồm có 6 vấn đề
Vấn đề 1. Ứng dụng máy tính cầm tay vào bài toán trắc nghiệm liên quan đến hàm số
1.1 Tính đạo hàm của hàm số tại điểm
1.2 Tiếp tuyến của đồ thị hàm số
1.3 Xét tính đơn điệu của hàm số
1.4 Cực trị của hàm số
1.5 Giới hạn, tiệm cận của đồ thị hàm số
1.6 Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
1.7 Bài toán tương giao giữa hai đồ thị
Vấn đề 2. Ứng dụng máy tính cầm tay vào bài toán trắc nghiệm liên quan đến phương
trình và bất phương trình
2.1 Phương trình
2.2 Bất phương trình
Vấn đề 3. Ứng dụng máy tính cầm tay vào bài toán trắc nghiệm liên quan đến hàm số
mũ, hàm số lũy thừa và hàm số lôgarit
3.1 Tìm số chữ số của một lũy thừa
3.2 Tính nhanh giá trị biểu thức mũ và logarit
3.3 Xét tính đúng sai của mệnh đề mũ và logarit
Vấn đề 4. Ứng dụng máy tính cầm tay vào bài toán trắc nghiệm liên quan đến nguyên
hàm, tích phân và ứng dụng.
Vấn đề 5: Ứng dụng máy tính cầm tay vào bài toán trắc nghiệm liên quan đến tọa độ
trong không gian
5.1 Tính nhanh khoảng cách
5.2 Tìm hình chiếu vuông góc trong không gian
5.3 Thể tích khối đa diện, diện tích đa giác
5.4 Tính góc
Vấn để 6. Ứng dụng máy tính cầm tay vào bài toán trắc nghiệm liên quan đến số phức
6.1 Tính nhanh các phép toạn cơ bản số phức
6.2 Biểu diễn hình học của số phức
6.3 Giải phương trình
Sáng kiến kinh nghiệm dự thi cấp tỉnh Trang 5
NỘI DUNG
Phần 1.HƯỚNG DẪN SỬ DỤNG PHẦN MỀM ZIPGRADE CHẤM TRẮC NGHIỆM
BẰNG ĐIỆN THOẠI SMARTPHONE
Trong năm học 2016- 2017 đề thi THPT Quốc Gia môn Toán chuyển hình thức thi từ
tự luận sang trắc nghiệm. Với hình thức thi mới nhiều thầy (cô) còn cảm thấy bỡ ngỡ trong
nhiều khâu: dạy và học thế nào? Soạn và chấm đề trắc nghiệm ra sao?... Nhằm nâng cao chất
lượng kiểm tra đánh giá học sinh, chúng tôi muôn giới thiệu tới thầy (cô) phần mềm chấm trắc
nghiệm bằng ZipGrade. Với phần mềm này nhà trường và thầy (cô) có thể chấm trắc nghiệm
và quản lí điểm học sinh dễ dàng từ đó nâng cao chất lượng dạy và học phù hợp với những đổi
mới trong hình hình thức thi mới của chúng ta ngày nay. Đây là phần mềm hay phù hợp với tất
cả các môn thi trắc nghiệm nên chúng tôi thấy rằng cần được chia sẻ phần nào đó giảm được
vất vả khó khăn trong các kì thi hay đợt kiểm tra. Sau đây chúng tôi hướng dẫn chi tiết cài đặt
và sử dụng phần mềm và có hình ảnh minh họa. Để sử dụng phần mềm này chúng ta cần thực
hiện theo ba bước sau:
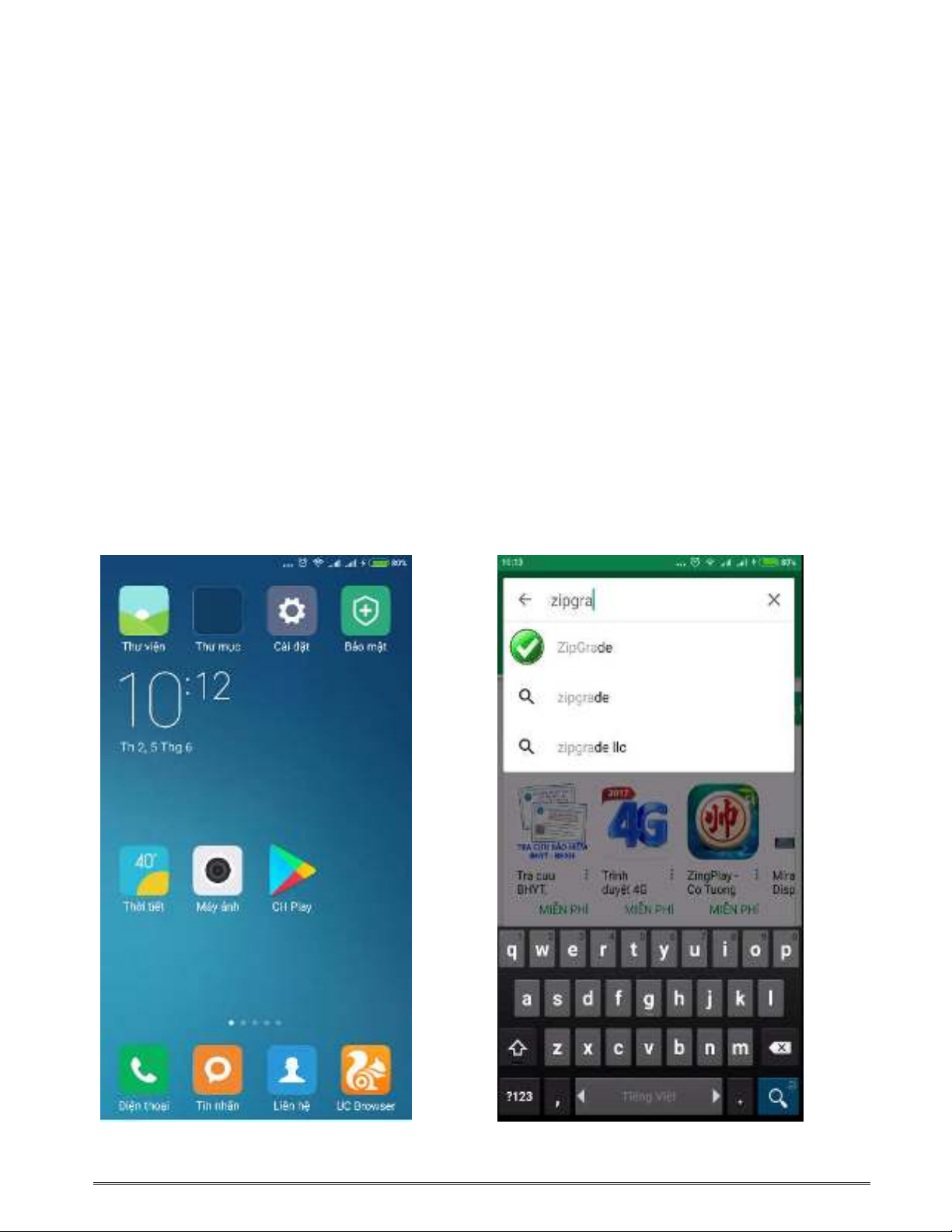
Bước 1.Cài đặt phần mềm.
Các thầy cô có thể vào CH Play và tìm kiếm với từ khóa “ ZipGrade”