52
Bµi 5: m¹ch sè häc
(Arithmetric circuits)
A. PhÇn tãm t¾t lý thuyÕt
1. Céng nhÞ ph©n (Binary Addition).
a) Nguyªn t¾c céng nhÞ ph©n :
Nguyªn t¾c 1 : 0 + 0 = 0
Nguyªn t¾c 2 : 0 + 1 = 1
Nguyªn t¾c 3 : 1 + 0 = 1
Nguyªn t¾c 4 : 1 + 1 = 0 vµ chuyÓn ®i 1 = 10
Nguyªn t¾c 5 : 1 + 1 + 1 = 1 vµ chuyÓn ®i 1 = 11
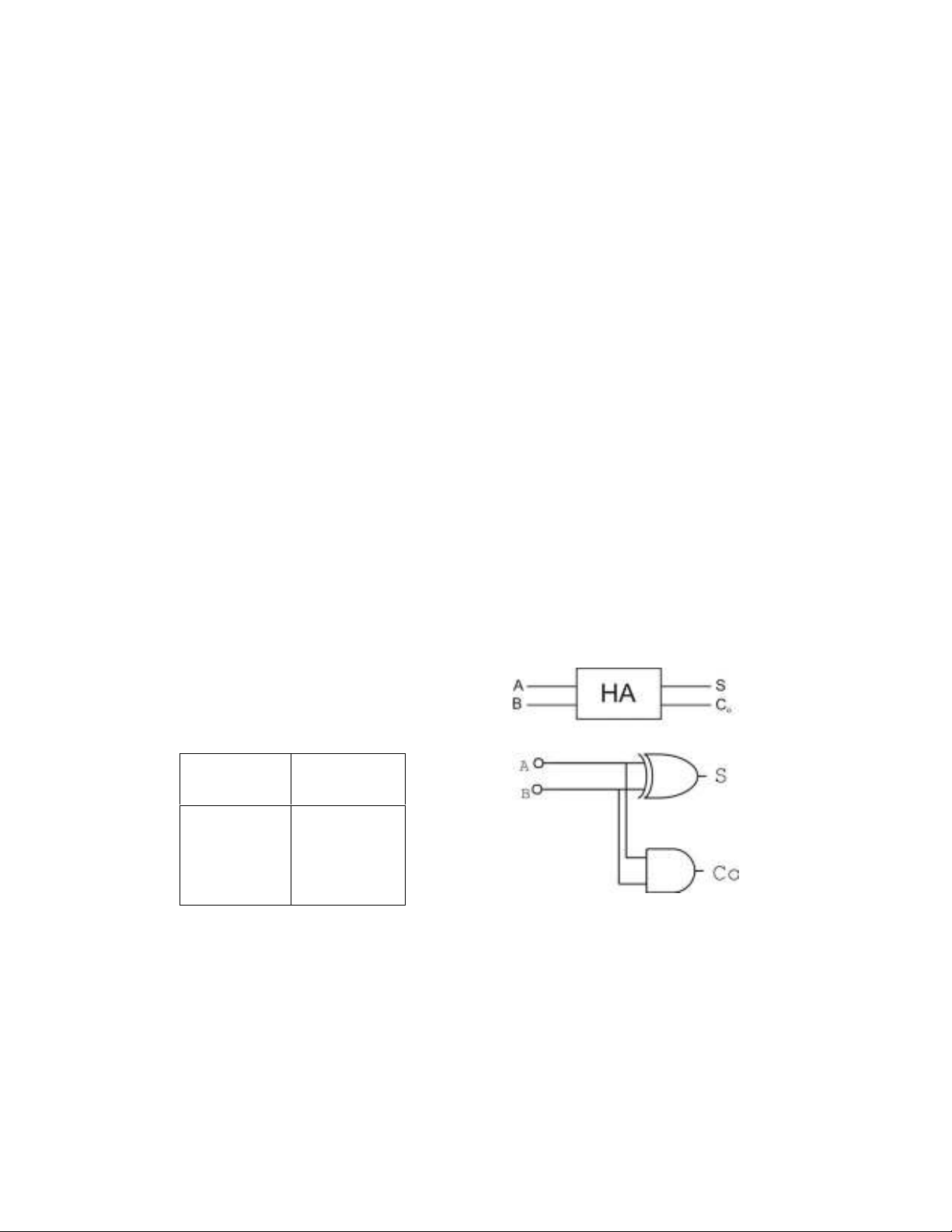
b) Tæng b¸n phÇn (Half Adder, viÕt t¾t HA).
M¹ch tæng b¸n phÇn cã hai ®Çu vµo lµ A vµ B, cã hai ®Çu ra lµ tæng S (Sum)
vµ chuyÓn ®i C0 (Carry - out). B¶ng ch©n lý, hµm logic vµ m¹ch logic sau ®©y dïng
cho m¹ch céng hai sè nhÞ ph©n 1 bit.
Hµm logic HA
S = A ⊕ B
C
0 = AB
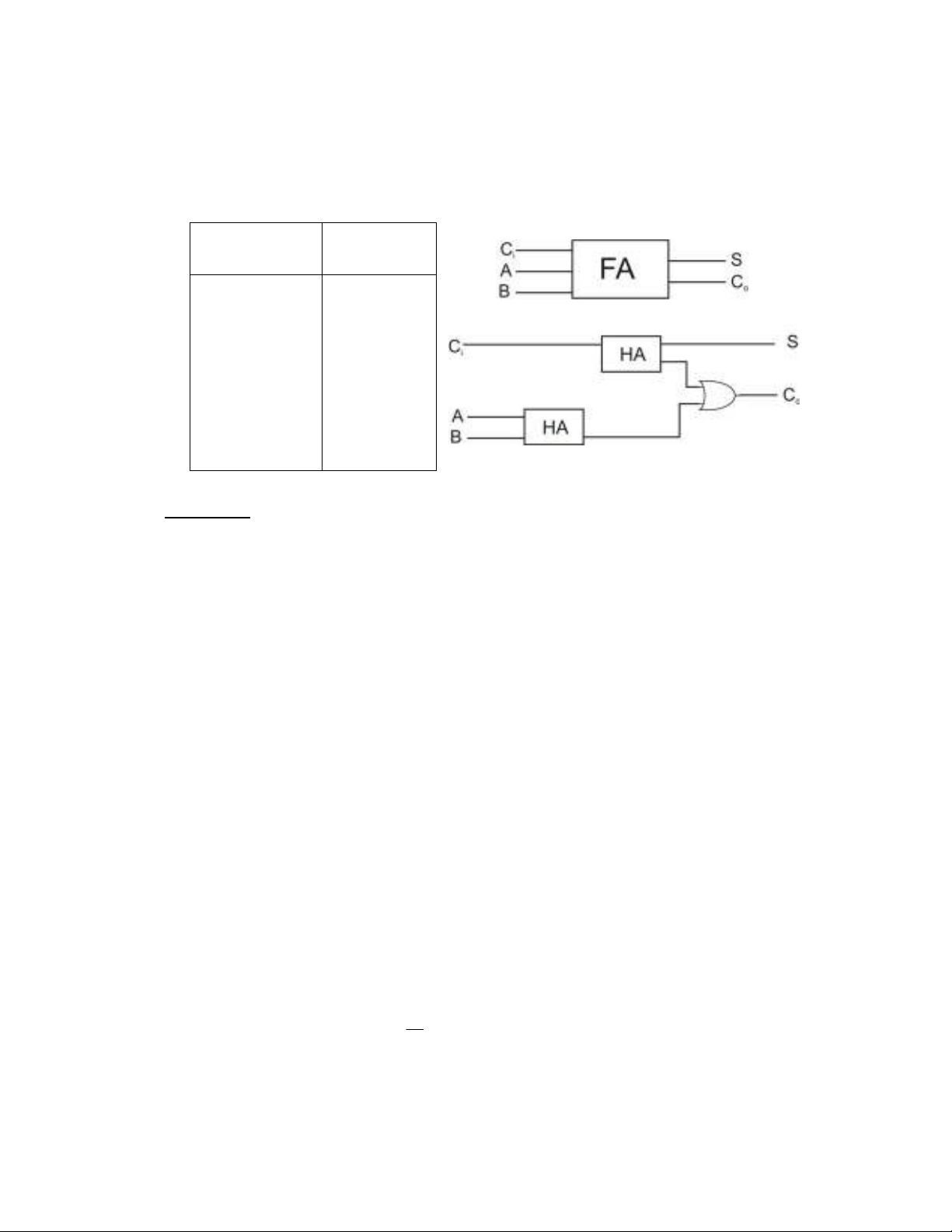
c) Tæng toµn phÇn (Full Adder, viÕt t¾t FA).
M¹ch tæng toµn phÇn cã ba ®Çu vµo lµ A, B, Ci (viÕt t¾t cña ch÷ Carry - in cã
nghÜa lµ chuyÓn néi bé hay chuyÓn trong).
Hai ®Çu ra lµ tæng S vµ ®−îc chuyÓn ®i C0. B¶ng ch©n lý, hµm logic vµ m¹ch
logic cho FA ®−îc tr×nh bµy d−íi ®©y dïng cho ba sè nhÞ ph©n 1 bit.
Hµm logic FA :
§Çu vµo
A B
§Çu ra
S C0
0 0
0 1
1 0
1 1
0 0
1 0
1 0
0 1
53
M¹ch logic FA x©y dùng tõ HA.
NhËn xÐt :
- Tõ m¹ch logic cña FA ta cã thÓ dÔ dµng thÊy r»ng m¹ch logic FA ®−îc
x©y dùng tõ hai m¹ch HA vµ thªm mét cöa hoÆc ë lèi ra C0.
- NÕu Ci = 0 (nèi ®Êt) th× m¹ch FA trë vÒ m¹ch HA.
2. Trõ nhÞ ph©n (Binary Subtraction)
a) Nguyªn t¾c trõ nhÞ ph©n :
Nguyªn t¾c 1 : 0 - 0 = 0
Nguyªn t¾c 2 : 0 - 1 = 1 vµ m−în 1
Nguyªn t¾c 3 : 1 - 0 = 1
Nguyªn t¾c 4 : 1 - 1 = 0
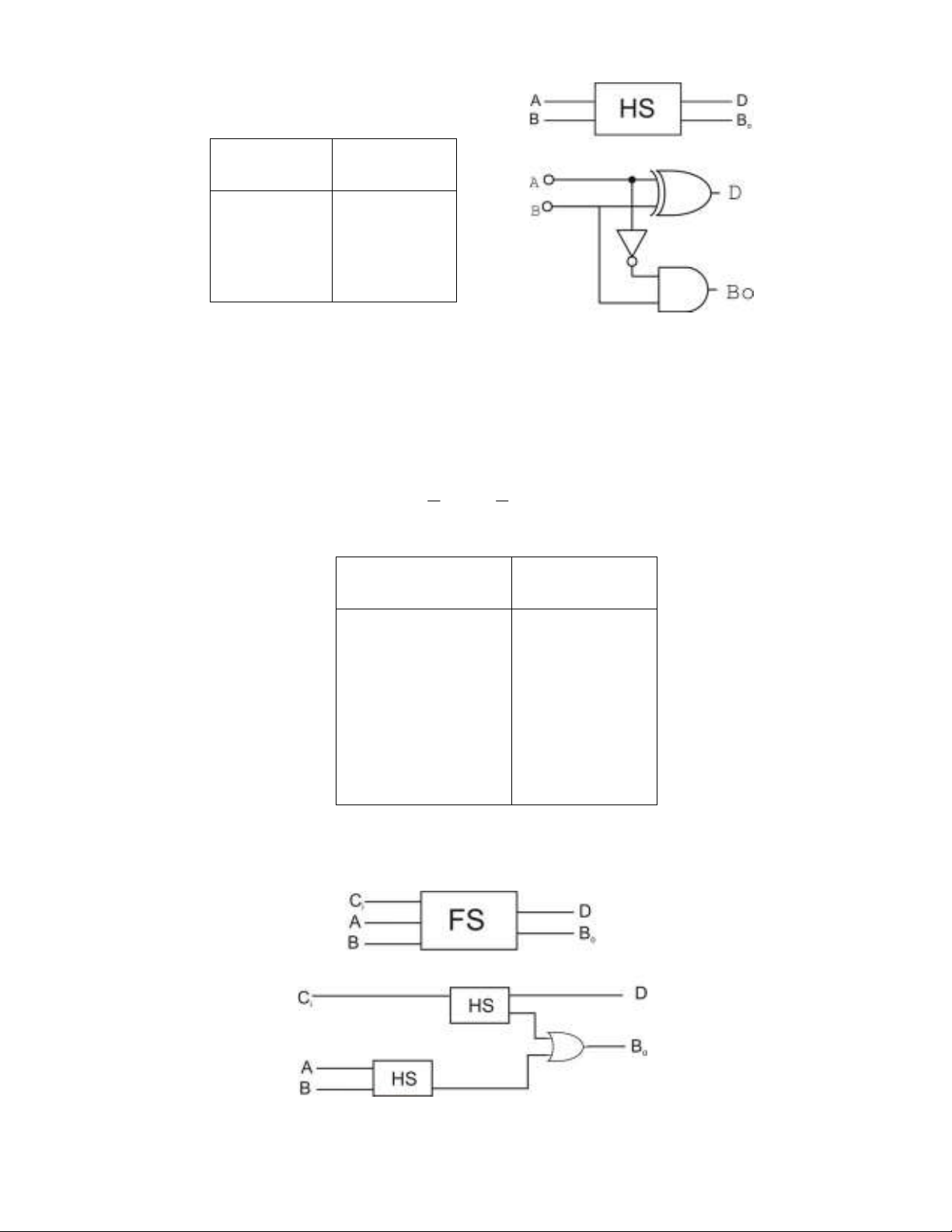
b) HiÖu b¸n phÇn (Half Subtractor, viÕt t¾t HS).
HiÖu b¸n phÇn lµ mét m¹ch logic thùc hiÖn trõ hai sè nhÞ ph©n 1 bit. §Çu vµo
lµ A vµ B , ®Çu ra lµ hiÖu D (Difference) vµ m−în ngoµi B0 (Borrow out). B¶ng
ch©n lý, hµm logic vµ m¹ch logic cho trªn h×nh sau:
Hµm logic HS :
So víi m¹ch HA ta thÊy m¹ch HS chØ kh¸c ë chç cã thªm cöa ®¶o ë ®Çu vµo
A cña cöa vµ.
§Çu vµo
A B Ci
§Çu ra
S C0
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0 0
1 0
1 0
0 1
1 0
0 1
0 1
1 1
ii
i
BCACABC
CB
A
S
++=
⊕
⊕
=
0
BAB
B
A
D
=
⊕
=
0
54
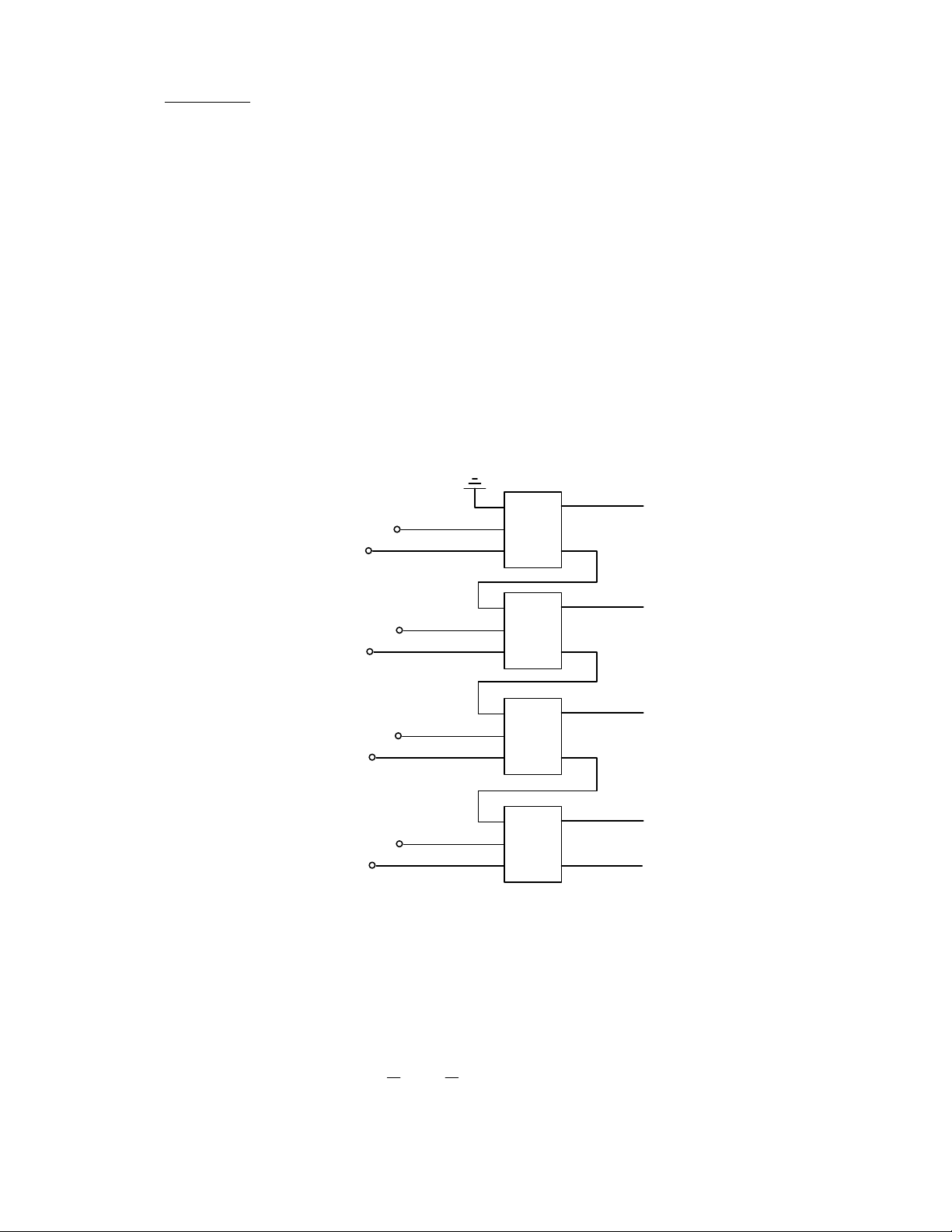
c) HiÖu toµn phÇn (Full Subtractor, viÕt t¾t FS)
M¹ch hiÖu toµn phÇn cã ba ®Çu vµo lµ A, B, Bi (viÕt t¾t cña ch÷ Borrow - in cã
nghÜa lµ m−în néi bé hay m−în trong). Hai ®Çu ra lµ hiÖu D vµ m−în ngoµi B0.
Hµm logic FS :
M¹ch logic FS x©y dùng tõ HS :
§Çu vµo
A B
§Çu ra
S C0
0 0
0 1
1 0
1 1
0 0
1 1
1 0
0 0
§Çu vµo
A B Bi
§Çu ra
D B0
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0 0
1 1
1 1
0 1
1 0
0 0
0 0
1 1
ii
i
BBBABAB
BB
A
D
++=
⊕
⊕
=
0
55
NhËn xÐt :
- Cã thÓ x©y dùng m¹ch FS tõ hai m¹ch HS vµ thªm mét cöa hoÆc ë lèi
ra B0.
- NÕu Bi = 0 (nèi ®Êt) th× FS trë vÒ HS.
3. M¹ch tæng hoÆc hiÖu hai sè nhÞ ph©n n bit (n bit Adder or Subtractor)
a) Tæng n bit
ë trªn ta míi nãi m¹ch tæng hai sè nhÞ ph©n 1 bit. Gi¶ sö cã hai sè nhÞ ph©n 4
bit A vµ B ( A = A4A3A2A1 vµ B4B3B2B1) cÇn céng víi nhau th× cÇn dïng bèn m¹ch
FA. L−u ý r»ng FA thø nhÊt cã Ci = 0 (low) lµm nhiÖm vô nh− HA . M¹ch tæng
m¾c theo kiÓu nµy gäi lµ tæng song song. Dùa trªn nguyªn t¾c nµy ta cã thÓ x©y
dùng m¹ch tæng song song n bit. C¸c ®Çu ra C0 cña FA thø nhÊt nèi víi Ci cña FA
thø hai, C0 cña FA thø hai nèi víi Ci cña FA thø ba ...
b) HiÖu n bit
M¹ch HS chØ kh¸c HA lµ cã thªm cöa ®¶o ë ®Çu vµo. VËy cã thÓ dïng HA
thay cho HS víi sù bæ sung kh«ng ®¸ng kÓ trong m¹ch. C©u hái ®Æt ra lµ cã thÓ
dïng FA thay thÕ FS ®−îc kh«ng? Muèn vËy, ta quay trë l¹i hµm logic FS vµ thùc
hiÖn mét sè biÕn ®æi to¸n häc.
i
BBAD
⊕
⊕
= (a)
ii0 BBBABAB ++= (b)
BiÕn ®æi (b) ta cã :
Co
S3
S2
S1
S0
B3
A3
B2
A2
B1
A1
B0
A0
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co
56
)
(
)
)
() ()
[]
ii0
iii0
iiii0
BBBABAB
BABBBABABBAB
BBBABABB.BA.BAB
++=
++=++=
+++==
Cßn (a) cã gi¸ trÞ t−¬ng tù :
ii BBABBAD ⊕⊕=⊕⊕=
Hµm logic viÕt cho FS sÏ lµ :
ii0
i
BBBABAB
BBAD
++=
+⊕=
So s¸nh víi hµm logic viÕt cho FA ta thÊy cã thÓ x©y dùng m¹ch FS tõ m¹ch
FA dÔ dµng. Muèn chuyÓn thµnh FS ta chØ cÇn m¾c thªm c¸c cöa ®¶o vµo c¸c
®Çu B, Bi vµ B0 nh− h×nh sau.
H×nh sau lµ bé trõ song song 4 bit (dïng 4 FA). Dùa trªn nguyªn t¾c nµy ta
x©y dùng m¹ch hiÖu n bit.
FS
FA
Bo
D
B
A
Bi
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co
Bo - x¸c ®Þnh dÊu
cña phÐp to¸n
D3
D2
D1
D0
+5V
B3
A3
B2
A2
B1
A1
B0
A0
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co
FA
Ci
A
B
S
Co