
Tiết 65 BÀI TẬP (tiếp).
A. CHUẨN BỊ:
I. Yêu cầu bài:
1. Yêu cầu kiến thức, kỹ năng, tư duy:
Nhằm giúp củng cố ôn luyện cho học sinh các kiến thức về phương pháp tính
tích phân đổi biến số dạng 1, dạng 2, tích phân từng phần
Thông qua bài giảng rèn luyện cho học sinh kĩ năng tính tích phân đổi biến số,
tích phân từng phần, kĩ năng tính toán, khả năng tư duy lô gíc, tư duy toán học dựa
trên cơ sở các kiến thức về tích phân.
2. Yêu cầu giáo dục tư tưởng, tình cảm:
Qua bài giảng, học sinh say mê bộ môn hơn và có hứng thú tìm tòi, giải quyết
các vấn đề khoa học.
II. Chuẩn bị:
Thầy: giáo án, sgk, thước.
Trò: vở, nháp, sgk và đọc trước bài.
B. Thể hiện trên lớp:
I. Kiểm tra bài cũ: 3’
CH:
Nêu quy tắc tính tích phân từng phần
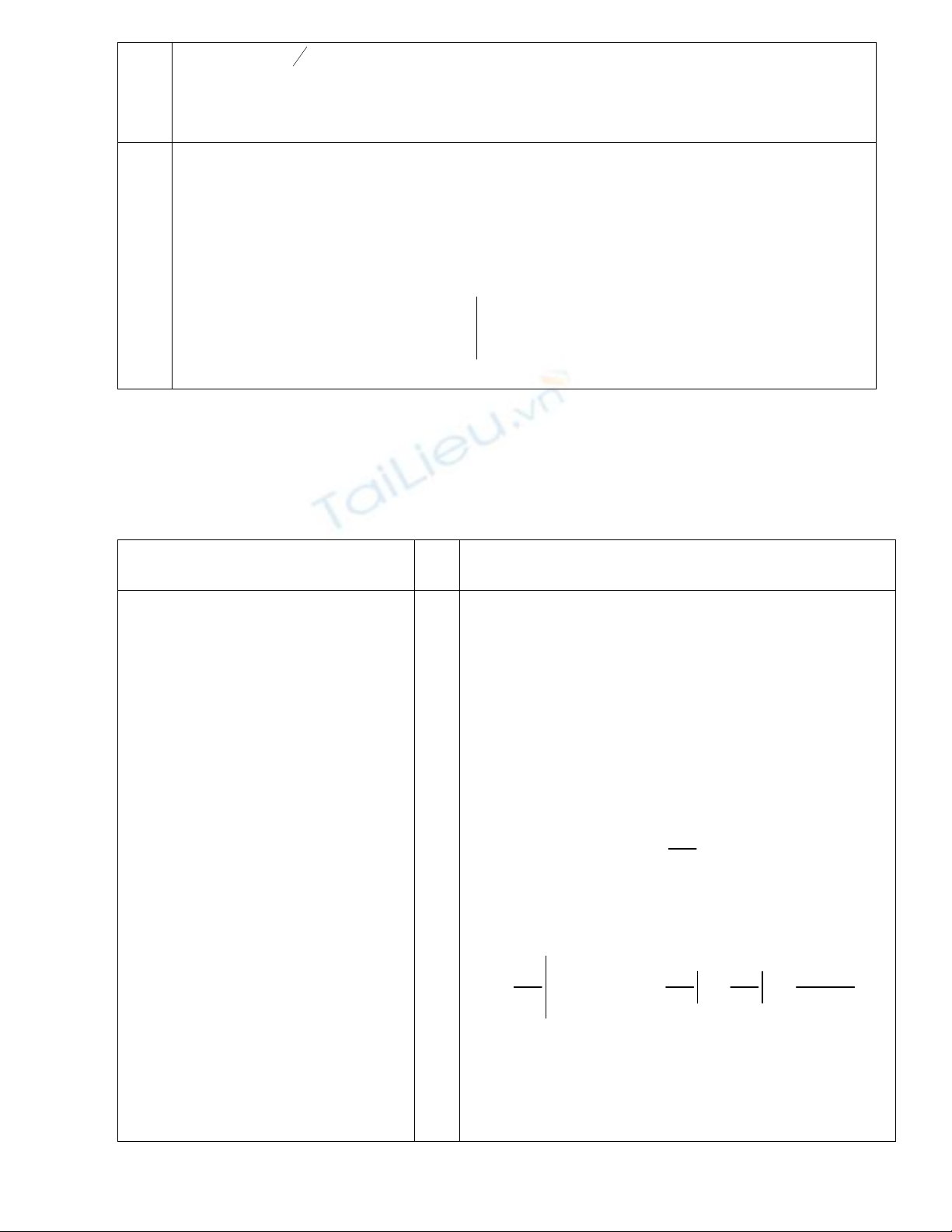
áp dụng: A= 2
0
xsin xdx
ĐA:
Quy tắc:
+ Biểu diễn f(x)=udv
+Tính v và du
+ Thay vào công thức:
b b
b
a
a a
udv uv vdu
II. Bài giảng:
Phương pháp tg Nội dung
Hs nhận dạng tích phân và nêu
phương pháp tính?
học sinh giải?
19
Bài 5
Tính các tích phân :
A= 13x
0
xe dx
Đặt:
3x
3x
du dx
u x
e
dv e v
3
Do đó:
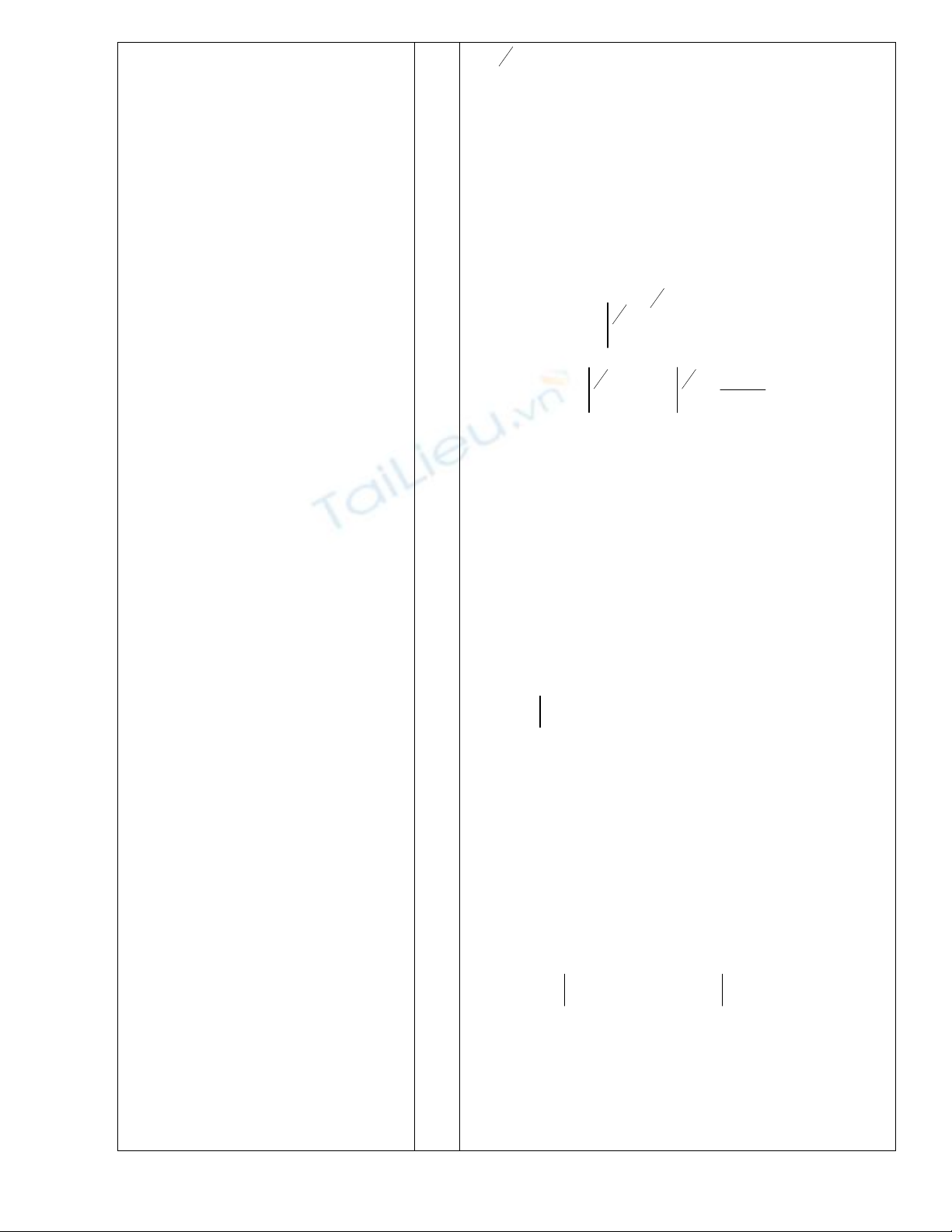
A= 1
3x 3x 3x 3
1 3x 1 1
0 0 0
0
e e e 2e 1
x e dx x
3 3 9 9
Hs giải?
GV HD học sinh sử dụng tích
phân từng phần hai lần.
học sinh giải?
B=
2
0
x 1 cosxdx
Đặt:
u x 1 du dx
dv cosxdx v sin x
Do đó:
2
2
0
0
2 2
0 0
B x 1 sin x sin xdx
4
x 1 sinx cosx
2
C= 12 x
0
x .e dx
Đặt :
2
x
x
du 2xdx
u x
v e
dv e dx
Ta có:
C= 1
2 x 1 x
0 1
0
x e 2 e xdx e 2C ;
với
1x
1
0
C e xdx
Tính C1: x x
u x du dx
dv e dx v e
C1=1
2 1 x x 1
0 0
0
x e e dx e e 1
Do đó C1=e-2.1=e-2
Bài 6: Tính các tích phân

Hs nhận dạng bài tập và nêu
phương pháp giải?
học sinh áp dụng?
Sau khi tính tích phân từng
phần 1 lần thì thu được kết quả
có gì đặc biệt? có phải tính
tính phân từng phần thêm nữa
không?
22
I= 2x
0
e cosxdx
Đặt:
x x
du e u e
v cosxdx dv sin x
2
x x
2 2
0 1
0
I e sin x e sin xdx e I
Tính I1
Đặt:
x x
u e du e dx
dv sin xdx v cosx
2
x x
2
1 0
0
I e cosx e cosxdx 1 I
Do đó:
2 2
2
I e 1 I 2I e 1
e 1
I
2
J=
5
2
2xln x 1 dx
Đặt:
2
dx
duu ln x 1
x 1
dv 2xdx v x
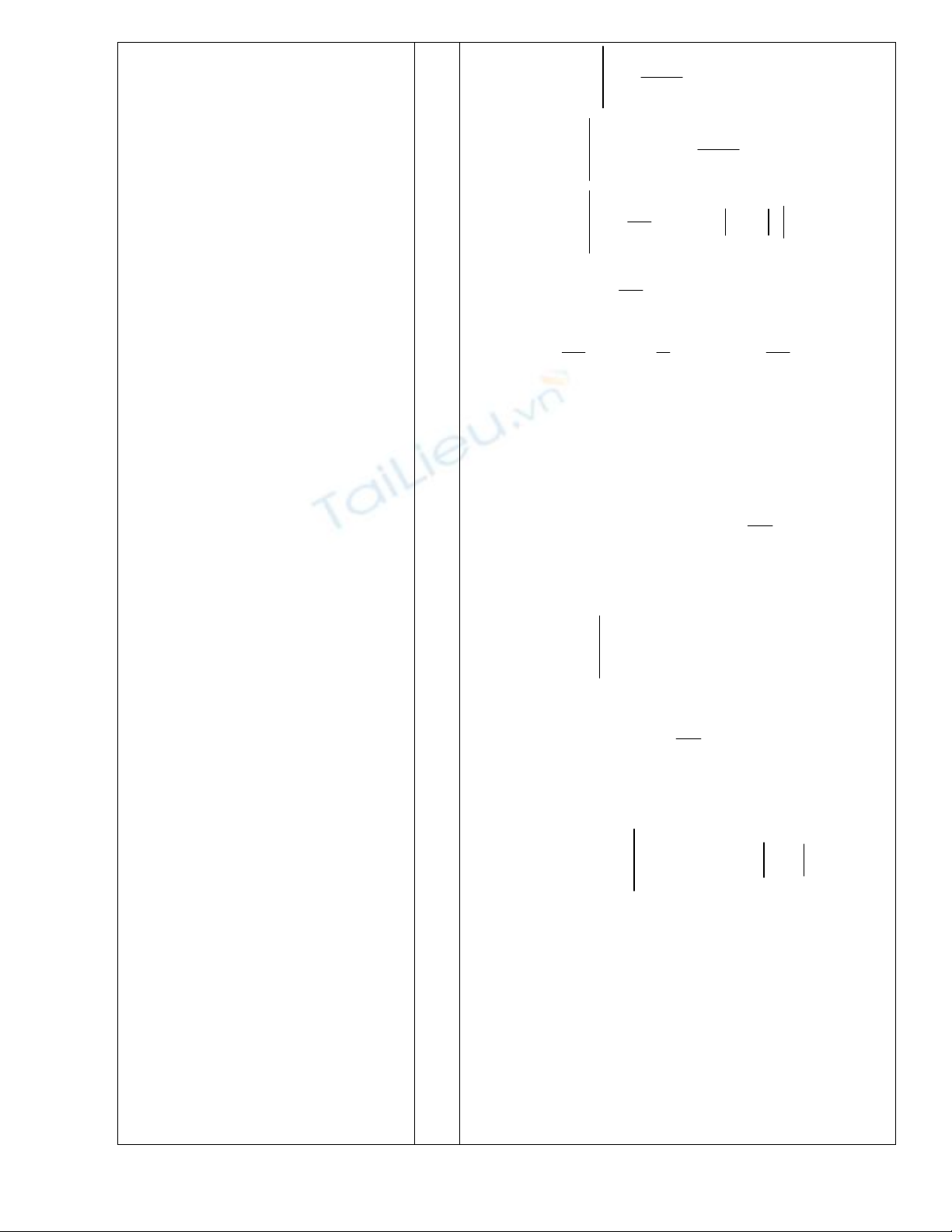
Hs giải?
52
2 5
2
2
5
2 5
2
2
2
2 5 5
2 2
x
J x ln x 1 dx
x 1
1
x ln x 1 x 1 dx
x 1
x
x ln x 1 x ln x 1
2
25
25ln4 ln1 5 ln4 4 ln1
2
35 8 43
25ln4 ln4 24ln4
2 2 2
C=
e2
1
ln x dx
Đặt:
2
dx
du 2lnx
u ln x
x
dv dx v x
C=
e
2e
1
1
x ln x 2 ln xdx
Đặt:
dx
u ln x du
x
dv dx
v x
e e
e e e
1 1 1
1 1
lnxdx xln x dx xln x x
Vậy
C=
2
e lne ln1 2 elne ln1 e 1 e 2
















