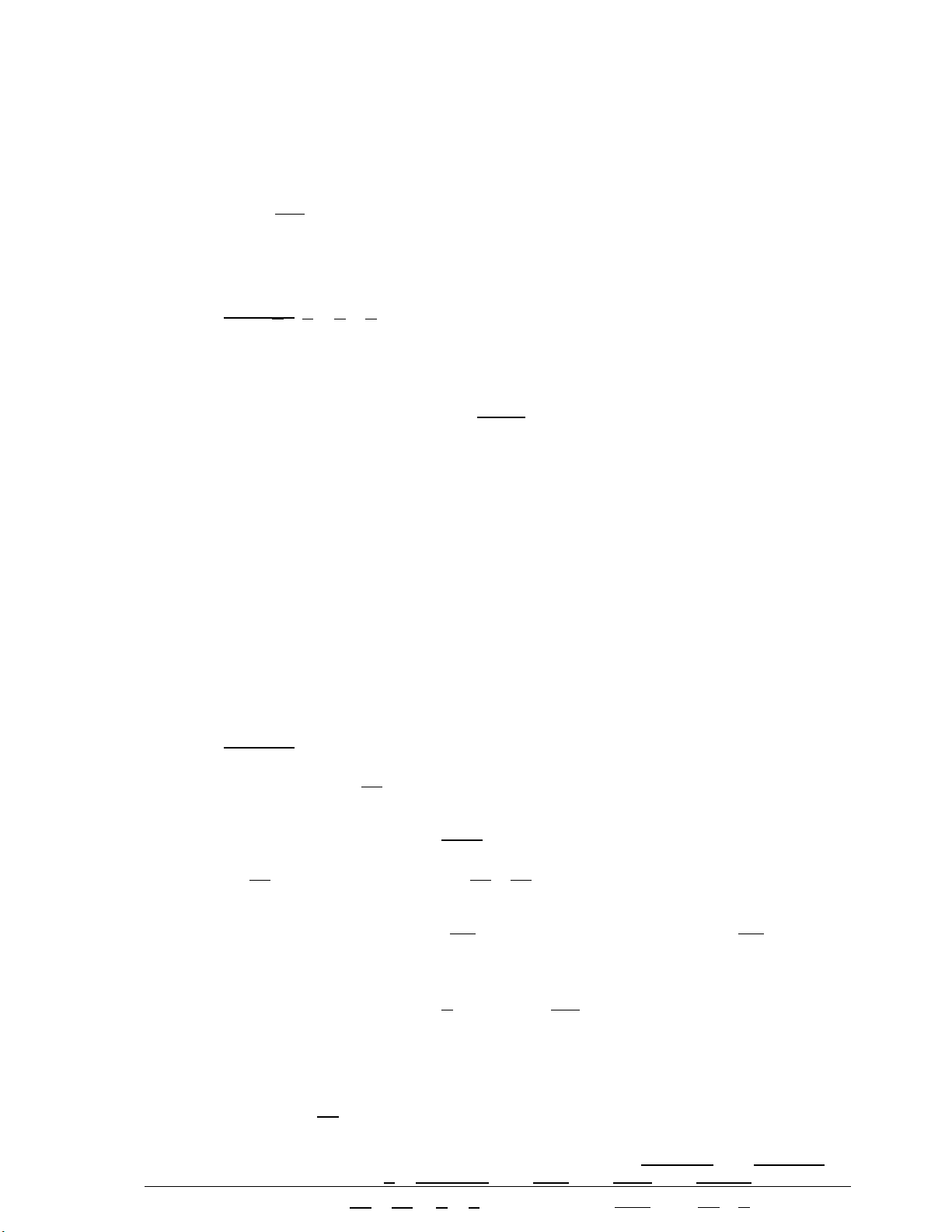
CHUYÊN Đ CH NG MINH B T ĐNG TH CỀ Ứ Ấ Ẳ Ứ
C huyên đ 4:ề
C¸c ph¬ng ph¸p chøng minh
bÊt ®¼ng thøc
A. KiÕn thøc c¬ b¶n.
* Mét sè bÊt ®¼ng thøc cÇn nhí:
1. a2 0; ; -
, dÊu " = " x¶y ra khi vµ chØ khi ab 0
2. BÊt ®¼ng thøc C« - si : a, b 0
dÊu " = " x¶y ra vµ chØ khi a = b
3. BÊt ®¼ng thøc Bunhiac«pxki:
(a.c + b.d)2 (a2 + b2) (c2 + d2), dÊu " = " x¶y ra khi vµ chØ khi
B. C¸c ph ¬ng ph¸p chøng minh bÊt ®¼ng thøc .
Ph ¬ng ph¸p 1 : Dùa vµo ®Þnh nghÜa.
A B <=> A - B 0
Chó ý c¸c h»ng ®¼ng thøc:
* a2 + 2ab + b2 = (a + b)2 0;
* a2 + b2 + c2 + 2ab + 2ab + 2ca = (a + b + c)2 0
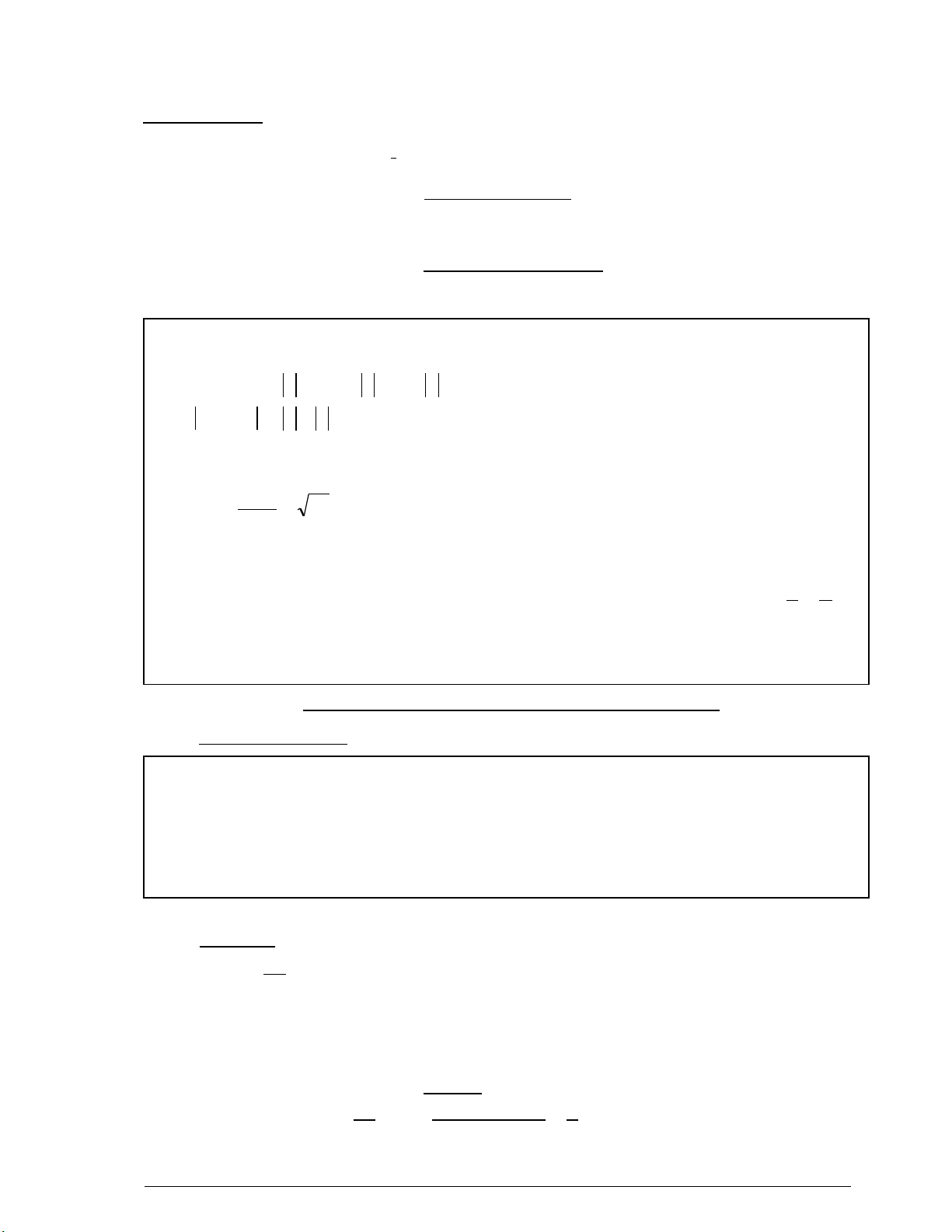
Bµi 1.1: Chøng minh r»ng víi mäi x, y ta lu«n cã:
a.
b. x2 + y2 + 1 xy + x + y;
c. x4 + y4 xy3 +x3y
Gi¶i:
a. XÐt hiÖu:
1
0
a
aaa
ba
ba
,
2ab
ba
d
b
c
a
;
4
2
2xy
y
x
0)2(
4
1
4
44
4
2
222
2
yx
yxyx
xy
y
x
0)2(
4
1
4
44
4
2
222
2
yx
yxyx
xy
y
x
CHUYÊN Đ CH NG MINH B T ĐNG TH CỀ Ứ Ấ Ẳ Ứ
VËy: DÊu "=" x¶y ra khi vµ chØ khi 2x = y.
b. x2 + y2 + 1 - (xy + x + y) =
0
VËy: x2 + y2 + 1 xy + x + y.
c. x4 + y4 - (xy3 + x3y) = x4 - xy3 + (y4 - x3y)
= x (x3 - y3) - y (x3 - y3) = (x3 - y3) (x - y)
= (x - y)2 (x2 + xy + y2)
= (x - y)2 0
VËy: x4 + y4 xy3 + x3y
Bµi 1.2: Cho 0 < a b c. Chøng minh r»ng:
a.
b.
Gi¶i:
a.
=
=
=
= ( v× o < a b
c)
VËy:
b.
2
.
4
2
2xy
y
x
222
)1()1()(
2
1
xyyx
4
3
)
2
(
2
2yy
x
c
a
b
c
a
b
a
c
c
b
b
a
b
a
a
b
c
b
a
c
)(
1222222 baaccbbcabca
abcc
a
b
c
a
b
a
c
c
b
b
a
)()()(
1222222 acbcbaabcbca
abc
)()()(
1222 abcababbac
abc
))((
12
cabcbcaab
abc
2
)((
1cababcaab
abc
0))()((
1 acbcab
abc
c
a
b
c
a
b
a
c
c
b
b
a
)(
12222 cacbabbc
abcb
a
a
b
c
b
a
c
)(
1222 abccbabbc
abc
)()(
1
)()(
1222 cbbabcbc
abc
abcabcbbc
abc
CHUYÊN Đ CH NG MINH B T ĐNG TH CỀ Ứ Ấ Ẳ Ứ
(V× a2c abc)
(V× o < a b c).
VËy:
Bµi 1.3: Cho a < b < c < d. H·y xÕp thø tù t¨ng dÇn c¸c sè sau:
x = (a + b) (c + d); y = (a + c) (b + d); z = (a + d) (b + c).
Gi¶i:
XÐt hiÖu: y - x = (a + b) (b + d) - (a + b) (c + d)
= ab + ad + cb + cd - ac - ad - bc - bd
= b (a - d) - c (a - d)
= (a - d) (b - c) > 0 (v× a < b < c < d)
Suy ra: y > z
T¬ng tù, xÐt hiÖu: z - y = (a + d) (b + c) - (a + c) (b + d)
= (a - b) (c - d) > 0
Suy ra: z > y.
VËy: x < y < z.
Bµi 1.4: Cho abc = 1 vµ a3 > 36. Chøng minh r»ng:
Gi¶i
(V× abc = 1
vµ a3 > 36 nªn a > 0).
VËy:
3
0))((
1 acbcb
abc
b
a
a
b
c
b
a
c
cabcabcb
a 22
2
3
cabcabcb
aa
cabcabcb
a 22
22
22
2
1243
bc
a
bccaabcb
a3
12
2
4
2
22
2
0)36(
12
1
2
3
2
a
a
cb
a
cabcabcb
a 22
2
3
22 1
1
,
1
1
bb
b
y
aa
a
a
aa
a
a
a
a
aa
x11
1
1
1
1
1
1
1
1
11
22
22
)
1111
22 ba
va
ba
CHUYÊN Đ CH NG MINH B T ĐNG TH CỀ Ứ Ấ Ẳ Ứ
Bµi 1.5: Cho a > b > 0. So s¸nh hai sè x, y víi x =
Gi¶i:
Ta cã x,y > 0 vµ
(V× a > b> 0 nªn
VËy: x < y.
Ph ¬ng ph¸p 2 : Sö dông tÝnh B¾c CÇu:
* A B
=> A C.
B C
* 0 x 1 => x2 x (v× x - x2 = x (1 - x) 0)
Bµi 2.1: Cho 0 x, y, x 1, Chøng minh r»ng:
a. 0 x + y + z - xy - yz - zx 1;
b. x2 + y2 + z2 1 + x2y + y2z + z2x.
Gi¶i:
a. Ta cã: x + y + z - xy - yz - zx = x (1 - y ) + y (1 - z) + z (1 - x) 0
(1)
MÆt kh¸c: (1 - x) (1 - y) (1 - z) = 1 - x- y - z + xy + yz + zx - xyz 0,
Suy ra: x + y + z - xy - yz - zx 1 - xyz 1
(2)
Tõ (1) vµ (2) suy ra: 0 x + y + z - xy - yz - zx 1.
b. Ta chøng minh: x2 + y2 + z2 - x2y - y2z - z2x 1.
Ta cã: x2 + y2 + z2 - x2y- y2z - z2x = x2 (1 - y) + y2 (1 - z) + z2 (1 - x)
x (1 - y) + y (1 - z) + z (1 - x) (v× x2 x, y2 y, z2 z)
x + y +z - xy - yz - zx 1 (c©u a).
Bµi 2.2: Cho a, b, c lµ ®é dµi ba c¹nh cña tam gi¸c cã chu vi b»ng 2.
Chøng minh r»ng : a2 + b2 + c2 + 2abc < 2.
Gi¶i:
NÕu a 1 th× tõ b + c 1 suy ra a + b + c > 2, v« lý! VËy 0 < a < 1
T¬ng tù: 0 < b < 1, 0 < c < 1.
4
y
b
b
1
11
1
1
2
CHUYÊN Đ CH NG MINH B T ĐNG TH CỀ Ứ Ấ Ẳ Ứ
Ta cã: (1 - a) (1 - b) (1 - c) = 1 - a - b - c + ab + bc + ca - abc > 0,
suy ra
abc < ab + bc + ca - 1 (v× a +b + c = 2) (1)
Mµ 4 = (a + b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca), suy ra:
ab + bc + ca = 2 - (2)
Tõ (1) vµ (2) suy ra:
abc < 1 -
Bµi 2.3: Cho 0 < a, b, c, d < 1. Chøng minh r»ng:
(1 - a) (1 - b) (1 - c) (1 - d) > 1 - a - b - c - d
Gi¶i:
Ta cã: (1 - a) (1 - b) = 1 - a - b + ab > 1 - a - b (1)
V× 1 - c > 0 nªn:
(1 - a) (1 - b) (1 - c) > (1 - a - b) (1 - c) (2)
(1 - a - b) (1 - c) = 1 - a - b - c + c (a + b) > 1 - a - b - c (3)
Tõ (2) vµ (3) suy ra: (1 - a) (1 - b) (1 - c) > 1 - a - b - c
VËy: (1 - a) (1 - b) (1 - c) (1 - d) > (1 - a - b - c) (1 - d) > 1 - a - b - c -
d
(V× d (a + b + c) > 0)
Bµi 2.4: Cho 0 a, b, c 2 tho¶ a + b + c = 3. Chøng minh r»ng:
a2 + b2 + c2 5
Gi¶i:
C¸ch 1: V× a + b + c = 3 nªn cã Ýt nhÊt mét trong ba sè a, b, c
kh«ng nhá
h¬n 1, gi¶ sö a 1.
V× 1 a 2 nªn: (a - 1) (a - 2) = a2 - 3a + 2 0 => a (3 - a) 2
Suy ra: ab + bc + ca = a (b + c) + bc = a (3 - a) + bc 2 (1)
VËy: a2 + b2 + c2 = (a + b + c)2 - 2 (ab + bc + ca)
= 9 - 2 (ab + bc + ca) 5 (theo (1))
C¸ch 2: V× a, b, c 2 nªn:
(2 - a) (2 - b) (2 - c) = 8 - 4 (a + b + c) + 2 (ab + bc + ca) - abc 0
5
)(
2
1222 cba
22)(
2
1222222
abccbacba
2
2
abc