Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Phương pháp giải:
Để xác định góc giữa hai mặt phẳng (P) và (Q) ta thực hiện như sau:
+) Xác định giao tuyến
( ) ( )
∆ = ∩
P Q
+) Tìm mặt phẳng trung gian (R) mà (R) ⊥ ∆, (Đây là bước quan trọng nhất nhé!)
+) Xác định các đoạn giao tuyến thành phần:
( )
( )
( ) ( )
( );( ) ;
( ) ( )
= ∩
⇒=
= ∩
a R P
P Q a b
b R Q
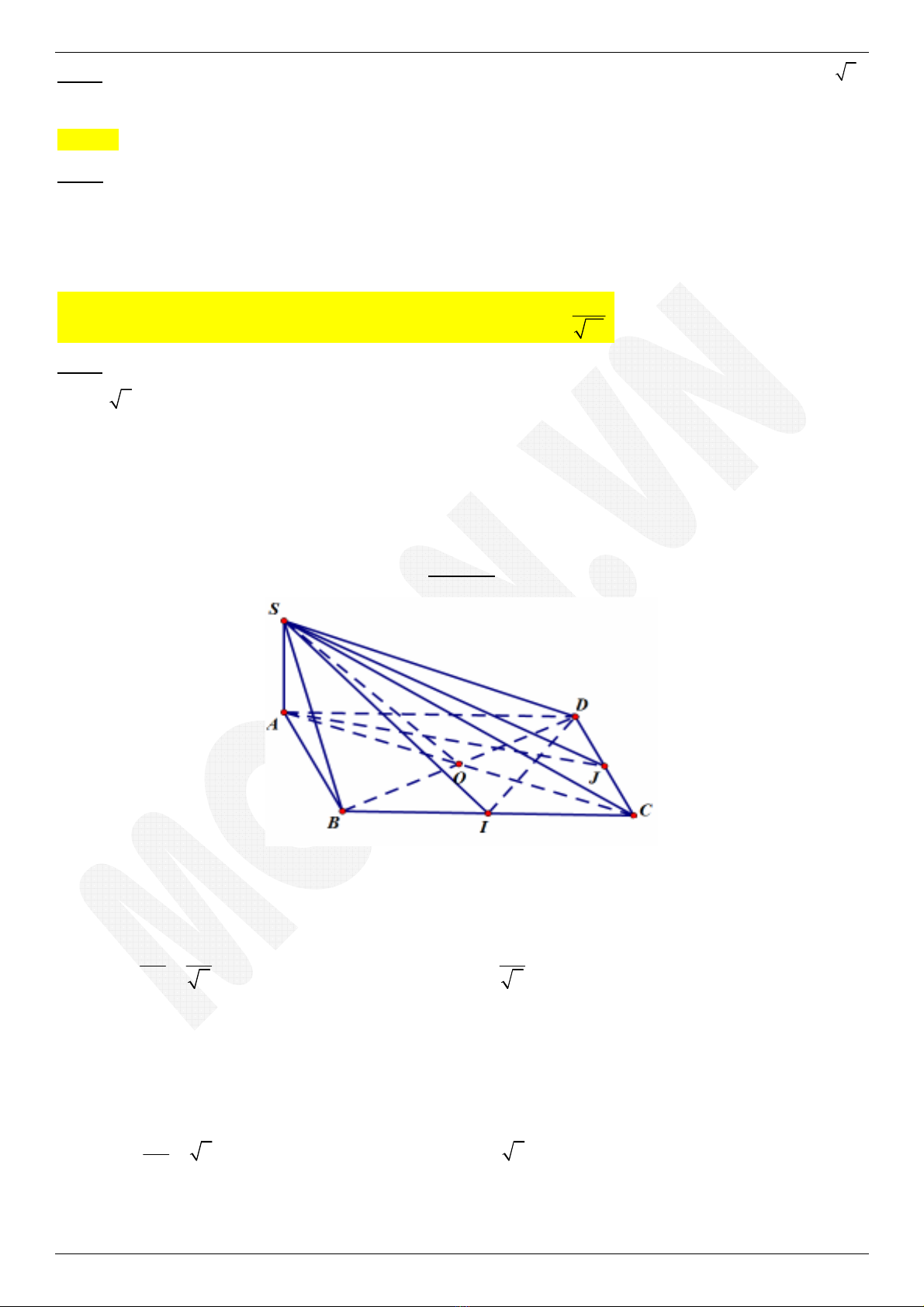
Ví dụ 1. [ĐVH]: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, O là tâm đáy. Hình chiếu
vuông góc của S xuống (ABCD) là trung điểm H của OA. Biết
(
)
; 60
=SD ABCD
. Tính góc giữa
a) (SCD) và (ABCD).
b) (MBC) và (ABCD), với M là trung điểm của SA.
Đ/s:
30 30
) tan φ; ) tan φ
6 14
= =a b
Ví dụ 2. [ĐVH]:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B với AB = BC = a; AD =
5a/2. Hình chiếu vuông góc của S xuống (ABCD) là điểm H thuộc AB với BH = 2AH. Biết
(
)
0
; 45
=SC ABCD
. Tính góc giữa
a)
(SCD) và (ABCD).
b)
(IBC) và (ABCD), với I thuộc đoạn SA sao cho SI = 2IA.
Ví dụ 3. [ĐVH]:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, I là điểm trên đoạn BC sao cho CI =
2BI. Hình chiếu vuông góc của S lên mặt phẳng ABC là điểm H thuộc AI với
2 0
+ =
HA HI
, biết
(
)
0
; 60
=SB ABC
. Tính góc giữa hai mặt phẳng (NAB) và (ABC) với N là trung điểm của SI.
BÀI TẬP TỰ LUYỆN
Bài 1.
[ĐVH]:
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và
2,
=SA a
đ
áy ABCD là hình thang vuông t
ạ
i A
và D v
ớ
i AB = 2a, AD = DC = a. Tính góc gi
ữ
a các c
ặ
p m
ặ
t ph
ẳ
ng sau:
a) (SBC) và (ABC).
b) (SAB) và (SBC).
c)* (SBC) và (SCD).
Đ/s: a) 45
0
b) 60
0
c)
6
cos
α
3
=
04. GÓC GIỮA HAI MẶT PHẲNG – P1
Th
ầy Đặng Việt H
ùng
[ĐVH]
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Bài 2. [ĐVH]: Cho tứ diện ABCD có ABC là tam giác đều, ∆DBC vuông cân tại D. Biết
2 , 7
= =
AB a AD a
.
Tính góc giữa (ABC) và (DBC).
Đ/s: 30
0
Bài 3. [ĐVH]: Cho hình chóp SABC, có đáy ABC là tam giác vuông cân với BA = BC = a; SA ⊥ (ABC) và
SA = a. Gọi E, F lần lượt là trung điểm của các cạnh AB và AC.
a) Tính góc giữa hai mặt phẳng (SAC) và (SBC).
b) Tính góc giữa 2 mặt phẳng (SEF) và (SBC).
Đ/s: a)
(
)
0
( ),( ) 60
=SAC SBC
b)
3
cos(( ), ( )) .
10
=SEF SBC
Bài 4.
[ĐVH]:
Cho hình chóp S.ABCD có
đ
áy ABCD là hình vuông c
ạ
nh 2a, SA vuông góc v
ớ
i
đ
áy và
2.
=SA a Tính góc gi
ữ
a
a)
(SCD) và (ABCD).
b)
(SBD) và (ABCD).
c)
(SDI) và (ABCD), v
ớ
i I là trung
đ
i
ể
m c
ủ
a BC.
Lời giải:
a) Ta có:
( ) ( ) ( )
(
)
( )
, ,
⊥
⇒
⊥
⇒
= =
⊥
CD SA
CD SAD ABCD SCD SD SA SDA
CD AD
( ) ( )
( )
1 1
tan , arctan
2 2
SA
SDA ABCD SCD SDA
SD
= =
⇒
= =
b)
(SBD) và (ABCD).
Ta có:
( ) ( ) ( )
( )
( )
( )
, , 90
o
BD AC BD SAC ABCD SBD SO AC AOS doAOS
BD SA
⊥
⇒
⊥
⇒
= = <
⊥
( ) ( )
( )
tan 2 , arctan 2
SA
AOS ABCD SBD AOS
OA
= = ⇒= =
c)
(SDI) và (ABCD), v
ớ
i I là trung
đ
i
ể
m c
ủ
a BC.
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
Gọi J là trung điểm của CD
Ta có:
( ) ( ) ( )
( )
( )
, ,
DI JA
DI SJA ABCD SDJ SJ JA SJA
DI SA
⊥
⇒⊥⇒= =
⊥
( ) ( )
( )
2 2
1 1
tan , arctan
3 3
SA SA
SJA ABCD SDJ SJA
JA AD DJ
= = = ⇒= =
+
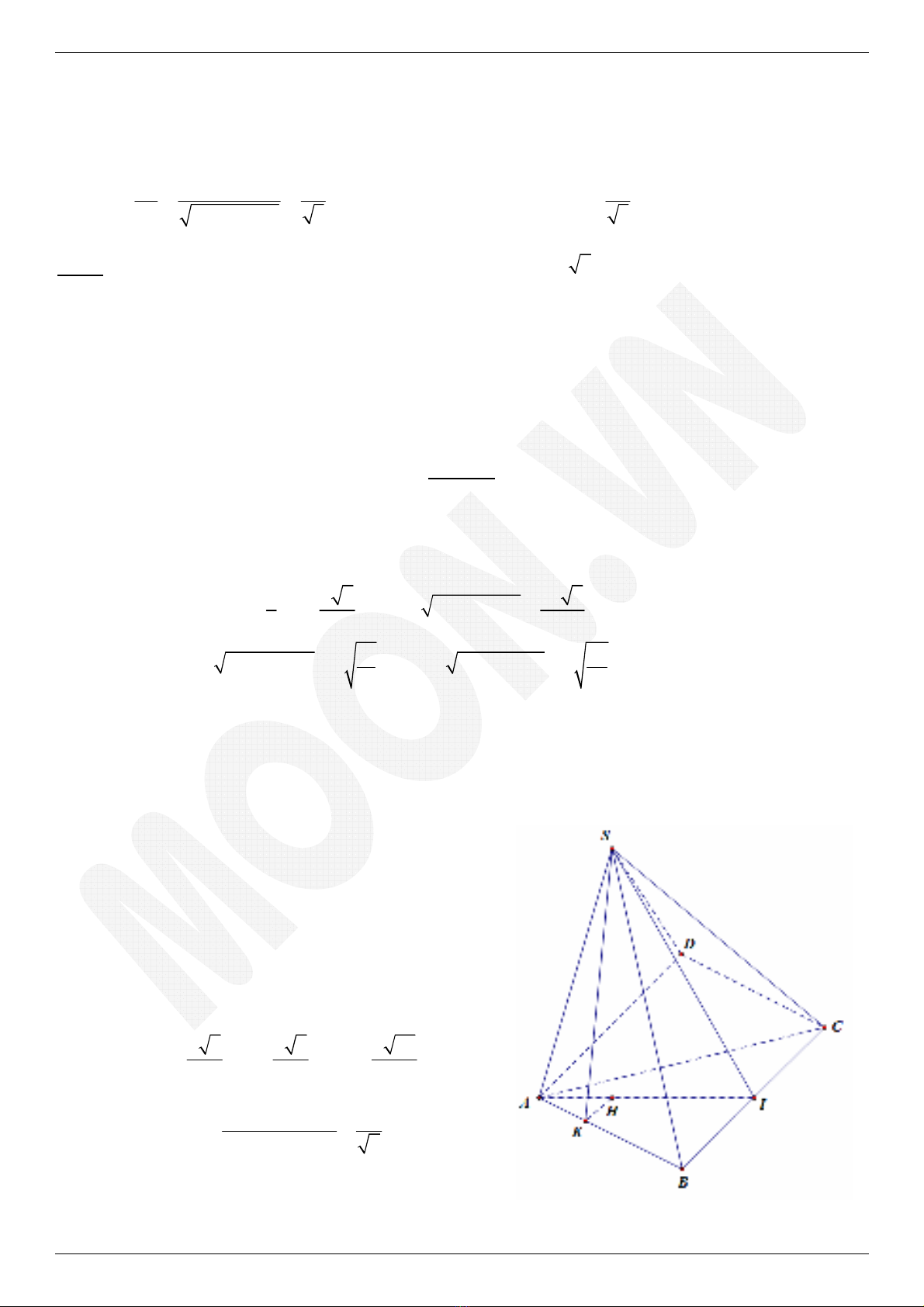
Bài 5. [ĐVH]: Cho hình chóp S.ABC có đáy là tam giác đều cạnh
2
a
, I là trung điểm của BC. Hình chiếu
vuông góc của S lên mặt phẳng ABC là điểm H thuộc AI với
2 0
+ =
IH AH
và SH = 2a. Tính góc giữa
a) BC và SA.
b) (SBC) và (ABC).
c) (SAB) và (ABC).
Lời giải:
a) Tính góc giữa BC và SA
Dựng hình thoi ABCD
( ) ( )
/ / ;
BC AD SAD BC SA SAD
⇒∈⇒=
Do
2 2
1 6 5 6
2 0
3 6 6
a a
AH IH AH AI SA SH AH+ = ⇒= = ⇒= + =
Xét: 2 2 2 2
13 37
:
6 6
vAHD HD AD AH a SD SH HD a∆ = + = ⇒= + =
Nh
ậ
n xét:
{ }
2 2 2
90
o
SA AD SD SAD A SAD+ = ⇒∆ ⊥ ⇒=
V
ậ
y
( )
; 90
o
BC SA =
b)
Tính góc gi
ữ
a
(
)
(
)
và
SBC ABC
Ta có:
(
)
(
)
SBC ABC BC
∩ =
Nh
ậ
n xét:
SBC
∆
cân t
ạ
i
S
SI BC
⇒⊥
,
Mà
(
)
AI BC BC SAI
⊥⇒⊥
Suy ra:
( ) ( )
( )
( )
; ;
SBC ABC SI AI SIA
= =
Tính
đượ
c:
6 6 42
;
2 3 3
a a a
AI HI SI= = ⇒=
Xét:
2 2 2
1
: cos 67,8
2 . 7
o
SI IA SA
SAI SIA SIA
SI IA
+ −
∆ = = ⇒=
Suy ra:
( ) ( )
( )
; 67,8
o
SBC ABC =
Khóa học Toán Cơ bản và Nâng cao 11 – Thầy ĐẶNG VIỆT HÙNG Facebook: LyHung95
Tham gia khóa Toán Cơ bản và Nâng cao 11 tại MOON.VN để có sự chuẩn bị tốt nhất cho kì thi THPT quốc gia!
c) Tính góc giữa
(
)
(
)
và
SAB ABC
Ta có:
(
)
(
)
SAB ABC AB
∩ =
Từ H dựng
( ) ( ) ( )
( )
;
HK AB AB SHK SAB ABC SKH
⊥⇒⊥⇒=
Ta dễ dàng tính được:
2 2
1 2 146
;
3 6 6
a a
HK BI SK SH HK= = = + =
Xét:
2 2 2
1
:cos 83,3
2 . 73
o
SK KH SH
SHK SKH SKH
SK KH
+ −
∆ = = ⇒=
Suy ra:
( ) ( )
( )
; 83,3
o
SAB ABC SKH= =