S PH C VÀ NG D NG S PH C Đ GI I TOÁN V T LÝỐ Ứ Ứ Ụ Ố Ứ Ể Ả Ậ
1) Khái ni mệ :
T p h p các s ph c là t p h p các s th c R và s j sao cho jậ ợ ố ứ ậ ợ ố ự ố 2 = - 1
2) Bi u di n s ph cể ễ ố ứ :
a) D ng đ i sạ ạ ố : z = a + bj v i a, b là các s th c ớ ố ự
a g i là ph n th c; b g i là ph n oọ ầ ự ọ ầ ả
+ N u b = 0 thì z = a là s th cế ố ự
+ N u a = 0 thì z = bj là s thu n oế ố ầ ả
+ z = 0 khi a = b = 0
+ Hai s ph c zố ứ 1 = a1 + b1j và z2 = a2 + b2j b ng nhau khi aằ1 = a2 và b1 = b2
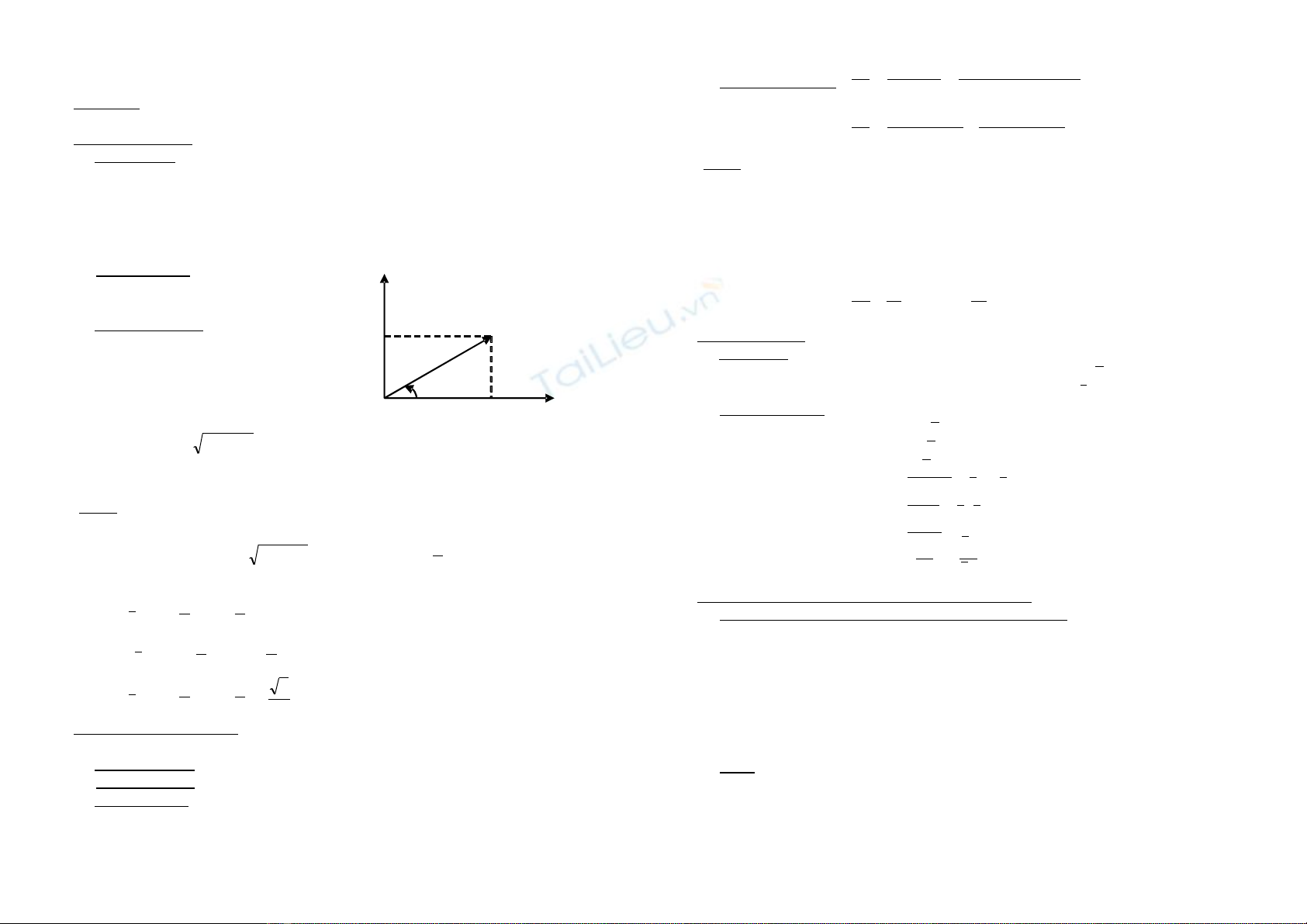
b) D ng hình h cạ ọ :
r OM
=
T a đ c a ọ ộ ủ
r
là a, b
c) D ng l ng giácạ ượ :
a r cos
rb rsin
= ϕ
= ϕ
Suy ra z = a + bj
z = r(cosϕ + jsinϕ)
y(truïc aûo)
b M(z)
r
→
ϕ
O x(truïc thöïc)
a
v i ớr =
22
ba +
Theo công th c Euler ( le) :ứ Ơ cosϕ + jsinϕ = ejϕ
Suy ra : z = rejϕ
Chú ý :
* Có th chuy n m t s ph c t d ng đ i s sang d ng l ng giác ho c d ng reể ể ộ ố ứ ừ ạ ạ ố ạ ượ ặ ạ jϕ;
ho c ng c l i : ặ ượ ạ r =
22 ba +
; tgϕ =
a
b
* M t s tr ng h p riêng :ộ ố ườ ợ
+
= cos
2
π
+ jsin
2
π
= j
+
2
j
e
π
−
= cos(-
2
π
) + jsin(-
2
π
) = - j
+
= cos
4
π
+ jsin
4
π
=
2
2
(1 + j)
3) Các phép tính v i s ph cớ ố ứ :
Cho 2 s ph c :ố ứ z1 = a1 + b1j ; z2 = a2 + b2j
a) T ng 2 s ph cổ ố ứ : z1 + z2 = (a1 + a2) + (b1 + b2)j
b) Hi u 2 s ph cệ ố ứ : z1 - z2 = (a1 - a2) + (b1 - b2)j
c) Tích 2 s ph cố ứ : z1.z2 = (a1 + b1j)(a2 + b2j) = a1a2 + a1b2j + a2b1j - b1b2
V y : ậz1.z2 = (a1a2 - b1b2) + (a1b2 + a2b1)j
d) Th ng 2 s ph cươ ố ứ :
2
2
2
2
2211
22
11
2
1
ba
)jba)(jba(
jba
jba
z
z
+
−+
=
+
+
=
⇔
j
ba
baba
ba
bbaa
z
z
2
2
2
2
1221
2
2
2
2
2121
2
1
+
+−
+
+
+
=
Chú ý :
+ N u bi u di n s ph c d ng l ng giác :ế ể ễ ố ứ ở ạ ượ z1 = r1(cosϕ1 + jsinϕ1)
z2 = r2(cosϕ2 + jsinϕ2)
thì : z1z2 = r1r2[cos(ϕ1 + ϕ2) + jsin(ϕ1 + ϕ2)]
+ N u bi u di n s ph c d ng : ế ể ễ ố ứ ở ạ z1 = r1
1
j
e
ϕ
; z2 = r2
2
j
eϕ
thì : z1z2 = r1r2
)(j 21
eϕ+ϕ
= r1r2[cos(ϕ1 + ϕ2) + jsin(ϕ1 + ϕ2)]
và
2
1
)(j
2
1
2
1
r
r
e
r
r
z
z21 == ϕ−ϕ
[cos(ϕ1 - ϕ2) + jsin(ϕ1 - ϕ2)]
4) S ph c liên h pố ứ ợ :
a) Đ nh nghĩaị :
+ S ph c liên h p c a s ph c z = a + bj là m t s ph c ố ứ ợ ủ ố ứ ộ ố ứ
z
= a - bj
+ S ph c liên h p c a s ph c z = reố ứ ợ ủ ố ứ jϕ là m t s ph c ộ ố ứ
z
= re-jϕ
b) M t s tính ch tộ ố ấ :
* z +
z
= 2a
* z -
z
= 2bj
* z.
z
= a2 + b2
*
1 2
1 2
z z z z =
*
1 2
1 2
z .z z .z=
*
1
1
2
2
zz
zz
� �
=
� �
� �
(z2 ≠ 0)
5) Bi u di n m t dao đ ng đi u hòa b ng m t s ph cể ễ ộ ộ ề ằ ộ ố ứ :
a) Bi u di n m t dao đ ng đi u hòa b ng m t s ph cể ễ ộ ộ ề ằ ộ ố ứ : M t đ i l ng bi n thiênộ ạ ượ ế
đi u hòa theo th i gian x = Acos(ề ờ ωt + ϕ) có th đ c bi u bi n b i m t s ph c ký hi uể ượ ể ễ ở ộ ố ứ ệ
là x*
x* = Aej(ωt + ϕ) = A[cos(ωt + ϕ) + jsin(ωt + ϕ)] = a + bj
v i ph n th c là a = Acos(ớ ầ ự ωt + ϕ) và ph n o là b = Asin(ầ ả ωt + ϕ)
Trong các bài toán dao đ ng đi u hòa, khi t n s góc ộ ề ầ ố ω có tr s xác đ nh thì có thị ố ị ể
bi u di n đ n gi n ể ễ ơ ả x* = Aejϕ = A(cosϕ + jsinϕ) = a + bj
v i ph n th c là a = Acosớ ầ ự ϕ và ph n o là b = Asinầ ả ϕ
b) Ví dụ : Bi u di n b ng s ph c các dao đ ng đi u hòa sau :ể ễ ằ ố ứ ộ ề
+ x = 5cosωt ↔x* = 5ejωt = 5cosωt + j5sinωt
Ho c ặx* = 5 = 5cos0 + j5sin0
Soá phöùc vaø öùng duïng soá phöùc ñeå giaûi toaùn Vaät Lyù Bieân soaïn : GV Phöông Chaùnh Nhôn
1
+ x = 10cos(ωt +
4
π
) ↔x* = 10ej(ωt + π/4)
x* = 10[cos(ωt +
4
π
) + jsin(ωt +
4
π
)
Ho cặx* = 10
= 10(cos
4
π
+ jsin
4
π
)
= 5
(1 + j)
+ x* = 5 + j5 ↔x = 5
cos(ωt +
4
π
)
vì : A =
2555ba 2222 =+=+
và tgϕ =
1
5
5
a
b==
nên ϕ =
4
π
c) T ng h p các dao đ ng đi u hòa cùng t n s b ng s ph cổ ợ ộ ề ầ ố ằ ố ứ :
* Ví d 1ụ : T ng h p hai dao đ ng đi u hòa cùng t n s sau :ổ ợ ộ ề ầ ố
x1 = cos(ωt +
2
π
), x1 = cos(ωt +
6
π
)
Gi iả
Bi u di n b ng s ph c : ể ễ ằ ố ứ x*1 =
= j
x*2 =
= cos
6
π
+ jsin
6
π
=
2
3
+
2
1
j
Dao đ ng t ng h p ộ ổ ợ x* = x*1 + x*2 =
2
3
+
2
3
j
T c là ứx =
3
cos(ωt +
3
π
)
Vì : A =
3
4
9
4
3=+
và tgϕ =
3
2
3
2
3
=
nên ϕ =
3
π
* Ví d 2ụ : T ng h p hai dao đ ng đi u hòa cùng t n s sau :ổ ợ ộ ề ầ ố
x1 = 2cos(πt +
6
π
)(cm); x2 = 2
3
sin(πt +
6
π
)(cm)
Gi iả
Bi n đ i :ế ổ x2 = 2
3
cos(πt -
3
π
)(cm)
Bi u di n b ng s ph c : ể ễ ằ ố ứ
x*1 = 2
= 2(cos
6
π
+ jsin
6
π
) =
3
+ j
x*2 = 2
3
j3
e
π
−
= 2
3
[cos(-
3
π
) + jsin(-
3
π
)] =
3
- 3j
Dao đ ng t ng h p : ộ ổ ợ x* = x*1 + x*2 = 2
3
- 4j
T c là : ứx = 4cos(πt -
2
π
)(cm)
* Ví d 3ụ : T ng h p ba dao đ ng đi u hòa cùng t n s sau : ổ ợ ộ ề ầ ố
x1 = 3cost(cm) ; x2 = 3sint(cm) ; x3 = 7cos(t +
2
π
)(cm)
Gi iả
Bi n đ i :ế ổ x2 = 3cos(t -
2
π
)(cm)
Bi u di n b ng s ph c :ể ễ ằ ố ứ x*1 = 3ej0 = 3
x*2 = 3
j2
e
π
−
= -3j
x*3 = 7
j2
e
π
= 7j
Dao đ ng t ng h p : ộ ổ ợ x* = x*1 + x*2 + x*3 = 3 + 4j
T c : ứx = 5cos(t + ϕ)(cm) vì A =
543 22 =+
V i ớtgϕ =
b 4
a 3
=
* Ví d 4ụ : T ng h p ba dao đ ng đi u hòa sau : xổ ợ ộ ề 1 = 4cos(πt +
6
π
)(cm); x2 =
4cos(πt +
6
5π
)(cm); x3 = 4cos(πt -
2
π
)(cm)
Gi iả
Bi u di n b ng s ph c : ể ễ ằ ố ứ x*1 = 4
= 4(cos
6
π
+ jsin
6
π
) = 2
3
+ 2j
x*2 = 4
6
5
j
e
π
= 4(cos
6
5π
+ jsin
6
5π
) = -2
3
+ 2j
x*3 = 4
2
j
e
π
−
= -4j
Dao đ ng t ng h p :ộ ổ ợ x* = x*1 + x*2 + x*3 = 0
V y ậx = 0
6) V n d ng s ph c đ gi i bài toán đi n xoay chi uậ ụ ố ứ ể ả ệ ề :
a) Ph ng pháp s d ng s ph c đ gi i toán đi n xoay chi uươ ử ụ ố ứ ể ả ệ ề : S d ng tr c dòngử ụ ụ
đi n i làm tr c g c (tr c th c) n m ngang.ệ ụ ố ụ ự ằ
+ Đo n m ch xoay chi u ch có đi n tr thu n Rạ ạ ề ỉ ệ ở ầ :
T ng tr Z = R; góc l ch pha ổ ở ệ ϕ = 0
⇒ T ng tr ph c : Zổ ở ứ * = Rej0 = R
Soá phöùc vaø öùng duïng soá phöùc ñeå giaûi toaùn Vaät Lyù Bieân soaïn : GV Phöông Chaùnh Nhôn
2
+ Đo n m ch xoay chi u ch có cu n thu n c m Lạ ạ ề ỉ ộ ầ ả :
T ng tr Z = Zổ ở L; góc l ch pha ệϕ =
2
π
⇒ T ng tr ph c : Zổ ở ứ * = ZL
= jZL
+ Đo n m ch xoay chi u ch có t đi n Cạ ạ ề ỉ ụ ệ :
T ng tr Z = Zổ ở C : góc l ch pha ệϕ = -
2
π
⇒T ng tr ph c : Zổ ở ứ * = ZL
2
j
e
π
−
= -jZC
+ Đo n m ch n i ti p RLCạ ạ ố ế :
T ng tr ổ ở
2
CL
2)ZZ(RZ −+=
; góc l ch pha ệ
R
ZZ
tg CL −
=ϕ
⇒T ng tr ph c : Zổ ở ứ * = Z
ϕj
e
= R + j(ZL - ZC)
+ Đ nh lu t Ohm d ng ph cị ậ ạ ứ :
*
*
*
Z
U
I=
+ Đo n m ch g m nhi u đo n m ch ghép n i ti pạ ạ ồ ề ạ ạ ố ế :
- T ng tr ph c : ổ ở ứ Z* = Z*1 + Z*2 +...
- Hi u đi n th 2 đ u đo n m ch d ng ph c : Uệ ệ ế ầ ạ ạ ạ ứ * = U*1 + U*2 +...
+ Đo n m ch g m nhi u đo n m ch ghép song songạ ạ ồ ề ạ ạ :
- T ng tr ph c : ổ ở ứ
...
Z
1
Z
1
Z
1
*
2
*
1
*++=
- C ng đ dòng đi n m ch chính d ng ph c : Iườ ộ ệ ạ ạ ứ * = I*1 + I*2 +...
v i ớ
*
1
*
*
1Z
U
I=
;
*
2
*
*
2Z
U
I=
;...
+ Đo n m ch h n h pạ ạ ỗ ợ : Gi i nh bài toán đi n m t chi u v i các giá tr tính toánả ư ệ ộ ề ớ ị
d ng s ph c.ở ạ ố ứ
+ Công th c chuy n đ i t m ch tam giác (ứ ể ổ ừ ạ
∆
) sang m ch sao (Y) d ng s ph cạ ở ạ ố ứ :
A
B
C
Z
*12
Z
*23
Z
*13
A
B
C
Z
*1
Z
*2
Z
*3
⇔
* * * *
* *
* * *
2 3 1 3
1 2
12 23 13
* * * * * * * * *
1 2 3 1 2 3 1 2 3
Z Z Z Z
Z Z
Z ; Z ; Z
Z Z Z Z Z Z Z Z Z
= = =
+ + + + + +
b) Ví dụ :
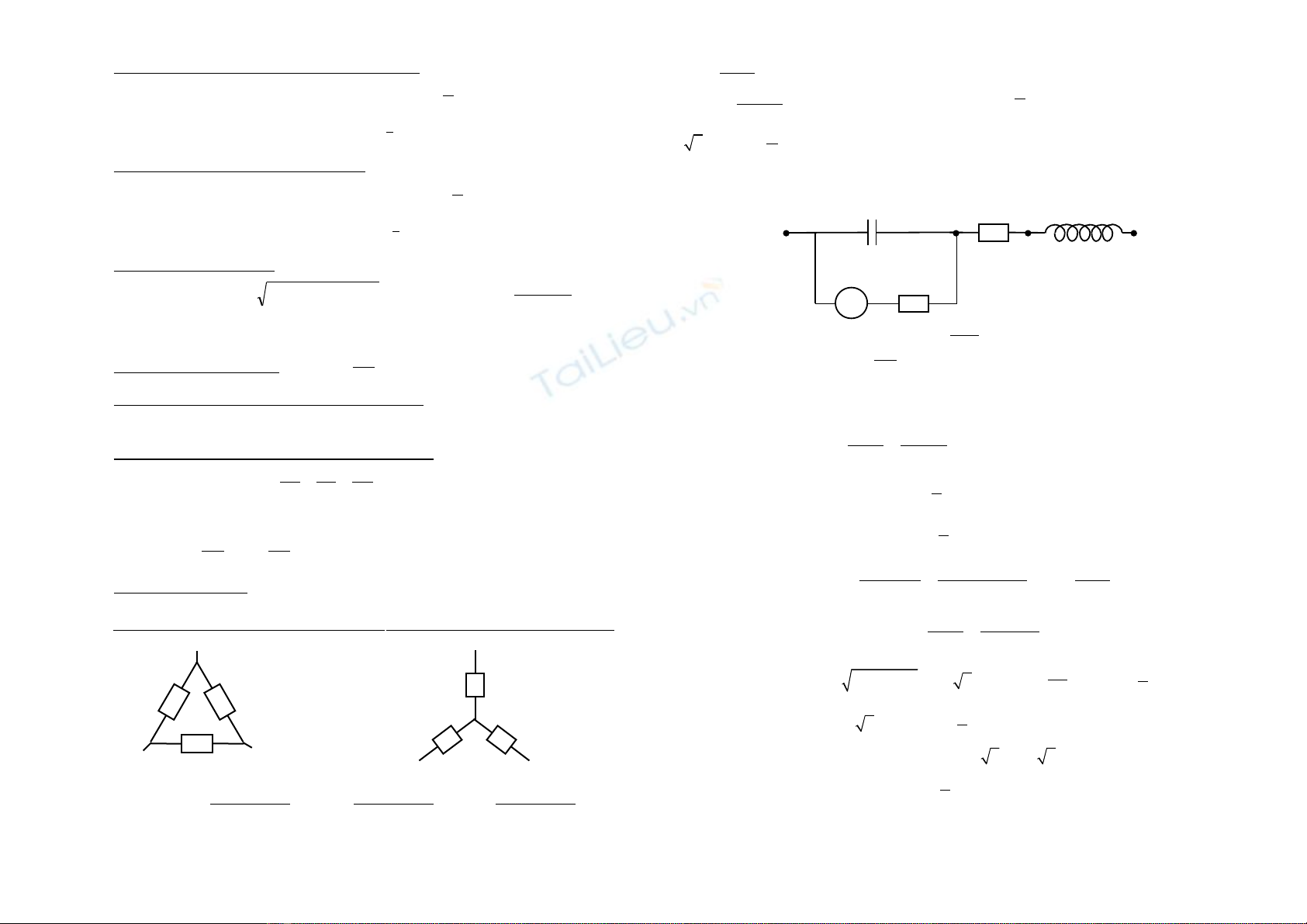
* Ví d 1ụ : Cho m ch đi n nh hình v : C = ạ ệ ư ẽ
1
π
.10-5F; R1 = 1kΩ; R2 = 282Ω ≈ 200
2
Ω; L =
5
π
H; RA ≈ 0. C ng đ dòng đi n qua ampère k có bi u th c iườ ộ ệ ế ể ứ A =
0,1cos100πt(A). Tìm bi u th c c ng đ dòng đi n qua C và qua Rể ứ ườ ộ ệ 2, các bi u th c hi uể ứ ệ
đi n th uệ ế DE, uEB, uAB.
A C D R
2
E L B
R
1
A
Gi iả
ZL = ωL = 500Ω; ZC =
1
Cω
= 1000Ω
Bi u di n b ng s ph c : Zể ễ ằ ố ứ *L = 500j ; Z*C = - 1000j ; R*1 = 1000Ω ; I*A = 0,1A
⇒U*AD = I*AR*1 = 100V
I*C =
*
AD
*
C
U100 0,1j
1000j
Z= =
−
⇒IoC = 0,1A và ϕic =
2
π
⇒iC = 0,1cos(100πt +
2
π
)(A)
Z*AD =
* *
C 1
* *
C 1
Z .R 1000j.1000 j
1000 500(1 j)
1000j 1000 j 1
Z R
− −
= = = −
− + − +
+
Dòng đi n m ch chính : Iệ ạ * = I*R2 =
*
AD
*
AD
U100 0,1(1 j)
500(1 j)
Z= = +
−
⇒Io =
2 2
0,1 0,1 0,1 2+ =
A ; tanϕi =
= 1 ; ϕi =
4
π
⇒i = 0,1
2
cos(100πt +
4
π
)(A)
U*DE = I*R*2 = 0,1(1+j).200
2
= 20
2
(1 + j)
⇒UoDE = 40V ; ϕuDE =
4
π
Soá phöùc vaø öùng duïng soá phöùc ñeå giaûi toaùn Vaät Lyù Bieân soaïn : GV Phöông Chaùnh Nhôn
3
⇒uDE = 40cos(100πt +
4
π
)(V)
U*EB = I*Z*L = 0,1(1 + j).500j = 50(j - 1)
⇒uEB = 50
2
cos(100πt -
4
π
)(V)
U*AB = U*AD + U*DE + U*EB = 100 + 20
2
(1 + j) + 50(j - 1)
= (50 + 20
2
)(1 + j)
⇒uAB = (50 + 20
2
)
2
cos(100πt +
4
π
)(V)
* Ví d 2ụ : Cho m ch đi n nh hình v : R = 50ạ ệ ư ẽ Ω; L =
1
2π
H; uAB = Uocos(100πt).
Tìm giá tr c a C đ dòng đi n m ch chính cùng pha v i uị ủ ể ệ ạ ớ AB.
C
A B
L R
Gi iả
Ta có : Z*C = -jZC ; Z*L = jZL = 50j ; R* = R = 50 ; U* = Uo
Z*1 = Z*L + R* = 50 + 50j
Z* =
* *
C 1 C
* * C
C 1
Z Z 50Z ( j 1)
50 j(50 Z )
Z Z
−
=+ −
+
=
C C C
2 2
C
50Z (100 Z ) j Z
50 (50 Z )
− −
+ −
Đ i cùng pha u thì ểϕ = 0 ⇔100 - ZC = 0
⇒ZC = 100Ω
⇒C =
4
10−
π
F
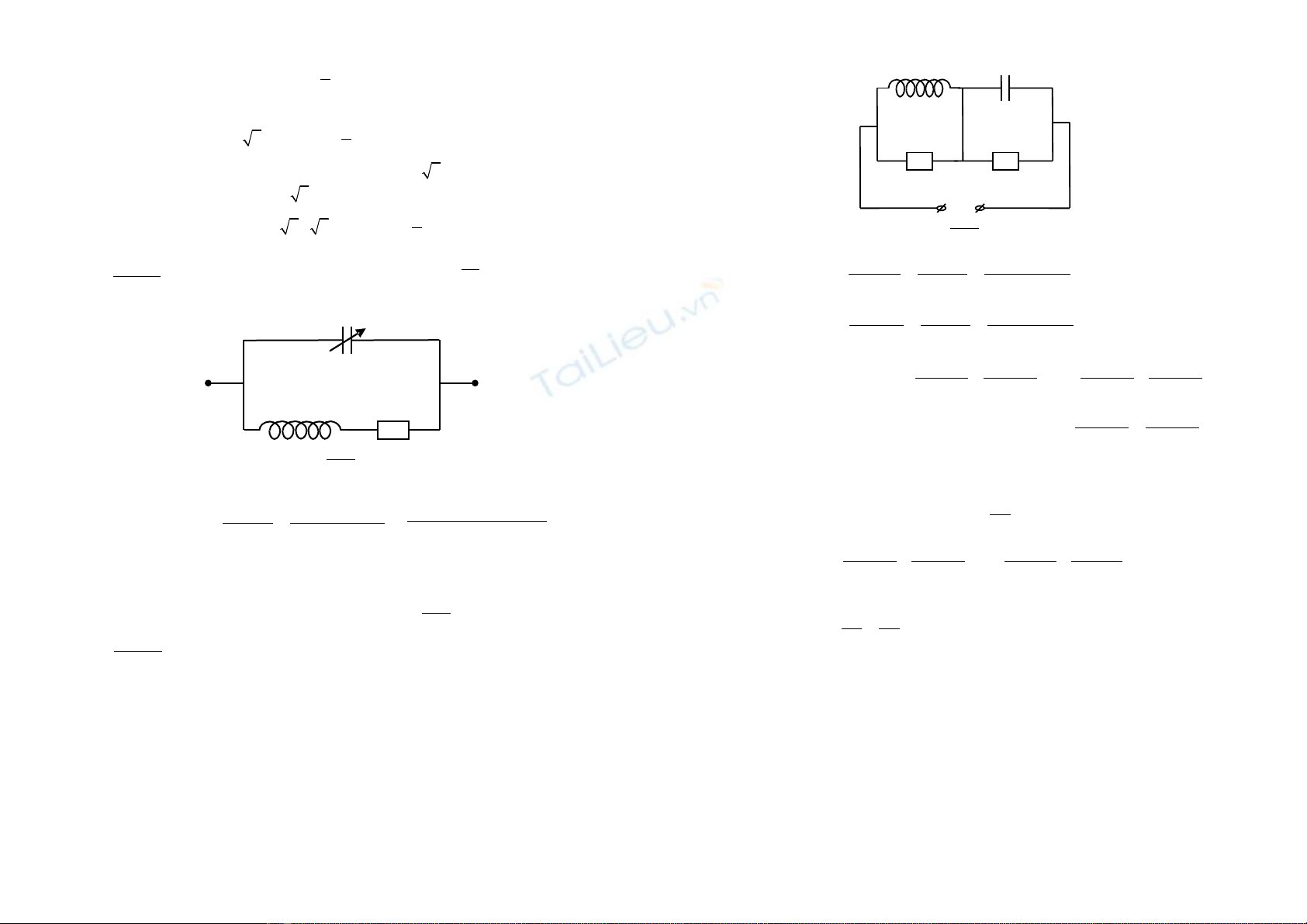
* Ví d 3ụ : Cho m ch đi n nh hình v : Rạ ệ ư ẽ 1 = R2 = R = 10Ω; L = 0,2.10-3H; gi aữ
hai đ u A và B đ t m t hi u đi n th u = 110sin100ầ ặ ộ ệ ệ ế πt(V). Cu n dây c m thu n. ộ ả ầ
1) H i t đi n ph i có đi n dung C b ng bao nhiêu đ dòng đi n trong m chỏ ụ ệ ả ệ ằ ể ệ ạ
chính cùng pha v i hi u đi n th u m i t n s .ớ ệ ệ ế ở ọ ầ ố
2) Tính c ng đ dòng đi n c c đ i m ch chính lúc đó.ườ ộ ệ ự ạ ở ạ
L M C
I
L
I
C
A B
I
1
I
2
I
o
R
1
N R
2
~
Gi iả
1) Ta có : Z*L = jZL ; Z*C = -jZC ; R*1 = R*2 = R ; U* = 110
2 2
* *
*C L
L 1 L
1* * 2 2
L
L 1 L
RZ R Z j
Z R RZ j
ZR Z j
Z R R Z
+
= = =
+
+ +
* * 2 2
*C 2 C C C
2* * 2 2
C
C 2 C
Z R RZ j RZ R Z j
ZR Z j
Z R R Z
− −
= = =
−
+ +
Z* = Z*1 + Z*2 =
2
2
2
C C
L L
2 2 2 2 2 2 2 2
L C L C
RZ Z
RZ Z
R j
R Z R Z R Z R Z
� �
+ + −
� �
� �
+ + + +
� �
i và u cùng pha khi ϕ = 0 , t c là : ứ
C
L
2 2 2 2
L C
Z
Z
R Z R Z
=
+ +
⇔(ZL - ZC)(R2 - ZLZC) = 0
⇔ZLZC = R2
⇔C =
2
L
R
2) T ng tr : Zổ ở * =
2
2
C
L
2 2 2 2
L C
RZ
RZ
R Z R Z
+
+ +
= R
22
L
2 2 2 2
L L
ZR
R Z R Z
� �
+
� �
+ +
� �
= R
⇒Z = R
⇒Io =
o o
U U
Z R
=
= 11A
Soá phöùc vaø öùng duïng soá phöùc ñeå giaûi toaùn Vaät Lyù Bieân soaïn : GV Phöông Chaùnh Nhôn
4