6
Node-Pair Encoding Genetic
Programming for Optical Mesh
Network Topology Design
Mark C. Sinclair
6.1 Introduction
Telecommunications is a vital and growing area, important not only in its own right, but
also for the service it provides to other areas of human endeavour. Moreover, there
currently seems to be a demand for an ever-expanding set of telecommunication services of
ever-increasing bandwidth. One particular technology that has the potential to provide the
huge bandwidths necessary if such broadband services are to be widely adopted, is multi-
wavelength all-optical transport networks (Mukherjee, 1997). However, the development of
such networks presents scientists and engineers with a challenging range of difficult design
and optimisation problems.
One such problem is mesh network topology design. In the general case, this starts with
a set of node locations and a traffic matrix, and determines which of the node pairs are to be
directly connected by a link. The design is guided by an objective function, often cost-
based, which allows the ‘fitness’ of candidate networks to be evaluated. In the more specific
problem of the topology design of multi-wavelength all-optical transport networks, the
nodes would be optical cross-connects, the links optical fibres, and the traffic static.
Suitable routing and dimensioning algorithms must be selected, with sufficient allowance
for restoration paths, to ensure that the network would at least survive the failure of any
single component (node or link).
Telecommunications Optimization: Heuristic and Adaptive Techniques, edited by D.W. Corne, M.J. Oates and G.D. Smith
© 2000 John Wiley & Sons, Ltd
Telecommunications Optimization: Heuristic and Adaptive Techniques.
Edited by David W. Corne, Martin J. Oates, George D. Smith
Copyright © 2000 John Wiley & Sons Ltd
ISBNs: 0-471-98855-3 (Hardback); 0-470-84163X (Electronic)
100 Telecommunications Optimization: Heuristic and Adaptive Techniques
In previous work, Sinclair (1995; 1997) has applied a simple bit-string Genetic
Algorithm (GA), a hybrid GA and, with Aiyarak and Saket (1997) three different Genetic
Programming (GP) approaches to this problem. In this chapter, a new GP approach,
inspired by edge encoding (Luke and Spector, 1996), is described (a shorter version of this
chapter was first published at GECCO’99 (Sinclair, 1999)). It was hoped that this would
provide better results than the best previous GP approach, and perhaps even prove
competitive with GAs. The eventual aim of the author’s current research into GP encoding
schemes for mesh network topologies is to provide a more scalable approach than the
inherently non-scalable encoding provided by bit-string GAs.
The chapter is structured as follows. Section 6.2 presents some of the previous work on
Evolutionary Computation (EC) for network topology design; section 6.3 provides a more
detailed description of the problem tackled, including the network cost model; and section
6.4 summarises two previous solution attempts. In section 6.5 the node-pair encoding GP
approach is described; then in section 6.6 some experimental results are outlined; and
finally, section 6.7 records both conclusions and suggestions for further work.
6.2 EC for Network Topology Design
Over the years, at least 30 papers have been published on EC approaches to network
topology design. Two of the earliest are by Michalewicz (1991) and Kumar et al. (1992).
Michalewicz uses a two-dimensional binary adjacency matrix representation, and problem-
specific versions of mutation and crossover, to evolve minimum spanning tree topologies
for computer networks. Kumar et al. tackle three constrained computer network topology
problems, aiming for maximum reliability, minimum network diameter or minimum
average hop count. Their GA is bit-string, but uses problem-specific crossover, as well as a
repair operator to correct for redundancy in their network representation.
For optical network topology design, in addition to the papers by Sinclair, mentioned
above, there is the work of Paul et al. (1996) and Brittain et al. (1997). Both these groups of
authors have addressed constrained minimum-cost Passive Optical Network (PON)
topology design for local access. However, while problem-specific representations are used
by both, as well as problem-specific genetic operators by Paul et al., only Brittain et al.
provide full details of their algorithm. This uses a two-part chromosome comprising a bit-
string and a permutation, with each part manipulated with appropriate standard operators.
Other recent work of interest includes Dengiz et al. (1997; Chapter 1, this volume) on a
hybrid GA for maximum all-terminal network reliability, Ko et al. (1997a), who use a
three-stage GA for computer network topology design, routing and capacity assignment;
and Pierre and Legault (1998), who use a bit-string GA for computer mesh network design.
6.3 Problem Description
Given the locations of the n nodes (optical cross connects) and the static traffic
requirements, ,
ij
tbetween them, the problem is to determine which of the n(n–1)/2 possible
bi-directional links (optical fibres) should be used to construct the network. The number of
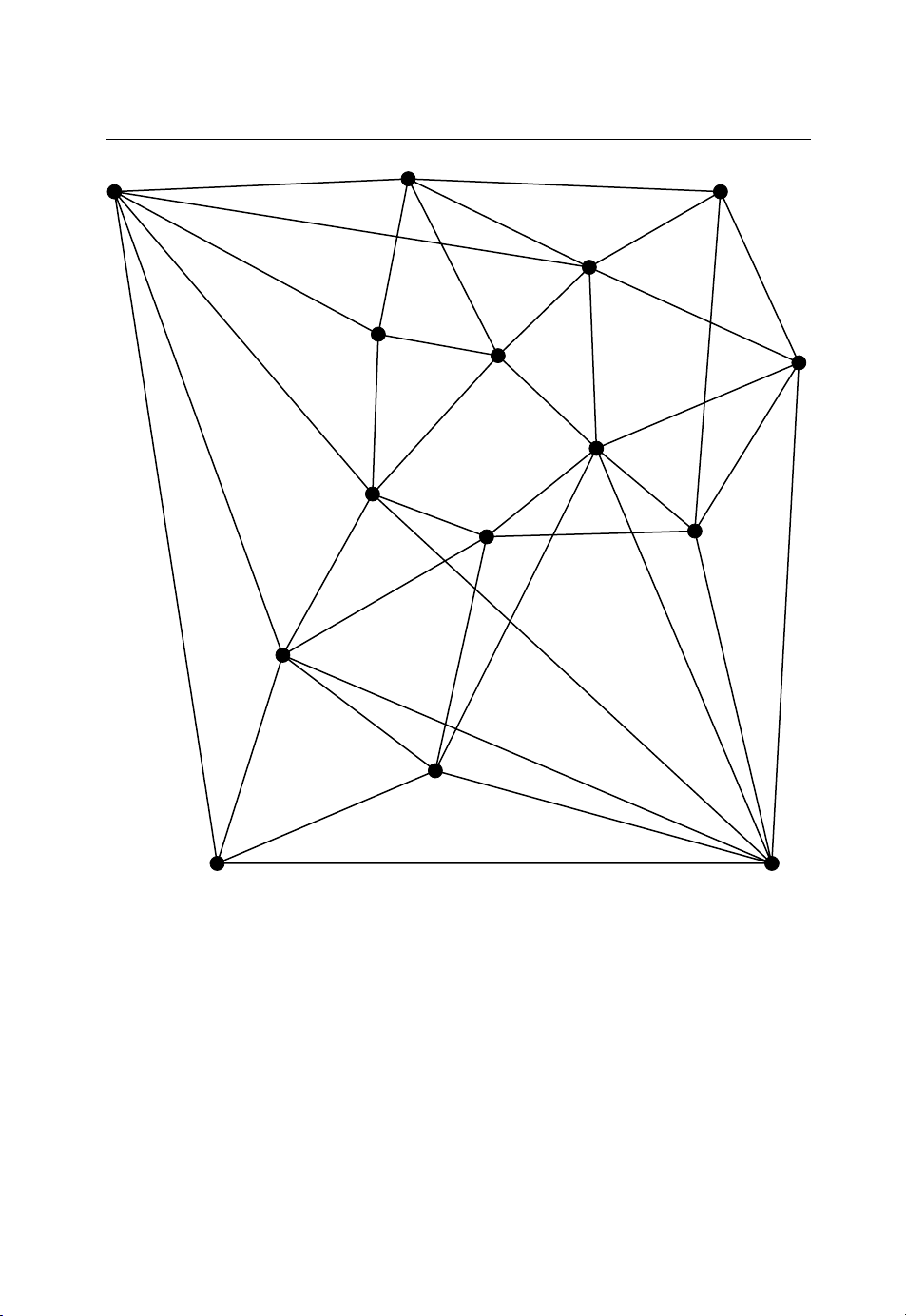
possible topologies is thus .2 2/)1( −nn To illustrate, Figure 6.1 shows a 15-node network
design problem, for which an example mesh topology design is given in Figure 6.2.
Node-Pair Encoding Genetic Programming for Optical Mesh Network Topology Design 101
Figure 6.1 Example network design problem.
The cost model used to guide the design was developed by Sinclair (1995) for
minimum-cost topology design of the European Optical Network (EON) as part of the
COST 239 initiative (O’Mahony et al., 1993). It assumes static two-shortest-node-disjoint-
path routing (Chen, 1990) between node pairs, and that a reliability constraint is used. This
is to ensure that there are two, usually fully-resourced, node-disjoint routes between node
pairs, thus guaranteeing the network will survive the failure of any single component.
To determine the cost of a given topology, separate models for both links and nodes are
required. The intention is to approximate the relative contribution to purchase, installation
and maintenance costs of the different network elements, while ensuring the model is not
too dependent on the details of the element designs, nor too complex for use in the ‘inner
loop’ of a design procedure.
102 Telecommunications Optimization: Heuristic and Adaptive Techniques
Figure 6.2 Example mesh topology.
First, the two-shortest-node-disjoint routes are determined for all node pairs. In this, the
‘length’ of each path is taken to be the sum of the contributing link weights, with the weight
of the bi-directional link between nodes i and j given by:
jijiij NLNW 5.05.0 ++= (6.1)
where Ni and Nj are the node effective distances of nodes i and j, respectively (see below)
and Lij is the length of link (i,j) in km. Then, the link carried traffic is determined for each
link by summing the contributions from all the primary and restoration routes that make use
of it. The restoration traffic is weighted by a parameter KR, but restoration routes are
usually taken to be fully-resourced (i.e. KR = 1.0), and thus are assumed to carry the same
Node-Pair Encoding Genetic Programming for Optical Mesh Network Topology Design 103
traffic as the corresponding primary routes, i.e. the traffic they would be required to carry if
their primary route failed. The capacity of link (i,j) is taken to be:
)(ceil ijTKij TKV G
=(6.2)
where Tij is the carried traffic in Gbit/s on the link, and ceilx() rounds its argument up to the
nearest x – here, the assumed granularity of the transmission links, KG (say 2.5 Gbit/s). The
factor of KT (say 1.4) is to allow for stochastic effects in the traffic. The cost of link (i,j) is
then given by:
ij
ij
ij LVC
α
=(6.3)
where
α
is a constant (here taken to be 1.0). Increasing capacity necessarily implies
increased cost due, for example, to wider transmission bandwidth, narrower wavelength
separation and/or increasing number and speed of transmitters and receivers. With
α
= 1, a
linear dependence of cost on capacity is assumed, but with
α
< 1, the cost can be adjusted
to rise more slowly with increases in the link capacity. The linear link length dependency
approximates the increasing costs of, for example, duct installation, fibre blowing and/or
the larger number of optical amplifiers with increasing distance.
Node effective distance was used as a way of representing the cost of nodes in an
optical network in equivalent distance terms. It can be regarded as the effective distance
added to a path as a result of traversing a node. By including it in link weights (equation
6.1) for the calculation of shortest paths, path weights reflect the cost of the nodes traversed
(and half the costs of the end nodes). As a result, a longer geographical path may have a
lower weight if it traverses fewer nodes, thereby reflecting the relatively high costs of
optical switching. The node effective distance of node i was taken to be:
nii KnKN += 0(6.4)
where ni is the degree of node i, i.e. the number of bi-directional links attached to it. The
constants K0 and Kn were taken to be, say 200 km and 100 km, respectively, as these were
judged to be reasonable for the network diameters of 1400–3000 km used here. Node
effective distance thus increases as the switch grows more complex. Node capacity is the
sum of the capacities of all the attached links, i.e.
∑
=
j
iji VV (6.5)
where Vi is the capacity of node i in Gbit/s. The node cost was taken to be:
iii VNC 5.0=(6.6)
The cost is thus derived as if the node were a star of links, each of half the node effective
length, and each having the same capacity as the node itself. Further, if all the links