GV. TRÖÔNG ÑÌNH HUØNG ÑT: 0908.346.838 Trang 1
TRUNG TAÂM LUYEÄN THI ÑAÏI HOÏC ÑAÏI VIEÄT ( NGUYEÂN LAØ TTLT ÑAÏI HOÏC SÖ PHAÏM TP.HCM )
TÓM TẮT CÔNG THỨC VÀ LÝ THUYẾT VẬT LÝ 12-LUYỆN THI
ĐẠI HỌC VÀ CAO ĐẲNG
ÑOÄNG LÖÏC HOÏC VAÄT RAÉN
1. Chuyeån ñoäng quay ñeàu:
Tốc độ góc trung bình ωtb của vật rắn là : t
tb Δ
Δ
=
ϕ
ω
Tốc độ góc tức thời ω: t
tΔ
Δ
=→Δ
ϕ
ω
0
lim hay )(
't
ϕω
=
Vaän toác goùc
ω
= haèng soá.
Toaï ñoä goùc. t
ω
ϕ
ϕ
+= 0
Vaän toác daøi cuûa ñieåm caùch taâm quay khoaûng r :
r
v
×
=
ω
2. Chuyeån ñoäng quay bieán ñoåi ñeàu:
Gia tốc góc trung bình γtb: t
tb Δ
Δ
=
ω
γ
Gia tốc góc tức thời γ: t
tΔ
Δ
=→Δ
ω
γ
0
lim hay )(
't
ωγ
=
Gia toác goùc:
γ
= haèng soá.
Vaän toác goùc: t
γ
ω
ω
+= 0
Toaï ñoä goùc: 2
2
1
00 tt
γωϕϕ
++=
Coâng thöùc ñoäc laäp vôùi thôøi gian: )(2 0
2
0
2
ϕϕγωω
−=−
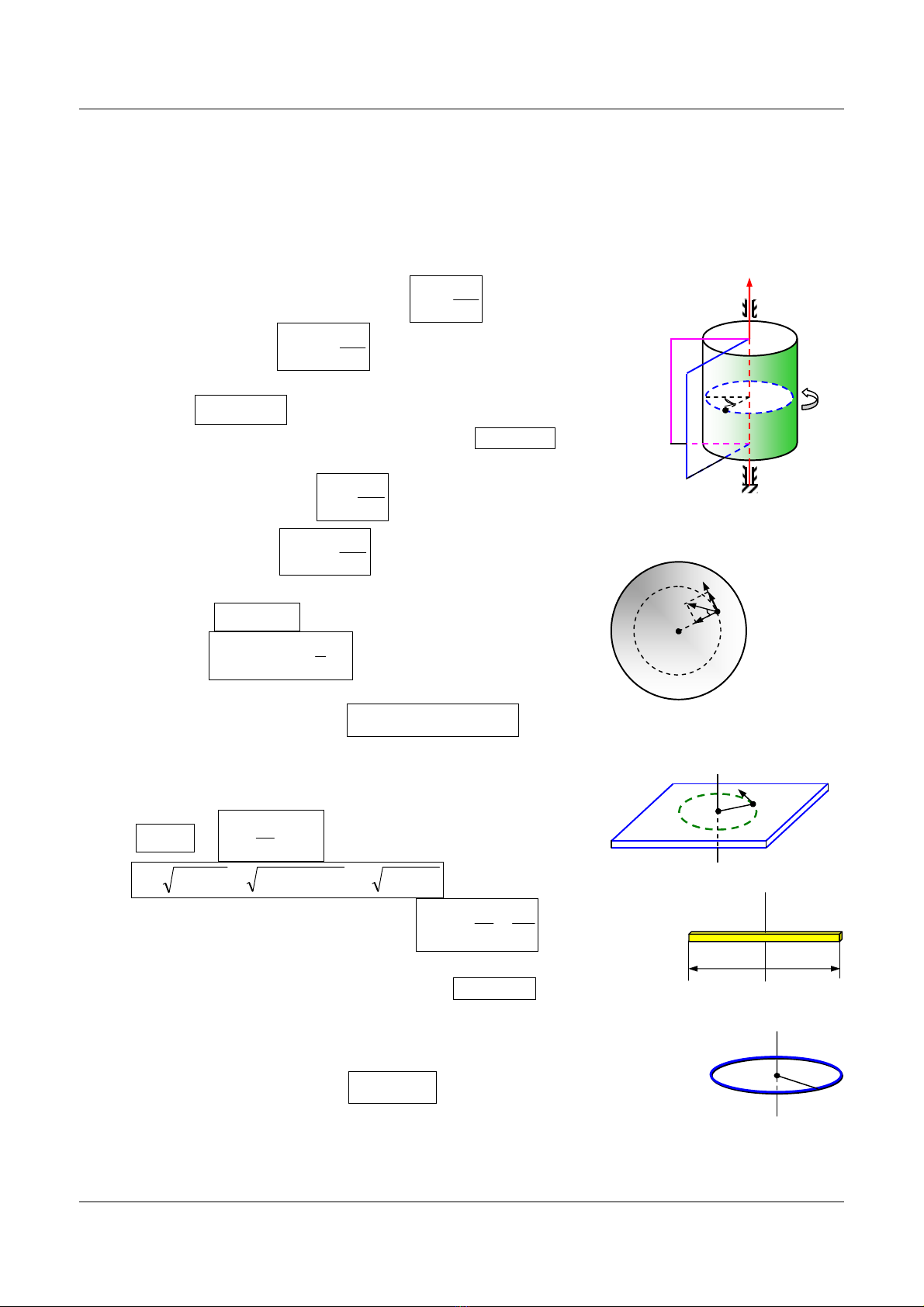
3. Lieân heä giöõa vaän toác daøi, gia toác cuûa moät ñieåm treân vaät raén
vôùi vaän toác goùc, gia toác goùc:
γ
rat= ; r
r
v
an
2
2
ω
== ;
42422222
ωγωγ
+=+=+= rrraaa tn
Vectô gia toác a
r hôïp vôùi kính goùc
α
vôùi: 2
tan
ω
γ
α
==
n
t
a
a
4. Momem:
a. Momen löïc ñoái vôùi moät truïc quay coá ñònh: dFM
×
=
F laø löïc taùc duïng;
d laø caùnh tay ñoøn (ñöôøng thaúng haï töø taâm quay vuoâng goùc vôùi phöông cuûa löïc
b. Momen quaùn tính ñoái vôùi truïc:
∑
=2
iirmI (kg.m2)
Vôùi : m laø khoái löôïng,
r laø khoaûng caùch töø vaät ñeán truïc quay
P0
P
A
z
Hình
φ
r
O
v
r
t
a
r
n
a
r
a
r
r
O
M
α
Hình 2
O
r
F
r
Δ
Δ
L
R
Δ
Hình
www.MATHVN.com
WWW.MATHVN.COM

GV. TRÖÔNG ÑÌNH HUØNG ÑT: 0908.346.838 Trang 2
TRUNG TAÂM LUYEÄN THI ÑAÏI HOÏC ÑAÏI VIEÄT ( NGUYEÂN LAØ TTLT ÑAÏI HOÏC SÖ PHAÏM TP.HCM )
* Momen quaùn tính cuûa thanh coù tieát dieän nhoû so vôùi chieàu daøi vôùi truïc qua trung ñieåm:
2
12
1mLI =
* Momen quaùn tính cuûa vaønh troøn baùn kính R truïc quay qua taâm:
2
mRI =
* Momen quaùn tính cuûa ñóa ñaëc deït truïc quay qua taâm:
2
2
1mRI =
* Momen quaùn tính cuûa quaû caàu ñaëc truïc quay qua taâm:
2
5
2mRI =
b. Momen ñoäng löôïng ñoái vôùi moät truïc:
ω
IL = (kg.m/s)
c. Moâmen quaùn tính cuûa vaät ñoái vôùi truïc
Δ
song song vaø caùch truïc qua taâm G ñoaïn d .
2
mdII G+=
Δ
5. Hai daïng phöông trình ñoäng löïc hoïc cuûa vaät raén quay quanh moät truïc coá ñònh:
γ
IM = vaø dt
dL
M=
6. Ñònh luïaât baûo toaøn ñoäng löôïng:
Neáu M = 0 thì L = haèng soá
AÙp duïng cho heä vaät : 21 LL += haèng soá
AÙp duïng cho vaät coù momen quaùn tính thay ñoåi: 2211
ω
ω
II
=
7. Động năng của vật rắn quay quanh một trục cố định
Động năng Wđ của vật rắn quay quanh một trục cố định là : 2
2
1
ω
IWđ=
trong đó: I là momen quán tính của vật rắn đối với trục quay
ω là tốc độ góc của vật rắn trong chuyển động quay quanh trục
Động năng Wđ của vật rắn quay quanh một trục cố định có thể viết dưới dạng : WđI
L
2
2
=
trong đó : L là momen động lượng của vật rắn đối với trục quay
I là momen quán tính của vật rắn đối với trục quay
Động năng của vật rắn có đơn vị là jun, kí hiệu là J.
8. Định lí biến thiên động năng của vật rắn quay quanh một trục cố định
Độ biến thiên động năng của một vật bằng tổng công của các ngoại lực tác dụng vào vật.
ΔWđ = AII =− 2
1
2
22
1
2
1
ωω
trong đó : I là momen quán tính của vật rắn đối với trục quay
1
ω
là tốc độ góc lúc đầu của vật rắn
2
ω
là tốc độ góc lúc sau của vật rắn
A là tổng công của các ngoại lực tác dụng vào vật rắn
ΔWđ là độ biến thiên động năng của vật rắn
9. Ñoäng naêng cuûa vaät raén chuyeån ñoäng song phaúng:
Δ
R
Hình
Δ
R
Hình
www.MATHVN.com
WWW.MATHVN.COM

GV. TRÖÔNG ÑÌNH HUØNG ÑT: 0908.346.838 Trang 3
TRUNG TAÂM LUYEÄN THI ÑAÏI HOÏC ÑAÏI VIEÄT ( NGUYEÂN LAØ TTLT ÑAÏI HOÏC SÖ PHAÏM TP.HCM )
22
2
1
2
1
CđmvIW +=
ω
m laø khoái löôïng cuûa vaät, vC laø vaän toác khoái taâm
DAO ÑOÄNG ÑIEÀU HOAØ - CON LAÉC LOØ XO
I. Dao ñoäng ñieàu hoøa:
Dao ñoäng ñieàu hoaø laø dao ñoäng maø traïng thaùi dao ñoäng ñöôïc moâ taû baèng ñònh luaät daïng sin( hoaëc
cosin) ñoái vôùi thôøi gian .
1. Phöông trình dao ñoäng (phöông trình li ñoä)
)cos(
ϕ
ω
+= tAx
trong ñoù :
A,
ω
,φ laø nhöõng haèng soá.
A [m] laø bieân ñoä ;
ω
[rad/s] laø taàn soá goùc
ϕ
[rad] laø pha ban ñaàu
ϕ
ω
+t [rad] pha dao ñoäng
Giá trị đại số của li độ: AxCĐ=; AxCT
−
=
Độ lớn: |x|max =A (vị trí biên) ; |x|min =0 (vị trí cân bằng)
2. Vaän toác: )sin(
ϕ
ω
ω
+−= tAv (m)
Giá trị đại số của vận tốc:
AvCĐ
ω
= VTCB theo chieàu döông ; AvCT
ω
−
=
VTCB theo chieàu aâm
Độ lớn vân tốc :
Av
ω
=
max (vị trí cân bằng ) ; 0
min
=
v ( ôû hai bieân )
Chuù yù: vaät ñi theo chieàu döông v>0, theo chieàu aâm v<0.
Tốc độ là giá trị tuyệt đối của vận tốc
3. Gia toác: xtAa 22 )cos(
ωϕωω
−=+−= (m/s2)
Giá trị đại số của gia tốc:
* AaCĐ
2
ω
= vò trí bieân aâm * AaCT
2
ω
−= vò trí bieân döông
Độ lớn gia tốc:
* Aa 2
max
ω
= vị trí biên ; * 0
min
=
a vò trí caân baèng
Chuù yù: a
r
luoân höôùng veà vò trí caân baèng
4. Coâng thöùc ñoäc laäp: 2
2
22
ω
v
xA += => 22 xAv −±=
ω
; 2
2
4
2
2va
Aω
+
ω
=
5. Taàn soá goùc – chu kyø – taàn soá:
m
k
=
ω
; ;2
2
k
m
T
π
ω
π
== hoaëc N
t
T= ; t laø thôøi gian thöïc hieän N laàn dao ñoäng.
m
k
f
ππ
ω
2
1
2== ; hoaëc T
f1
=
2
1
2
2
1
2
2
1
2
2
2
1
1
1
2
2
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⇒
⎪
⎪
⎭
⎪
⎪
⎬
⎫
==
==
N
N
m
m
T
T
k
m
N
t
T
k
m
N
t
T
π
π
6. Moái lieân heä giöõa li ñoä, vaän toác, gia toác:
)cos(
ϕ
ω
+= tAx ;
→
P
→
ñh
F
→
N →
F
O
x
l0
→
ñh
F
→
P
O
(+)
Δl
www.MATHVN.com
WWW.MATHVN.COM

GV. TRÖÔNG ÑÌNH HUØNG ÑT: 0908.346.838 Trang 4
TRUNG TAÂM LUYEÄN THI ÑAÏI HOÏC ÑAÏI VIEÄT ( NGUYEÂN LAØ TTLT ÑAÏI HOÏC SÖ PHAÏM TP.HCM )
)
2
cos()
2
cos()sin()sin(
π
ϕωω
π
πϕωωπϕωωϕωω
++=−++=++=+−= tAtAtAtAv
)cos()cos( 22
πϕωωϕωω
++=+−= tAtAa
** Vaän toác nhanh pha hôn li ñoä goùc 2
π
** Gia toác nhanh pha hôn vaän toác goùc 2
π
** Gia toác nhanh pha hôn li ñoä goùc
π
7. Naêng löôïng dao ñoäng
* Ñoäng naêng: )(sin
2
1
2
12222
ϕωω
+== tAmmvWđ
* Theá naêng : )(cos
2
1
2
1222
ϕω
+== tKAKxWt Vôùi: 2
ω
mk =
* Cô naêng: W = Wñ + Wt = 2
1kA 2 = 2
1mω2A 2 = Wñ max = Wt max = Const
löu yù:
Con laéc dao ñoäng vôùi chu kyø T, taàn soá f ,taàn soá goùc
ω
thì theá naêng, ñoäng naêng dao ñoäng vôùi
chu
Kyø 2/T, taàn soá 2f, taàn soá goùc
ω
2. Coøn cô naêng luoân khoâng ñoåi theo thôøi gian.
* Động năng và thế năng trung bình trong thời gian nT/2 ( n∈N*, T là chu kỳ dao động) là:
22
W1
24
mA
ω
=
* Tại vị trí có Wđ = nWt ta có:
+ Toạ độ: (n + 1). 2
1kx2 = 2
1kA2 <=> x = ± 1n
A
+
+ Vận tốc: n
1n +.2
1mv2 = 2
1mω2A2 <=> v = ± ωA1n
n
+
* Tại vị trí có Wt = nWđ ta có:
+ Toạ độ: n
1n +.2
1kx2 = 2
1kA2 <=> x = ± A 1+n
n
+ Vận tốc: (n + 1). 2
1mv2 = 2
1mω2A2 <=> v = ± 1n
A
+
ω
8. Löïc phuïc hoài: Laø löïc ñöa vaät veà vò trí caân baèng(löïc ñieàu hoaø),
luoân höôùng veà vò trí caân baèng
xkF r
r−= ; Ñoä lôùn xkF =
Taïi VTCB: 0
min
=
F ; Taïi vi trí bieân : kAF
=
max
9. Löïc ñaøn hoài: laø löïc ñöa vaät veà vò trí chieàu daøi töï nhieân 0
l
Taïi vò trí coù li ñoä x:
xlkFđh±Δ= Vôùi 0
lll −=Δ
* Con laéc coù loø xo naèm ngang: 0
=
Δ
l do ñoù phđhFF
=
* Con laéc coù loø xo thaúng ñöùng: lkmg
Δ
=
α = 300
→
P
→
P’
→
P’’
α
α = 300
→
P
→
N
→
P’’
α
→
ñh
F
x
O
l0
→
ñh
F
→
P
O
(+)
Δl
www.MATHVN.com
WWW.MATHVN.COM

GV. TRÖÔNG ÑÌNH HUØNG ÑT: 0908.346.838 Trang 5
TRUNG TAÂM LUYEÄN THI ÑAÏI HOÏC ÑAÏI VIEÄT ( NGUYEÂN LAØ TTLT ÑAÏI HOÏC SÖ PHAÏM TP.HCM )
+ Chieàu döông thaúng ñöùng höôùng xuoáng: xlkFđh+Δ=
+ Chieàu döông thaúng ñöùng höôùng leân : xlkFđh−Δ=
* Con laéc naèm treân maët phaúng nghieâng moät goùc
α
so vôùi maët phaúng ngang:
+ lkmg Δ
=
α
sin
+ Chieàu döông höôùng xuoáng: xlkFđh+Δ=
+ Chieàu döông höôùng leân : xlkFđh−Δ=
Löïc ñaøn hoài cöïc ñaïi: )(
max_ AlkFđh
+
Δ
=
Löïc ñaøn hoài cöïc tieåu:
Neáu A≥ ∆l : Fñh min = 0 (ÔÛ vò trí loø xo coù chieàu daøi töï nhieân: Fñh = 0)
Neáu A < ∆l : )(
min_ AlkFđh
−
Δ
=
10. Chieàu daøi töï nhieân lo , chieàu daøi cöïc ñaïi lmax , chieàu daøi cöïc tieåu lmin
ÔÛ vò trí loø xo coù chieàu daøi töï nhieân: Fñh = 0
* lllcb Δ+= 0 (taïi vò trí caân baèng loø xo bò daõn)
* lllcb Δ−= 0 (taïi vò trí caân baèng loø xo bò neùn)
* All cb +=
max
* All cb −=
min
* 22
minmax MNll
A=
−
=, vôùi MN = chieàu daøi quyõ ñaïo =2A
* 2
minmax ll
lcb
+
=
11. Con laéc loø xo goàm n loø xo:
Maéc noái tieáp: * ñoä cöùng
nnt kkkk
1
...
111
21
+++=
* chu kyø Tnt = 2
nt
k
m
π
vaø 22
2
2
1
2... nnt TTTT +++=
Maéc song song: * ñoä cöùng n
kkkkk
+
+
+
+
=
...
321//
* chu kyø T// = 2
π
//
k
mvaø 22
2
2
1
2
//
1111
n
TTTT +++= K
Con laéc loø xo khi treo vaät coù khoái löôïng m1 thì chu kyø laø T1 , khi treo vaät m2 thì chu kyø laø T2.
** khi treo vaät coù khoái löôïng 21 mmm
+
=
thì chu kyø laø : 2
2
2
1
2TTT +=
** khi treo vaät coù khoái löôïng || 21 mmm
−
=
thì chu kyø laø : || 2
2
2
1
2TTT −=
12. Neáu caùc loø xo coù ñoä cöùng k1, k2…kn, coù chieàu daøi töï nhieân l1, l2, …ln coù baûn chaát gioáng nhau
hay ñöôïc caét töø cuøng moät loø xo ko, lo thì:
nnklklklkl
=
=
=
...
331100
13. Khoảng thời gian ngắn nhất để vật đi từ vị trí có toạ độ x1 đến x2
21
t
ϕ
ϕ
ϕ
ωω
−
Δ
Δ= = với
1
1
2
2
s
s
x
co
A
x
co
A
ϕ
ϕ
⎧=
⎪
⎪
⎨
⎪=
⎪
⎩
K2
K1
→
A
F →
B
F
→
P
m
A B
m
K2
K1
K
M
T/4
X
-A
T/6 T/12 T/12 T/6
T/4
0
-A/2 A/2
A
www.MATHVN.com
WWW.MATHVN.COM


















