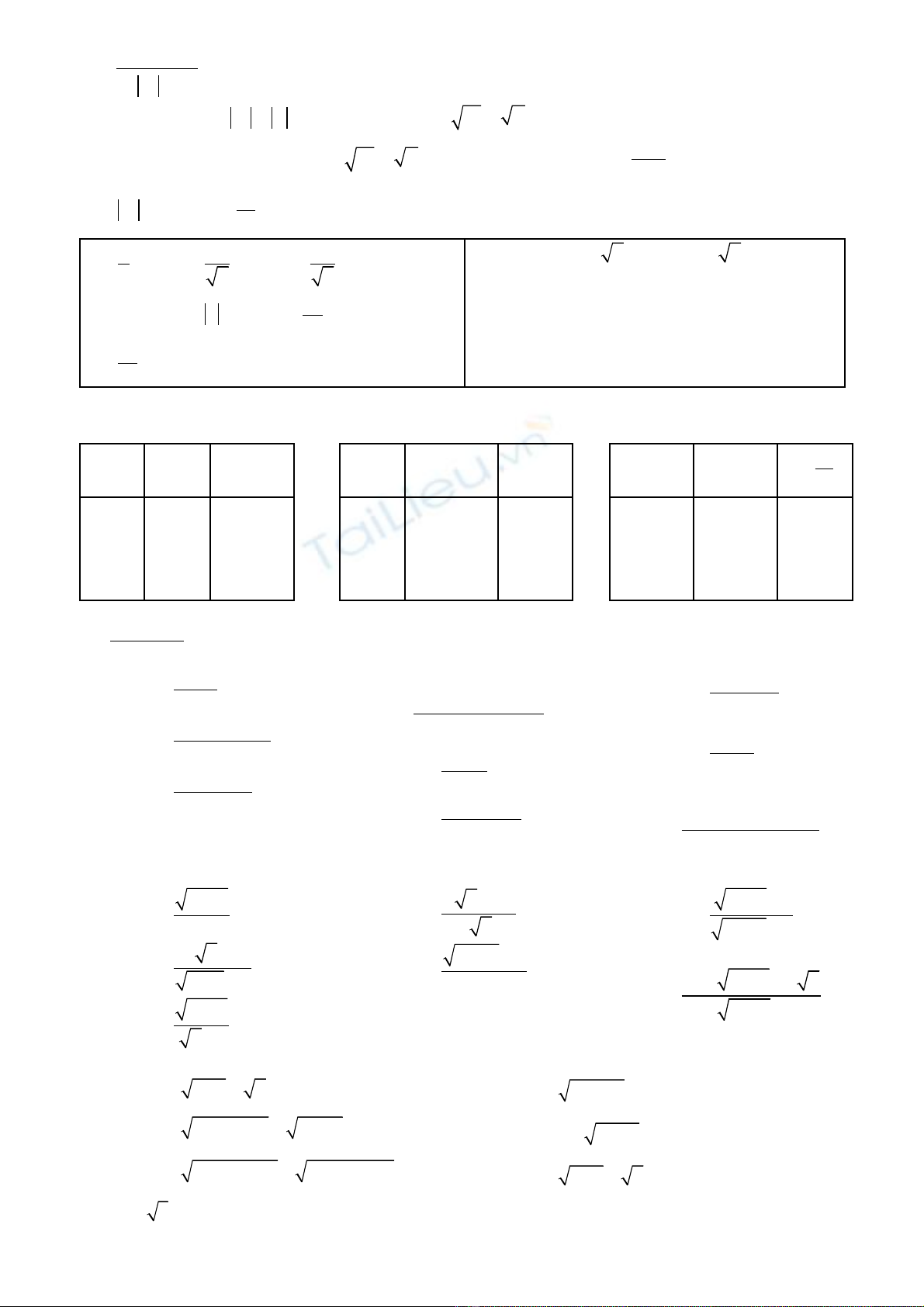
GI I H N DÃY SỚ Ạ Ố
A / Lý thuy tế:
•N u ế
,lim 0 lim 0
n n n n
u v n v u< ∀ = =�
•
lim c c
=
•
lim lim
n n
u L u L= =�
•
3
3
lim lim
n n
u L u L= =�
;
•
lim , 0 0,lim
n n n
u L u n L u L= > ∀ > =�
•
21
1 1 1
... 1
u
S u u q u q q
= + + + = −
•
1
lim lim 0
n
n
uu
= + =��
lim 0
n
q=
n u ế
1q<
*
1
lim 0,
k
k N
n=N
lim 0
k
c
n=
3
lim ; lim ; lim ; n n n= +n= + = +m
lim
n
q= +m
n u ế
1q>
;
*
lim ,
k
n k N= +N,
lim
n
u=im
,
lim
n
v=im
lim
n
u=im
,
lim 0
n
v L=L
lim 0
n
u L=L
,
lim 0
n
v=
lim
n
u
lim
n
v
lim .
n n
u v
lim
n
u
D u c a ấ ủ
L
lim .
n n
u v
D uấ
c a LủD uấ
c a ủ
n
v
lim
n
n
u
v
+i
+i
−i
−i
+i
−i
+i
−i
+i
−i
−i
+i
+i
+i
−i
−i
+
−
+
−
+i
−i
−i
+i
+
+
−
−
+
−
+
−
+i
−i
−i
+i
B/ Bài T p:ậ
Bài 1 tìm các gi i h n sau:ớ ạ
1.
2 1
lim 1
n
n
+
+
2.
2
2
3 4 1
lim 2 3 7
n n
n n
− + +
− +
3.
3
3
4
lim 5 8
n
n n
+
+ +
4.
( ) ( )
( )
3
2 1 3 2
lim 6 1
n n n
n
+ +
+
5.
2
1
lim 2
n
n
+
+
6.
2
4
lim 3 2
n
n n
+
− +
7.
( )
( )
3
2 1
lim 6 1
n n
n
+
+
8.
3
2
lim 1
n
n
+
+
9.
( )
( )
( )
2
3
2 1 3 2
lim 6 1
n n n
n
+ +
+
Bài 2 tìm các gi i h n sau:ớ ạ
1.
2
1
lim 2 3
n
n
+
+
2.
2 1
lim 2 2
n
n
+
+ +
ds2
3.
1
lim 1
n
n
+
+
ds1
4.
2
lim 1
n
n n
−
+ +
ds0
5.
33
2
lim 2
n n
n
+ +
+
ds1
6.
33
2
1 1
lim 3 2
n
n
+ −
+ −
7.
3
2 3
2
1
lim 1 3
n n n n
n n
+ + +
+ +
Bài 3 tìm các gi i h n sau: ớ ạ
1.
( )
lim 1n n+ −
ds0
2.
()
2 2
lim 5 1n n n n+ + − −
ds3
3.
()
2 2
lim 3 2 1 3 4 8n n n n+ − − − +
ds
3
4.
()
2
lim 4n n n− −
ds-2
5.
()
2
lim 3n n− +
ds0
6.
( )
lim 1n n+ +
- 1 -
7.
()
3 2 3
lim n n n− +
ds1/3
8.
( )
3 3
lim 1n n− +
ds0
9.
33
2
1
lim 1
n n
n n
+ −
+ −
10.
()
3 3 2 2
lim 3 1 4n n n n− + − +
Bài 4 tìm các gi i h n sau:ớ ạ
1.
1 4
lim1 4
n
n
−
+
2.
1
2
3 4
lim 3 4
n n
n n
+
+
−
+
3.
3 4 5
lim 3 4 5
n n n
n n n
− +
+ −
4.
1
1
264
lim 3 6
nnn
n n
+
+
+ −
+
5.
2
2
3 4 1
lim 2
n
n n
n
− + +
Bài 5 tìm các gi i h n sau:ớ ạ
1.
sin
lim 1
n
n
π
+
2.
2
sin10 cos10
lim 2
n n
n n
+
+
Bài 6 tìm các gi i h n sau:ớ ạ
1.
2
1 3 5 ... (2 1)
lim 3 4
n
n
+ + + + +
+
ds1/3
2.
2
1 2 3 ...
lim 3
n
n
+ + + +
−
ds1/2
3.
2 2 2 2
1 2 3 ...
lim ( 1)( 2)
n
n n n
+ + + +
+ +
ds1/3
4.
1 1 1
lim ...
1.2 2.3 ( 1)n n
� �
+ + +
� �
+
� �
ds1
5.
1 1 1
lim ...
1.3 3.5 (2 1)(2 1)n n
� �
+ + +
� �
− +
� �
Bài 7 Tính các t ng sau:ổ
1.
1 1
1 ...
2 4
S= + + +
2.
1 1 1
1 ...
3 9 27
S= − + − +
3.
2 3
1 0,1 (0,1) (0,1) ....S= + + + +
4.
2 3
2 0,3 (0,3) (0,3) ....S= + + + +
Bài 8:đ i s th p phân vô h n tu n hoàn ra phân s :ổ ố ậ ạ ầ ố
1. 1,1111….
2. 2,3333…
3. 0,2222…
4. 0,212121….
5. 0,23111…
- 2 -
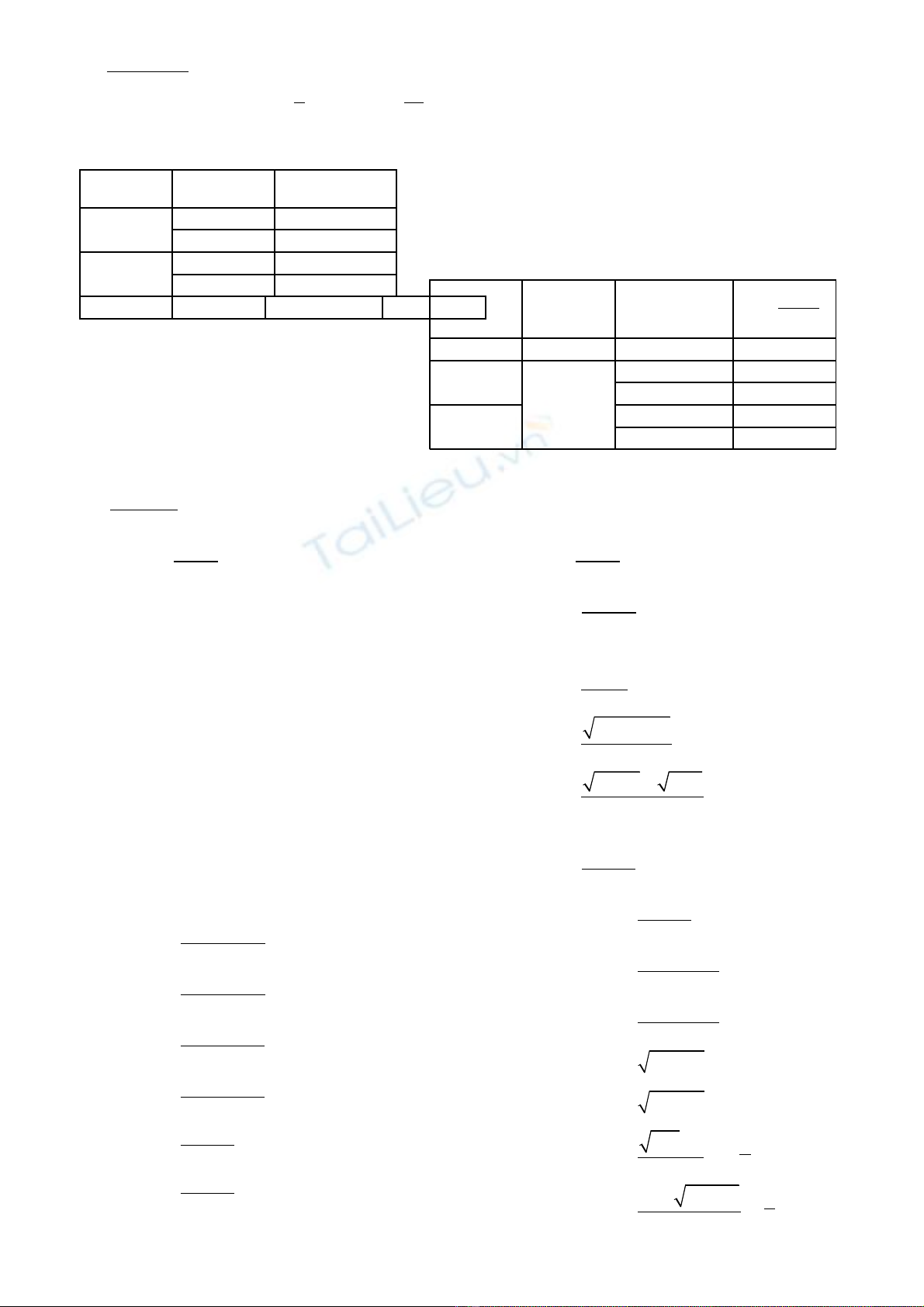
GI I H N HÀM SỚ Ạ Ố
A/Lý thuy tế :
0
0
lim
x x
x x
x
=
0
lim
x x
C C
C
=
1
lim 0
x
x
xim
=
1
lim 0
k
x
x
xim
=
lim
k
x
x
x+m
= +m
, 2
lim , 2 1
k
x
k l
xk l
k−,
+− =
+
==−− = +
−
( ) ( ) ( )
00 0
lim lim lim
x x x x x x
f x L f x f x L
− +
−−+
= = =�
( )
0
lim
x x
f x
f
( )
0
lim
x x
g x
g
( ) ( )
0
lim .
x x
f x g x
f
0L>
+x
+x
−x
−x
0L>
+x
−x
−x
+x
B/ Bài t p:ậ
Bài 1:Dùng đ nh nghĩa tính các gi i h n sau:ị ớ ạ
1.
2
3
9
lim 3
x
x
x
x
−
−
2.
( )
2
1
lim 3 1
x
x x
x
+ +
3.
2
3
9
lim 4
x
x
x
x
−
+
4.
2
2
2 9
lim 4
x
x
x
x+m
−
+
Bài 2 Tìm các gi i h n sau::ớ ạ
1.
2
lim
x
x
x
đs2
2.
( )
2
lim 3
x
x
x
+
đs5
3.
( )
2
2
lim 2 3 5
x
x x
x
− − +
đs-9
4.
( ) ( )
0
lim 3 2
x
x x
x
− +
đs-6
5.
1
5 2
lim 1
x
x
x
x
+
+
đs7/2
6.
2
2
3 1
lim 1
x
x x
x
x
+ −
−
đs3
7.
2
5 2 1
lim 1
x
x x
x
x
− + −
+
đs2/3
Bài 3:Tìm các gi i h n sau:ớ ạ
1.
( )
3
lim 2
x
x x
x+m
+
đs
+
2.
( )
3
lim 2
x
x x
x−m
+
đs
−s
3.
2
2
5 3 1
lim 2 3
x
x x
x
x+m
+ +
+
đs5/2
4.
2
2
5 3 1
lim 2 3
x
x x
x
x−m
+ +
+
đs5/2
5.
4 2
4
5 1
lim 2 3
x
x x
x
x+m
+ +
+
đs1/2
6.
4 2
4
5 1
lim 2 3
x
x x
x
x−m
+ +
+
đs1/2
7.
2
3 1
lim 2 3
x
x
x
x+m
+
+
đs0
8.
2
3 1
lim 2 3
x
x
x
x−m
+
+
đs0
9.
2
3
3 1
lim 2 5
x
x
x
x+m
+
+
đs0
10.
2
3
3 1
lim 2 5
x
x
x
x−m
+
+
đs0
11.
2
2 2
lim 1
x
x x
x
x+m
+ +
+
đs
+s
12.
2
2 2
lim 1
x
x x
x
x−m
+ +
+
đs
−s
13.
2
lim 2
x
x x
x+m
+
đs
+
14.
2
lim 2
x
x x
x−m
+
đs
+
15.
2
4 1
lim 3 1
x
x
x
x1m
+
−
đs
2
3
3
16.
4
2
3 5
lim 2 4 5
x
x x x
x x
xxx
+ −
+ −
đs
1
2
- 3 -
( )
0
lim
x x
f x
f
( )
0
lim
x x
g x
g
D u c aấ ủ
g(x)
( )
( )
0
lim
x x
f x
g x
g
L
Lx
Tuỳ ý 0
L>0
0
+
+>
-
−>
L<0 +
−<
-
+<
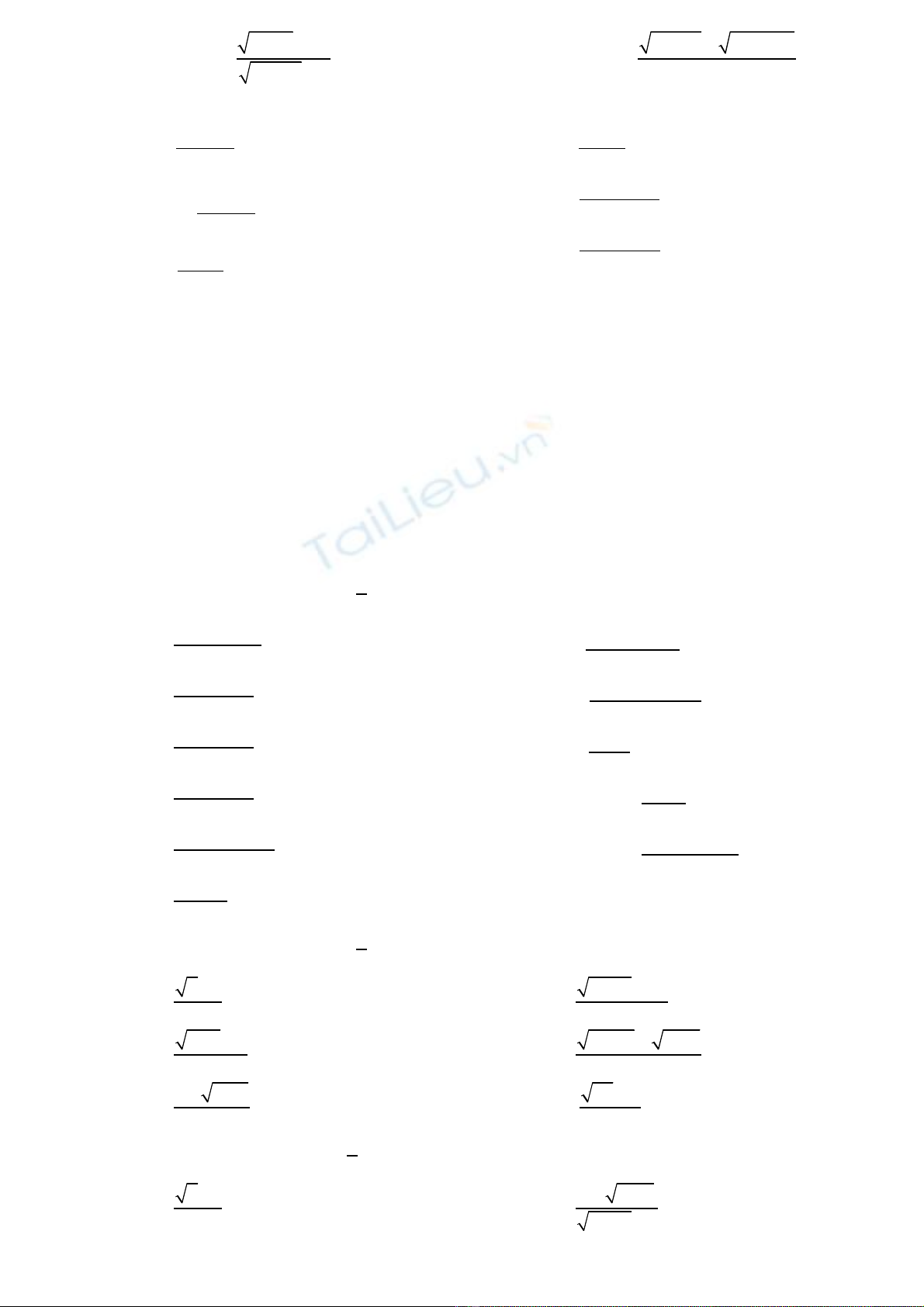
17.
2
2
3 4
lim 4 1
x
x x
x x
xxm
+ +
+ −
đs5 , -1 18.
2 2
9 1 4 2
lim 1
x
x x x
x
xxx
+ − +
+
đs
11
Bài 4 Tìm các gi i h n sau::ớ ạ
1.
( )
2
3
5 2
lim 3
x
x
x
x
+
−
đs
+s
2.
( )
2
3
2 3
lim 3
x
x
x
x
� �
+
−
� �
−
� �
� �
đs
−s
3.
3
5 2
lim 3
x
x
x
−
−
+
−
đs
−s
4.
3
5 2
lim 3
x
x
x
+
+
+
−
đs
+s
5.
2
2
5 2
lim 2
x
x x
x
−
−
+ +
−
đs
−s
6.
2
2
5 2
lim 2
x
x x
x
+
+
+ +
−
đs
+s
Bài 5 Tìm các gi i h n sau::ớ ạ
Cho hàm s :ố
( )
2
2 3 1 , 2
3 7 , 2
x x x
f x x x
x+ −x
==+ <
+
Tìm các gi i h n sau:ớ ạ
1.
( )
1
lim
x
f x
f
2.
( )
3
lim
x
f x
f
3.
( )
2
lim
x
f x
f
Bài 6 Tìm các gi i h n sau::ớ ạ
Cho hàm s :ố
( )
2
1 2 , 1
5 4 , 1
x x
f x x x
x− <
==+<
+
Tìm các gi i h n sau:ớ ạ
1.
( )
0
lim
x
f x
f
2.
( )
3
lim
x
f x
f
3.
( )
1
lim
x
f x
f
Bài 7 Tìm các gi i h n sau::(d ng ớ ạ ạ
0
0
)
1.
2
3
2 15
lim 3
x
x x
x
x
+ −
−
đs8
2.
2
2
1
2 3
lim 1
x
x x
x
x
+ −
−
đs2
3.
2
2
2
3 2
lim 2
x
x x
x x
x
− +
−
đs1/2
4.
2
2
2
3 2
lim 6
x
x x
x x
x
− +
+ −
đs1/5
5.
3 2
2
1
1
lim 3 2
x
x x x
x x
x
− − +
− +
đs0
6.
4 4
lim
x a
x a
x a
x
−
−
đs4a3
7.
( )
22
0
lim
h
x h x
h
h
+ −
đs2x
8.
4 2
3 2
3
6 27
lim 3 3
x
x x
x x x
x−
− −
+ + +
đs-36/5
9.
5
3
1
1
lim 1
x
x
x
x−
+
+
đs5/3
10.
1
1
lim 1
m
n
x
x
x
x
−
−
đsm/n
11.
( )
6 5
2
1
4 5
lim 1
x
x x x
x
x
− +
−
đs10
Bài 8 Tìm các gi i h n sau::(d ng ớ ạ ạ
0
0
)
1.
1
1
lim 1
x
x
x
x
−
−
đs1/2
2.
2
3
1 2
lim 9
x
x
x
x
+ −
−
đs1/24
3.
2
1
2 3
lim 1
x
x
x
x
− +
−
đs-1/8
4.
2
2
4 1 3
lim 4
x
x
x
x
+ − −
−
đs1/6
5.
2
2
2 5 7
lim 2
x
x x
x x
x
+ − +
−
đs1/12
6.
3
2
4 2
lim 2
x
x
x
x−
+
+
đs1/3
Bài 9Tìm các gi i h n sau:(d ng ớ ạ ạ
0
0
)
1.
3
2
1
1
lim 1
x
x
x
x
−
−
đs1/6 2.
2
2
lim 4 1 3
x
x x
x
x
− +
+ −
đs9/8
- 4 -
3.
3
0
1 1
lim 3
x
x
x
x
− −
đs1/9
4.
3
2
1
1
lim 3 2
x
x
x
x−
+
+ −
đs-2/3
5.
3
1
7 2
lim 1
x
x
x
x
+ −
−
đs1/2
6.
3
1
1
lim 1
x
x
x
x
−
−
đs2/3
7.
3
0
1 1
lim
x
x x
x
x
+ − −
đs5/6
8.
0
1 4 3
lim
x
x x
x
x
+ + + −
9.
0
9 16 7
lim
x
x x
x
x
+ + + −
10.
( )
323
2
1
2 1
lim 1
x
x x
x
x
− +
−
Bài 10:Tìm caùc giôùi haïn sau
1.
()
2
lim
x
x x x
x+x
+ −
2.
()
2
lim 2 1 4 4 3
x
x x x
x+x
− − − −
3.
()
2 2
lim 1 1
x
x x x x
x+x
− + − + +
4.
()
3 3
lim 1
x
x x
x+m
+ −
5.
+∞→
x
lim
(
xxx 5
2
+−
) (Ñs:-5/2)
6.
−∞→
x
lim
(
1
22
+−−
xxx
) (Ñs:1/2)
7.
()
32 3
lim . 1
x
x x x
x+x
+ −
8.
()
3 33 2 3
lim 5 8
x
x x x x
x+x
+ − +
Bài 11:Tìm caùc giôùi haïn sau
1.
2
1
2 1
lim 1 1
x
x x
x
� �
−
� �
− −
� �
2.
3
1
1 3
lim 1 1
x
x x
x
� �
−
� �
− −
� �
3.
2 2
1
1 1
lim 3 2 5 6
x
x x x x
x
� �
−
� �
− + − +
� �
BAØI 3: HAØ M SOÁ LIEÂN TUÏC
Bài 1: Xeùt tí nh li eân tuï c cuûa haøm soá t aï i ñi eåm x0
1. f(x) =
2
9 3
3
6 3
xkhi x
x
khi x
k−−
−−
−
−=
=
tại x0=3
2. f(x) =
2
25 5
5
9 5
xkhi x
x
khi x
k−−
−−
−
−=
=
tại x0=5
3.
( )
2 3
2
2 7 5 khi 2
3 2
1 khi 2
x x x x
f x x x
x
x− + − −
−
=− +
−
−=
=
tạix0=2
4.
( )
3
3
2 khi 1
1
4 khi 1
3
x x x
x
f x
x
x+ + + −
+
++
==
== −
=
=
tại x0= -1
5.
( )
1 2 3 khi 2
2
1 khi 2
xx
f x x
x
x− − −
−
==−
−=
=
tại
x0=2
6.
( )
3
3 2 2 khi 2
2
3 khi 2
4
xx
x
f x
x
x+ − +
+
+−
==
==
=
=
tại
x0=2
7.
( )
2 khi 4
5 3
3 khi 4
2
xx
x
f x
x
x−−
−
−+ −
==
==
=
=
tại x0=4
8.
( )
2
+4 2
2 1 2
x khi x
f x x khi x
x<
==+k
+
tại x0=2
9.
( )
4 2
1 1
3 2 1
x x khi x
f x x khi x
x+ −h−
==+ > −
+
tại x0= -
1
10.
( )
2
0
1 0
x khi x
f x
x khi x
x<
<
==−k
−
−
tại
x0=0
11.
( )
5khi 5
2 1 3
3 khi 5
2
xx
x
f x
x
−
−>
>
>− −
==
==
=
=
tại
x0=5
12.
( )
3 2
2 1
2
x x
f x x
+ −
=−
tại x0=2
13. f(x)=
5
1
4
−
++
x
xx
tại x0 = 5
- 5 -