CHƯƠNG I
CẤU TẠO NGUYÊN TỬ
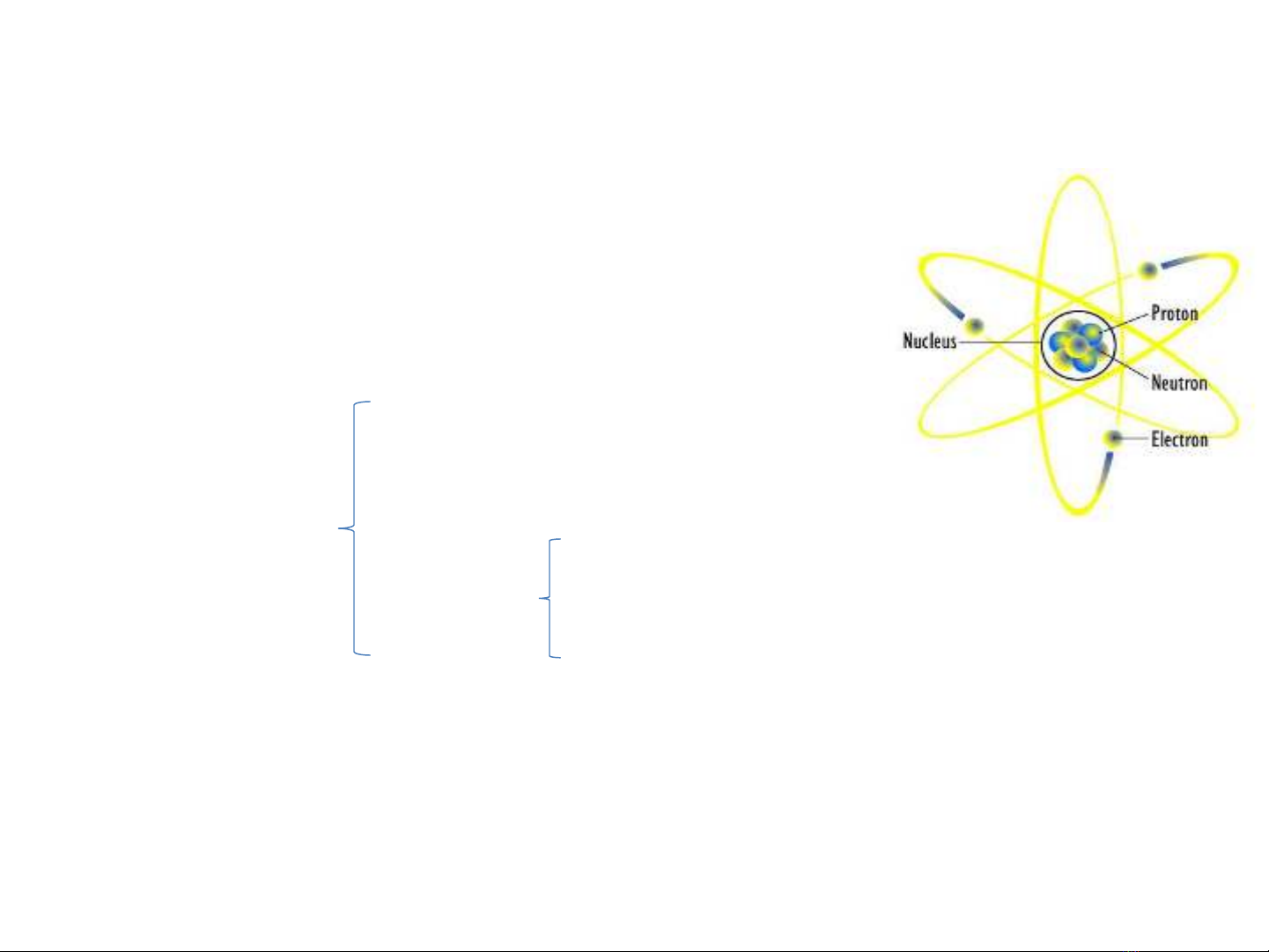
I. Các cấu tử chánh:
1. Các hạt cơ bản:
Nguyên tử Electron(e) -1
Nhân Proton(p) +1 1dvc
Neutron(n) 0 1dvc
me/mp = 1/1840 Kl(ng.t) = Kl(nhân)

2. Ký hiệu nguyên tử:
Z: Bậc số ng.tử= ∑p trong nhân
A= Số khối = ∑p + ∑n
∑p = 6
∑n = 12 – 6 = 6
Nguyên tử ở trạng thái cơ bản trung
hòa điện
∑e = ∑p =6
X
A
Z
C
12
6
3. Ng.tử đồng vị:
1 protn. Có 0; 1; 2
neutron
6 proton. Có 6; 7; 8
neutron
17 proton. có 18; 19; 20
neutron
Các ng.t đồng vị có cùng Z ∑e bằng
nhau hóa tính giống nhau.
H
1
1
H
2
1
H
3
1
C
12
6
C
13
6
Cl
35
17
Cl
37
17
Cùng Z, khác A
4. Nguyên tố – nguyên tử:
*1 ng.tố x.định khi có 1 giá trị Z x.định.
*Trong 1 ng.tố có thể gồm nhiều ng. tử
đồng vị với thành phần xác định
*1H gồm: 1H(99,985%) và 2H(0,015%)
*17Cl gồm: 35Cl(75,4%) và 37Cl(24,6%)
*6C gồm: 12C(98,982%) và 13C(1,108%)
*Klnt (ng.tố) =
Td: klnt(Cl) =
100
).%(iA
i
∑
453,35
100
6,24.374,75.35
=
+

II. Cấu tạo ng.tử theo thuyết cơ lượng tử.
e di chuyển trên các orbital ng.tử (AO)
* Về ph.d vật lý:AO:vùng k.g quanh nhân
trên đó x.s tìm thấy e cực đại từ 90→99%
*Về ph.d toán học: AO được biểu diễn bởi
hàm số Ѱn,l,m :nghiệm của p.t Schrodinger
∂2 Ѱ ∂2 Ѱ ∂2 Ѱ 8π2m
── + ── + ── + ─── (E – V) Ѱ = 0
∂x2 ∂y2 ∂z2 h2
Giải p.t này các cặp nghiệm E; Ѱ


























