"Bài giảng Cấu trúc dữ liệu và giải thuật – Bài 6: Sắp xếp nhanh - Quick Sorts" trình bày thuật toán QuickSort, ví dụ về QuickSort, hoạt động của QuickSort, hiệu quả của QuickSort. Mời các bạn cùng tham khảo bài giảng để nắm chi tiết nội dung kiến thức.
AMBIENT/
Chủ đề:
Nội dung Text: Bài giảng Cấu trúc dữ liệu và giải thuật – Bài 6: Sắp xếp nhanh - Quick Sorts
- Cấu trúc dữ liệu và giải thuật
Bài 6. Sắp xếp nhanh - Quick Sorts
Lecturer: PhD. Ngo Huu Phuc
Tel: 0438 326 077
Mob: 098 5696 580
Email: ngohuuphuc76@gmail.com
1 Ngo Huu Phuc, Le Quy Don Technical University
- Bài 6. Quick Sorts
Nội dung:
6.1. Thuật toán QuickSort (6)
6.2. Ví dụ về QuickSort (7)
6.3. Hoạt động của QuickSort (6)
6.4. Hiệu quả của QuickSort (6)
Tham khảo:
1. Intro to Algorithms Chapter 8 QuickSort.htm
2. Lecture 5 – quicksort.htm
3. Quick Sort.htm
4. Bài giảng của TS Nguyễn Nam Hồng
2 Ngo Huu Phuc, Le Quy Don Technical University
- 6.1. Thuật toán QuickSort (1/6)
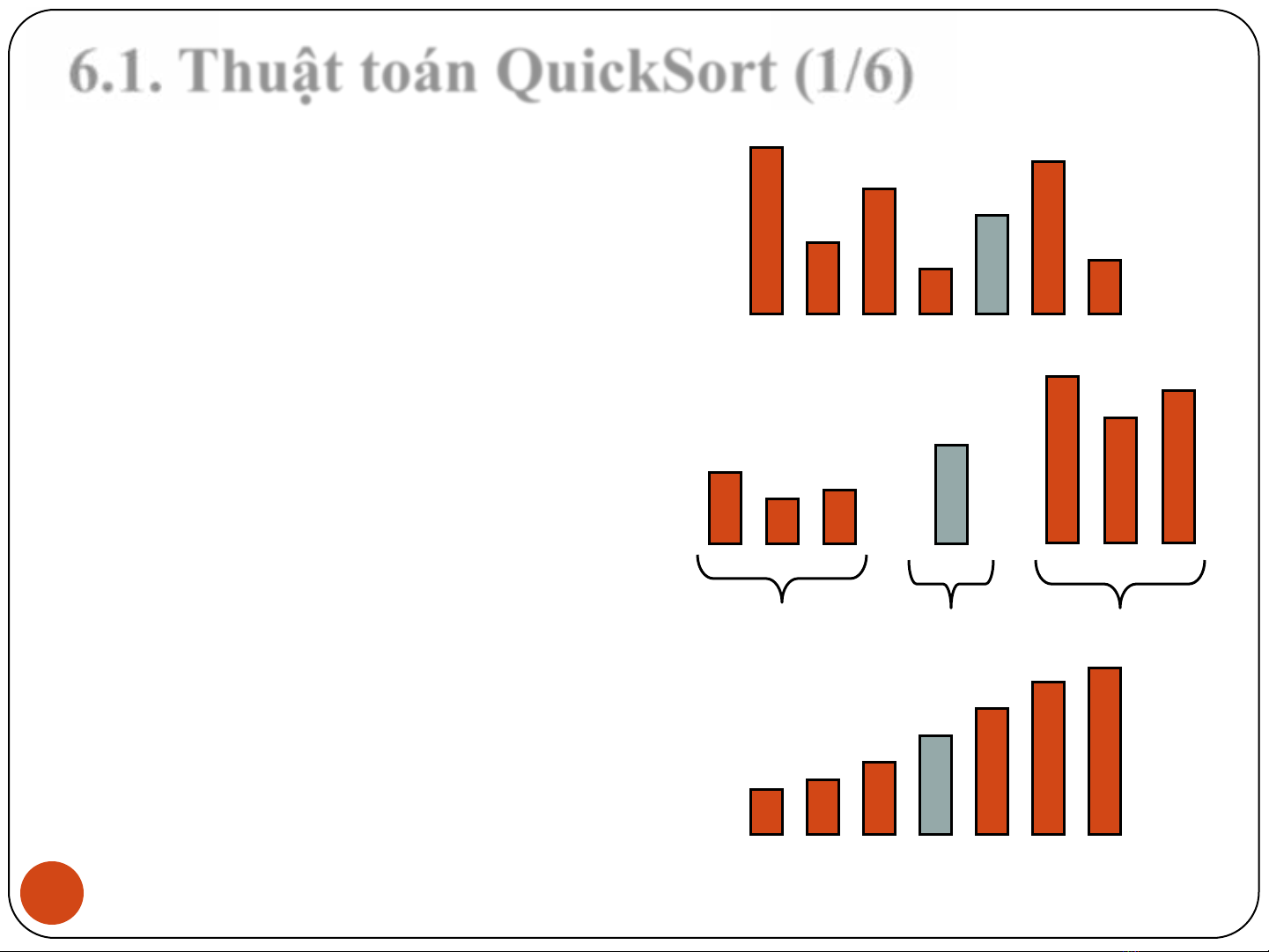
Giải thuật Quick-sort là
phương pháp sắp xếp dựa
trên chiến lược chia để trị. x
Giải thuật gồm các bước:
Phép chia: chọn ngẫu nhiên
một phần tử x làm khóa,
chia tập dữ liệu S ban đầu
thành 3 phần: x
L chứa các phần tử nhỏ hơn x
E chứa các phần tử bằng x L E G
G chứa các phần tử lớn hơn x
Bước lặp: sắp xếp 2 tập L
và G
Hiệu chỉnh lại các tập L, E x
và G
3 Ngo Huu Phuc, Le Quy Don Technical University
- 6.1. Thuật toán QuickSort (2/6)
Các bước cơ bản của thuật toán:
Chia tập dữ liệu ban đầu thành 2 tập con:
sao cho, tất cả các phần tử bên trái nhỏ hơn tất
cả các phần tử bên phải.
Sắp xếp 2 tập con một cách độc lập và nối chúng
lại với nhau:
như vậy, ta được dãy đã sắp xếp.
4 Ngo Huu Phuc, Le Quy Don Technical University
- 6.1. Thuật toán QuickSort (3/6)
Với mỗi tập con trên, mỗi tập chia thành 02 tập
con nếu có thể
như vậy, ta có tối đa 04 tập con.
tập các phần tử nhỏ nhất ở bên trái cùng, tập
các phần tử lớn nhất ở bên phải cùng.
Lặp lại quá trình trên cho đến khi tập chỉ có 1
phần tử
nối tất cả các tập với nhau ta được dãy đã sắp
xếp.
5 Ngo Huu Phuc, Le Quy Don Technical University
- 6.1. Thuật toán QuickSort (4/6)
Ta chia t ập dữ liệu ban đầu như sau:
Trên tập S, lấy mỗi phần tử y được lấy ra khỏi
tập
Đưa phần tử y vào tập L, E hay G, tùy thuộc
vào phép so sánh với khóa x
Với mỗi phép lấy 1 phần tử và đưa chúng vào tập
tương ứng, độ phức tạp của phép toán đó là
O(1).
Như vậy, phép chia dữ liệu của thuật toán
QuickSort có độ phức tạp O(n).
6 Ngo Huu Phuc, Le Quy Don Technical University
- 6.1. Thuật toán QuickSort (5/6)
7 4 9 6 2 → 2 4 6 7 9
4 2 → 2 4 7 9 → 7 9
2→2 9→9
7 Ngo Huu Phuc, Le Quy Don Technical University
- 6.1. Thuật toán QuickSort (6/6)
Việc thực thi giải thuật
QuickSort được mô tả qua
cây nhị phân:
Mỗi node biểu diễn một
lần gọi đệ quy và lưu giữ:
Dãy chưa được sắp xếp và
khóa.
Dãy sau khi sắp xếp.
Gốc của cây là lần gọi đệ
quy đầu tiên.
Các lá của cây là lần gọi
ứng với dãy con có kích
thước 0 hoặc 1.
8 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (1/7)
Chọn khóa
9 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (2/7)
Phân chia dãy ban đầu bằng gọi đệ quy với khóa đã chọn.
10 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (3/7)
Gọi đệ quy cho dãy con, với khóa mới
11 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (4/7)
Tương tự, gọi đệ quy, sau đó nối kết quả.
12 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (5/7)
Tương tự cho phần bên phải.
13 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (6/7)
Gọi đệ quy cho dãy con, với khóa mới
14 Ngo Huu Phuc, Le Quy Don Technical University
- 6.2. Ví dụ về QuickSort (7/7)
Nối kết quả cho gốc của cây.
15 Ngo Huu Phuc, Le Quy Don Technical University
- 6.3. Hoạt động của QuickSort (1/6)
Có thể mô tả như sau:
Với tập ban đầu, chọn 1 phần tử làm khóa.
Đổi chỗ phần tử đầu tiên với khóa.
Sử dụng 2 chỉ số i và j để duyệt phần còn lại trên dãy.
Chỉ số i tăng đến khi tại vị trí i đó, phần tử này có giá trị lớn hơn
khóa. Chỉ số j giảm đến khi giá trị tại vị trí j nhỏ hơn khóa.
So sánh giữa i và j, nếu i
- 6.3. Hoạt động của QuickSort (2/6)
Chọn khóa:
Ta có th ể chọn bất kỳ phần tử nào trong mảng làm khóa.
Nếu chọn phần tử đầu tiên của mảng làm khóa, lựa chọn này là tồi
nếu mảng đã sắp xếp. Khi đó, một mảng con có 0 phần tử. Thông
thường, chọn khóa gần với giữa của mảng với hi vọng lựa chọn này
sẽ cho 2 mảng con có số phần tử gần bằng nhau.
Hàm chọn vị trí có dạng: Việc chọn này cũng tùy ý, có
int getkeyposition(int i,int j) thể sử dụng hàm random để
chọn khóa. Hàm này có dạng:
{
int getkeyposition(int i, int j)
return(( i+j )/ 2);
{
}
return(random number in the
range of i to j);
}
17 Ngo Huu Phuc, Le Quy Don Technical University
- 6.3. Hoạt động của QuickSort (3/6)
Xây dựng hàm đệ quy:
Hàm đệ quy cho giải thuật có thể gọi
QSort(S, a, b)
sắp dãy con trong dãy ban đầu S tử chỉ số a đến
chỉ số b.
Với QSort(L, 0, n-1) sắp mảng L từ phần tử
đầu tiên đến phần tử cuối n-1.
QSort(S, a, b) sẽ được gọi đệ quy cho các
mảng con nhỏ hơn, với chỉ số thay đổi.
18 Ngo Huu Phuc, Le Quy Don Technical University
- 6.3. Hoạt động của QuickSort (4/6)
Chia dữ liệu:
Với khóa đã chọn x
Tổ chức lại tập S sao cho:
S[a]…S[t-1] là các phần tử < x
S[t] = x
S[t+1]…S[b] là các phần tử > p
19 Ngo Huu Phuc, Le Quy Don Technical University
- 6.3. Hoạt động của QuickSort (5/6)
#include "stdio.h" void inputdata(int list[],int n)
#include "conio.h" {
#define MAX 100 int i;
void swap(int *x,int *y);
printf("Nhap cac phan tu cho mang\n");
int getkeyposition(int i,int j);
for(i=0;i
Thêm vào BST
Báo xấu
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
