Bài giảng Chương 3: Bài toán đếm

Chia sẻ: Trung Trung | Ngày: | Loại File: PPTX | Số trang:11

Thêm vào BST

Báo xấu

181
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Chương 3: Bài toán đếm trình bày giới thiệu bài toán, nguyên lý bù trừ, hệ thức truy hồi, hàm sinh và bài toán đếm, định nghĩa hàm sinh, bài tập,... Mời các bạn cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Chương 3: Bài toán đếm

Chương 3 – Bài toán đếm 3.1. Giới thiệu bài toán 3.2. Nguyên lý bù trừ 3.3. Hệ thức truy hồi 3.4. Hàm sinh và bài toán đếm 3.5. Bài tập
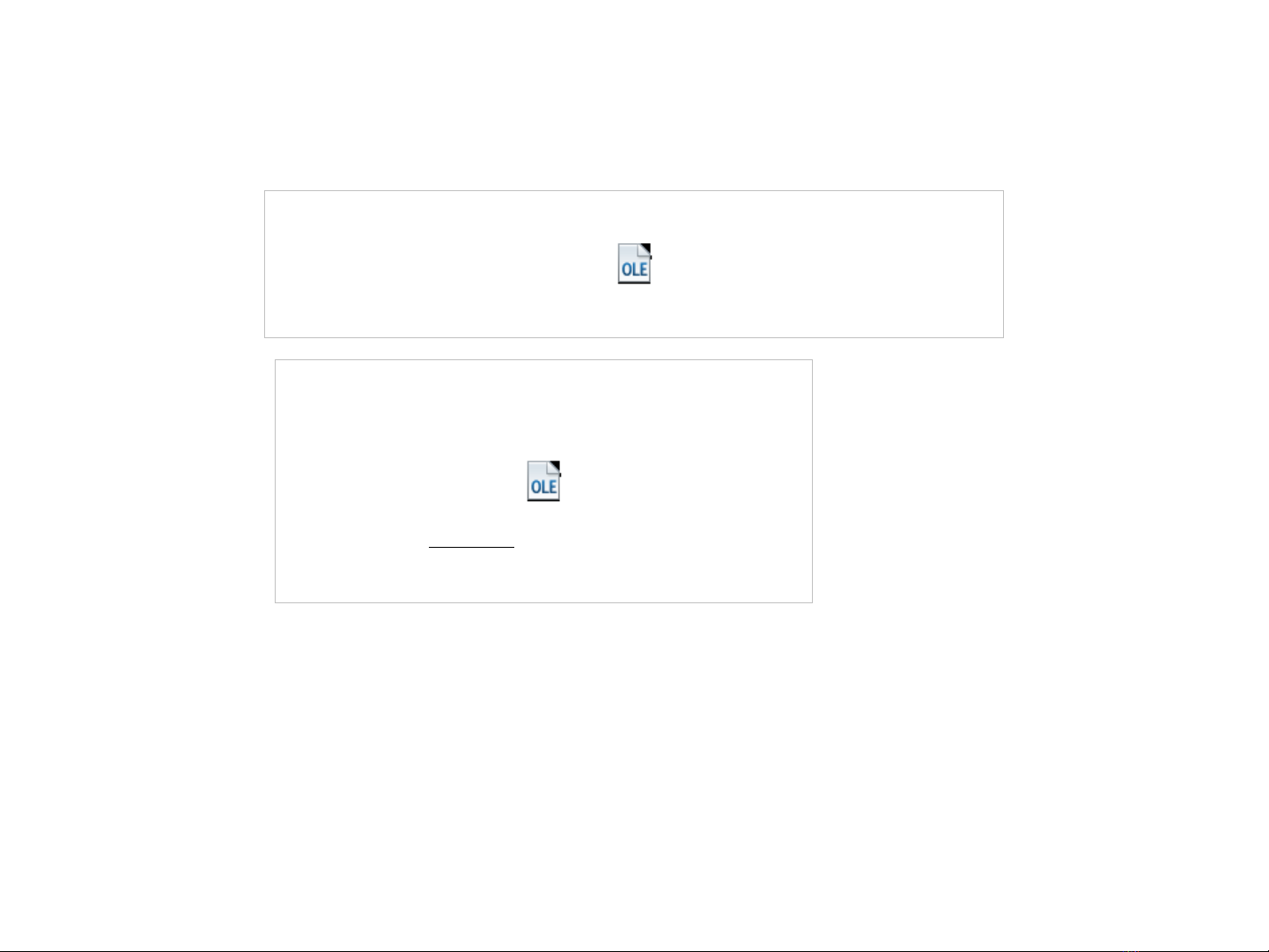
Định nghĩa hàm sinh • Định nghĩa: Hàm sinh g(x) của dãy số {hn | n = 0,1,2,…} là đa thức g ( x ) = h0 + h1 x + h2 x + ... = 2 i hi x i =0 m g1 ( x ) = ( 1 + x ) = m Cmk x k k =0 • Ví dụ 1: 1 g2 ( x ) = = 1 + x + x 2 + ... 1− x – g1(x) là hàm sinh của dãy tổ hợp hk = C(m,k) – g2(x) là hàm sinh của dãy hk = 1
Định nghĩa hàm sinh • Ví dụ 2: Xét hàm sau: k 1 �1 � � = ( 1 + x + x + ... ) k g( x) = =� 2 (1 − x ) k 1− x � � g(x) là hàm sinh của dãy hn (hệ số của số hạng xn ) t1 + t2 + ... + tk = n hn là số nghiệm nguyên không âm của phương trình: � hn = Rk n
1 = ( 1 + x + x + x + ... ) = 2 3 k n n R x (1 − x) k k n =0 1 = ( 1 + rx + r x + r x + ... ) = 2 2 3 3 k n n n R r x ( 1 − rx ) k k n =0 k x = x ( 1 + x + x + x + ... ) = x + x + x + ... k 2 3 k k +1 k +2 1− x k +1 1− x = 1 + x + ... + x k 1− x 1 = 1 + x + x + .... k 2k 1− x k x k +1 2 k +1 = x+x +x + .... 1− x k
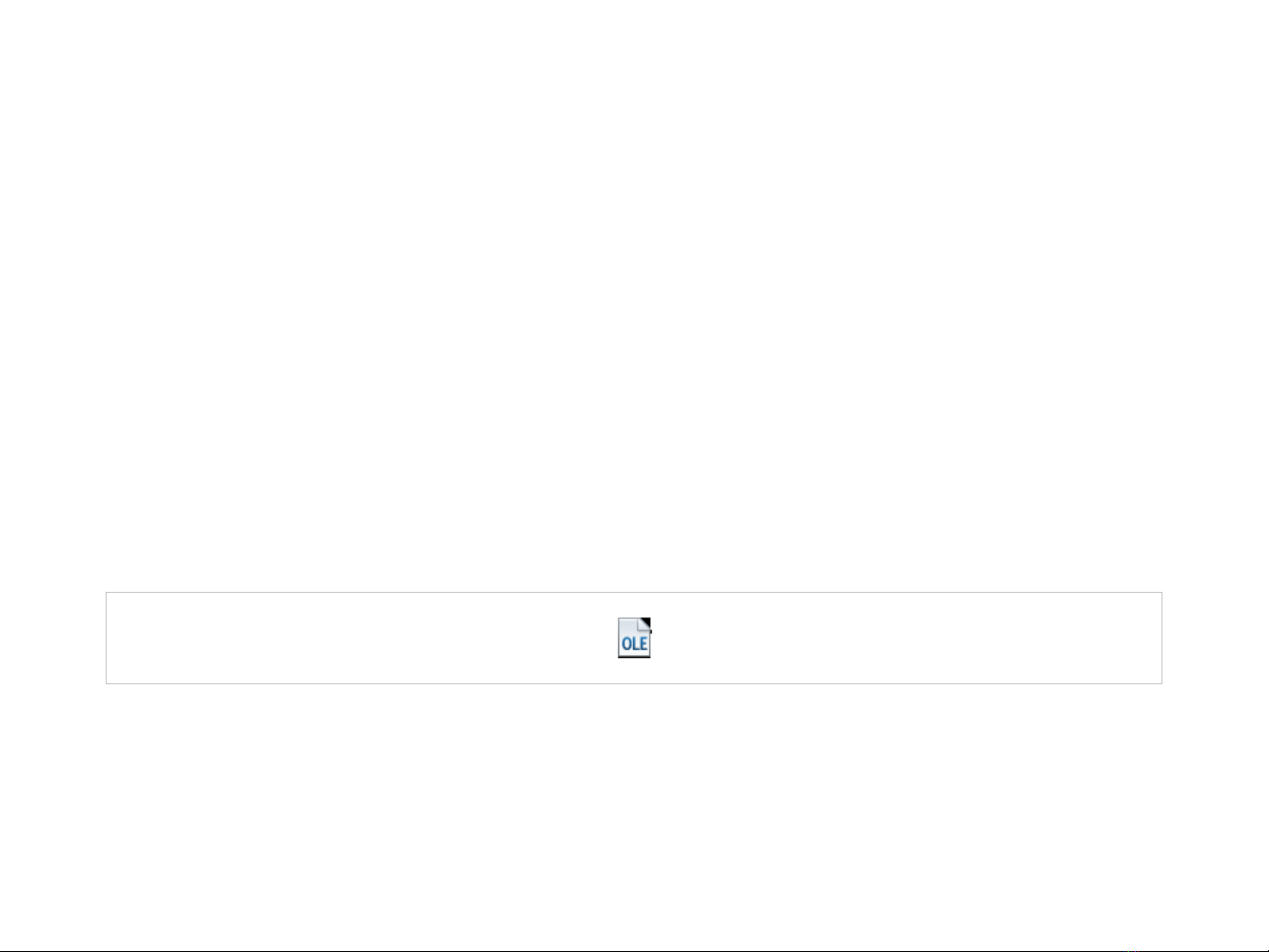
Hàm sinh và bài toán đếm • Ví dụ 3: Phương trình: x1 + x2 + x3 + x4 = 29 có bao nhiêu nghiệm nguyên không âm thỏa mãn: x1
Hàm sinh và bài toán đếm • Ví dụ 4: Phương trình: x1 + x2 + x3 + x4 = 29 có bao nhiêu nghiệm nguyên không âm thỏa mãn: x1
Hàm sinh và bài toán đếm • Ví dụ 5: Có bao nhiêu cách chọn ra n quả từ 4 loại quả: táo, chuối, cam, đào (mỗi loại đều có số lượng ít nhất là n) mà trong đó có số chẵn quả táo, số chuối chia hết cho 5, không quá 4 quả cam và không quá 1 quả đào? • Lời giải: – Gọi hn là số cách chọn thỏa mãn yêu cầu đề bài. –g (Khi ( x ) = đó 1 + xhàm 2 sinh + x4 + )( của1 +dãy x 6 + .... x 5 + hn x10 +có ... dạng:)( 1 + x + x2 + x3 + x4 ( 1 + x ) ) 1 1 1 − x5 1 = (1+ x + x + ... ) 2 = ( 1 + x) = 2 ( ) 2 1− x 1− x 1− x 2 5 1 − x hn = R = C n n = ( n + 1) ! = n +1 2 n + 2 −1 n !1!
Hàm sinh và công thức truy hồi • Ví dụ 6: Giải công thức truy hồi: an = 4 an − 2 a0 = 0; a1 = 1 • Lời giải: – Gọi g(x) là hàm sinh của dãy số thỏa mãn hệ thức truy hồi g ( x ) = a 0 + a1 x + a 2 x 2 + a 3 x 3 + ... – Ta có: = a0 + a1 x + 4a0 x 2 + 4a1 x 3 + ... = x + 4 x 2 g ( x) x 1 1 1 �n g ( x) = = 4 − 4 a n = 2 − ( −2 ) � n 1 − 4 x2 1 − 2 x 1 + 2 x 4� �
Hàm sinh và công thức truy hồi • Ví dụ 5: Giải công thức truy hồi: a0=1 , a1= 2 và an = 3an-1 - 2an-2 + 2 • Lời giải: – Gọi g(x) là hàm sinh của2 dãy3 số thỏa mãn hệ thức g ( x ) = a0 + a1 x + a2 x + a3 x + ... truy hồi g ( x ) = a0 + a1 x + ( 3a1 − 2a0 + 2 ) x 2 + ( 3a2 − 2a1 + 2 ) x 3... – Ta có: = 1 + 2 x − 3x + 3x ( a0 + a1 x + a2 x + a3 x + ...) − 2 x ( a0 + a1 x + a2 x + a3 x + ...) 2 3 2 2 3 +2 x 2 (1 + x + x 2 + ...) 2 2 x = 1 − x + 3xg ( x ) − 2 x 2 g ( x ) + 1− x 1− x 2x2 1 − 2 x + 3x 2 g ( x) = + = an = ? 1 − 3x + 2 x 2 ( 1 − x ) ( 1 − 3x + 2 x ) ( 1 − x ) 2 ( 1 − 2 x ) 2
Bài tập Sử dụng hàm sinh để giải các bài toán sau: Bài 1: BPT: x1 + x2 + x3 + x4 + x5 +x6 ≤n có bao nhiêu nghiệm nguyên không âm thỏa mãn: • x3 ≤ 3 và x4 chia hết cho 4 dư 2. • x2 < 2 và x5 lẻ Bài 2: Giải hệ thức truy hồi: a0 = 3; a1 = 4; an = 5an −1 − 6an − 2 + 7 n ( n 2)
Bài tập BPT: x1 + x2 + x3 + x4 + x5 +x6 ≤n có bao nhiêu nghiệm nguyên không âm thỏa mãn: • x3 ≤ 3 và x4 chia hết cho 4 dư 2. • x2 < 2 và x5 lẻ